Definition
Definition of Continuity
A function \( f(x) \) is said to be continuous at a point \( a \) in its domain if the limit of \( f(x) \) as \( x \) approaches \( a \) exists and is equal to \( f(a) \). That is,
This condition ensures that the function does not have any abrupt jumps, holes, or breaks at \( x = a \). More explicitly, continuity at \( a \) requires the following three conditions to hold:
- \( f(a) \) is defined, meaning \( a \) belongs to the domain of \( f(x) \).
- The limit \( \lim\limits_{x \to a} f(x) \) exists, meaning the left-hand limit and right-hand limit at \( x = a \) are equal.
- The limit equals the function value, i.e., \( \lim\limits_{x \to a} f(x) = f(a) \).
If any of these conditions fail, the function is discontinuous at \( x = a \).
Consider the function \( f: \mathbb{R} \to \mathbb{R} \), defined as:
We will check if \( f(x) \) is continuous at \( x = 0 \). According to the definition of continuity at a point, \( f(x) \) is continuous at \( x = 0 \) if
Step 1: Evaluate \( f(0) \)
From the given function definition,
Step 2: Evaluate \( \lim\limits_{x \to 0} f(x) \)
Since \( f(x) = \frac{\sin x}{x} \) when \( x \neq 0 \), we need to find
This is a standard limit, and it is well-known that
Step 3: Check the continuity condition
Now, compare the limit value with \( f(0) \):
Since the limit exists and equals the function value at \( x = 0 \), \( f(x) \) is continuous at \( x = 0 \).
Thus, the function \( f(x) \) satisfies the continuity condition at \( x = 0 \), and hence, \( f(x) \) is continuous at this point.
Example
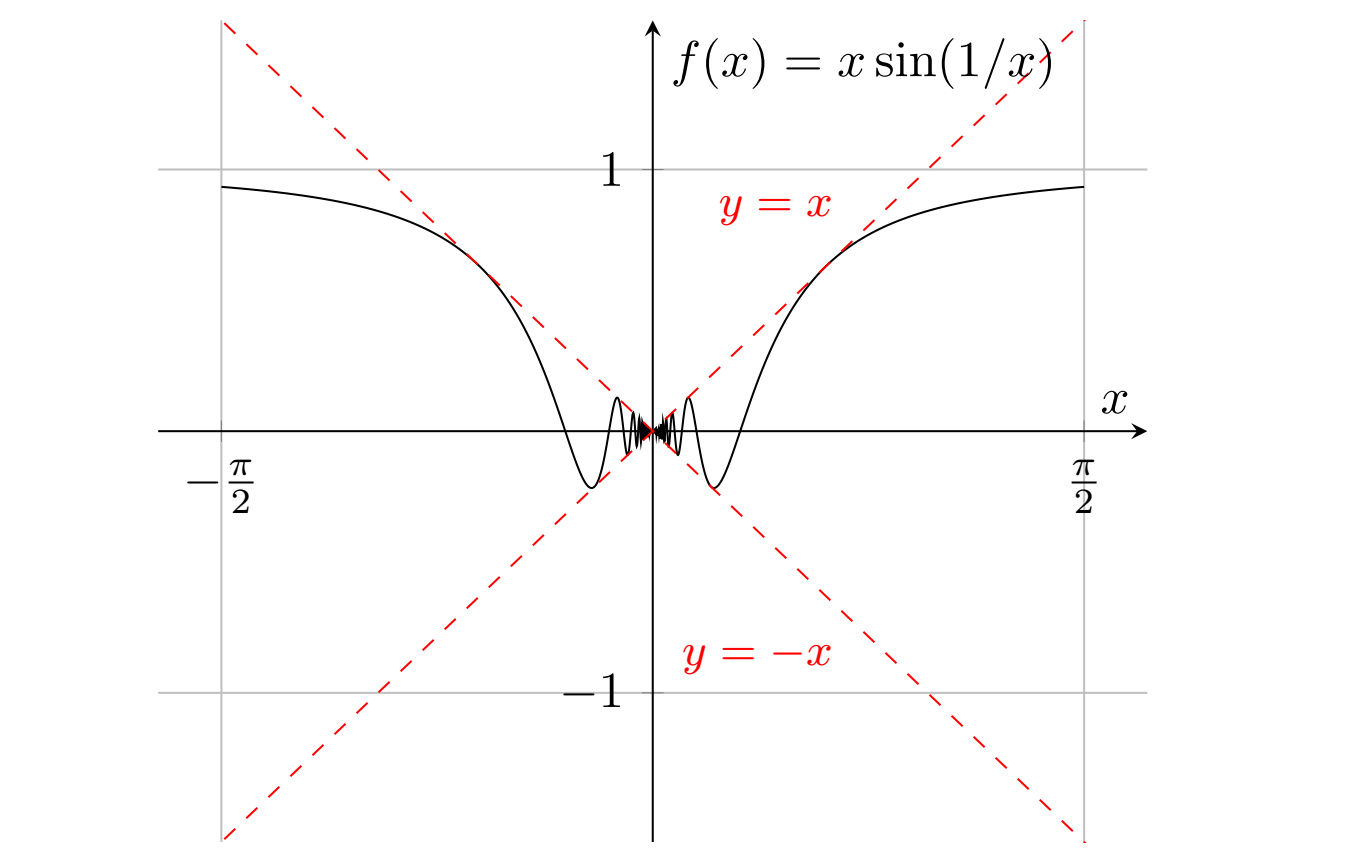
Let \( f: \mathbb{R} \to \mathbb{R} \) be defined as
Find the value of \( f(0) \) so that \( f(x) \) is continuous at \( x = 0 \).
Solution: To ensure continuity at \( x = 0 \), the function must satisfy
Since \( f(x) = x \sin(1/x) \) for \( x \neq 0 \), consider what happens as \( x \to 0 \). The function \( \sin(1/x) \) oscillates infinitely between \( -1 \) and \( 1 \), but its amplitude is scaled by \( x \), which approaches zero. This suggests that \( x \sin(1/x) \) also approaches zero, despite the oscillations. Thus, an intuitive choice is to define \( f(0) = 0 \), ensuring that \( f(0) \) matches the limiting behavior of \( f(x) \).
A more formal argument follows from the Sandwich Theorem. Since
multiplying by \( x \) gives
Taking limits on both sides as \( x \to 0 \),
By the Sandwich Theorem, it follows that
For continuity, \( f(0) \) must equal this limit, so defining
ensures that \( f(x) \) is continuous at \( x = 0 \).
Example
Check the continuity of \( f(x) = \lfloor x \rfloor - \lfloor 3x \rfloor \) at \( x = 1 \).
Solution: Continuity at \( x = 1 \) requires
First, evaluate \( f(1) \). Since the greatest integer function satisfies \( \lfloor a \rfloor \) as the largest integer less than or equal to \( a \),
To determine \( \lim\limits_{x \to 1} f(x) \), compute the right-hand limit and left-hand limit separately.
For the right-hand limit,
For \( x \to 1^+ \), \( 1<x<2 \) but arbitrarily close to 1, so
For \( \lfloor 3x \rfloor \), since \( x>1 \) and approaching 1, implies \( 2< 3x < 3 \), it follows that
Thus,
For the left-hand limit,
For \( x \to 1^- \), \( 0 < x < 1 \), so
For \( \lfloor 3x \rfloor \), since \( x \to 1^- \) implies \( 3x \to 3^- \), it follows that
Thus,
Since both one-sided limits are equal and agree with \( f(1) \),
By the definition of continuity, \( f(x) \) is continuous at \( x = 1 \).
Discontinuities
A function is discontinuous at \( x = a \) if it fails to satisfy the condition
Discontinuities can be classified into various types based on how the function misbehaves at the point.
Isolated Point Discontinuity
One fundamental type is when the limit \( \lim\limits_{x \to a} f(x) \) exists but does not match \( f(a) \). This is known as an isolated point discontinuity.
An example of such a discontinuity occurs in the function
To check continuity at \( x = 0 \), compute the limit:
Since \( f(0) = 0 \) but the limit approaches \( 1 \), the function is discontinuous at \( x = 0 \) due to an isolated point discontinuity. If \( f(0) \) were redefined as \( 1 \), the discontinuity would be removed, making \( f(x) \) continuous at \( x = 0 \).
Missing Point Discontinuity
A missing point discontinuity occurs when a function is not defined at some internal point in its domain, even though the limit of the function exists at that point. This creates a hole in the graph at \( x = a \), as the function approaches a well-defined value but does not actually attain it at that point. Such discontinuities can often be removed by appropriately defining the function at the missing point.
Consider the function
This function is not defined at \( x = 1 \) because the denominator becomes zero, making the expression meaningless. However, simplifying the function algebraically,
Taking the limit as \( x \to 1 \),
The limit exists and is finite, meaning the function behaves well near \( x = 1 \), but a discontinuity arises solely because \( f(x) \) is undefined at \( x = 1 \). This creates a hole in the graph at \( x = 1 \), where the function should take the value 2, but does not.
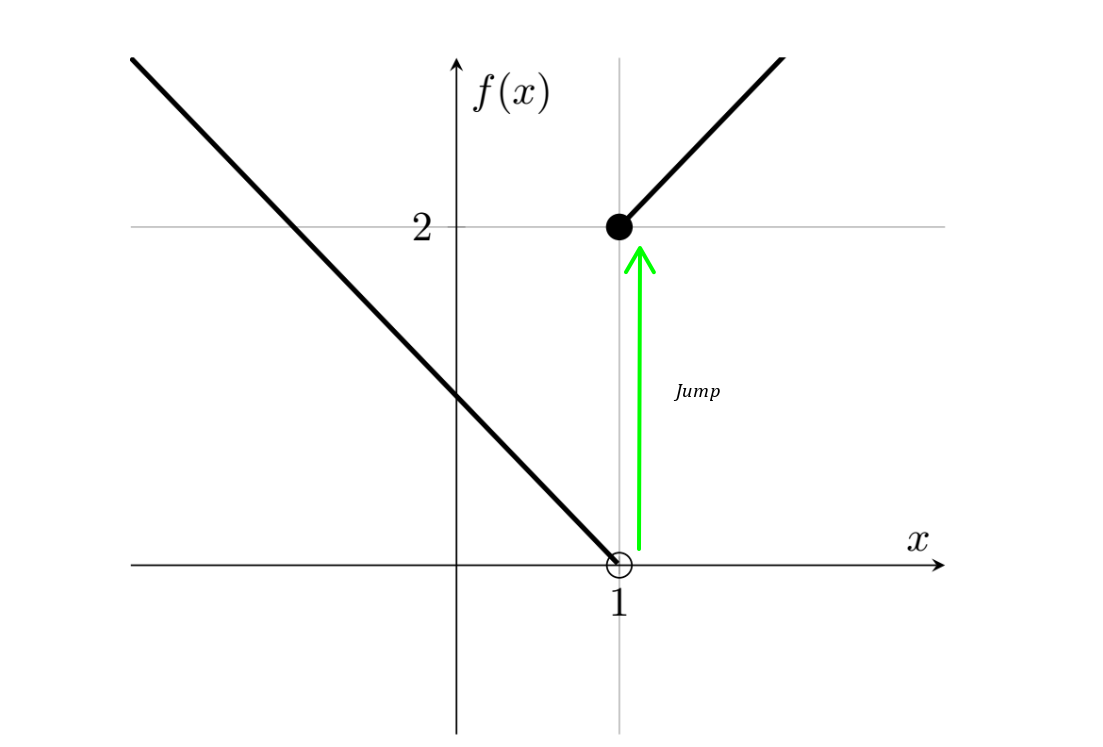
Jump Discontinuity
A jump discontinuity occurs at \( x = a \) when the left-hand limit and right-hand limit exist but are not equal, meaning the function has an abrupt change in value at \( x = a \).
Consider the function
To check continuity at \( x = 1 \), compute the left-hand and right-hand limits separately.
For \( x \to 1^- \), the function follows \( f(x) = 1 - x \), so
For \( x \to 1^+ \), the function follows \( f(x) = x + 1 \), so
Since
the two-sided limit \( \lim\limits_{x \to 1} f(x) \) does not exist, indicating a jump discontinuity at \( x = 1 \). The function abruptly jumps from \( 0 \) to \( 2 \), creating a visible gap in the graph.
Infinite Point Discontinuity
An infinite point discontinuity occurs at an internal point \( x = a \) when the function becomes unbounded as \( x \to a \). This means that at least one of the one-sided limits approaches \( \infty \) or \( -\infty \), causing the function to diverge instead of settling at a finite value. Unlike missing point or jump discontinuities, which involve gaps or abrupt changes in function values, an infinite discontinuity represents a singularity where the function blows up.
A standard example is the function
This function is not defined at \( x = 0 \) because the denominator becomes zero. To examine its behavior as \( x \to 0 \), consider the left-hand and right-hand limits separately.
For \( x \to 0^- \), where \( x \) is slightly negative,
For \( x \to 0^+ \), where \( x \) is slightly positive,
Since these one-sided limits do not agree and both tend to infinity (but in opposite directions), the function exhibits an infinite point discontinuity at \( x = 0 \). The graph of \( f(x) \) has a vertical asymptote at \( x = 0 \), meaning the function grows arbitrarily large or small as it approaches the discontinuity.
Oscillatory Point Discontinuity
An oscillatory point discontinuity occurs at \( x = a \) when the function oscillates infinitely as \( x \to a \), preventing the existence of a well-defined limit. Unlike other types of discontinuities where the function either jumps, remains undefined, or diverges to infinity, here the function fluctuates between different values infinitely often as it approaches the discontinuous point. As a result, neither a finite limit nor an infinite limit exists at \( x = a \).
A classic example of an oscillatory point discontinuity is the function
This function is not defined at \( x = 0 \), since \( 1/x \) is undefined at \( x = 0 \). To analyze its behavior, consider what happens as \( x \to 0 \) from both sides.
As \( x \to 0^+ \) (i.e., \( x \) is small and positive), the expression \( 1/x \) grows arbitrarily large, causing \( \sin(1/x) \) to oscillate infinitely between \( -1 \) and \( 1 \) with increasingly rapid frequency. Similarly, for \( x \to 0^- \), the same oscillatory behavior occurs. The key observation is that the function does not settle to a single value or approach a finite limit. Instead, it keeps fluctuating without stabilizing, meaning that
Since the function fails to have a well-defined limit at \( x = 0 \), it is discontinuous at that point. The discontinuity is not due to a missing function value, a jump, or infinite divergence, but rather due to wild oscillations that persist indefinitely as \( x \to 0 \).
Removable and Irremovable Discontinuities
Discontinuities can also be classified based on whether they can be eliminated by redefining the function at \( x = a \).
A removable discontinuity occurs when the limit \( \lim\limits_{x \to a} f(x) \) exists and is finite, but either \( f(a) \) is not defined or \( f(a) \) is not equal to this limit. In such cases, continuity can be restored by redefining \( f(a) \) to match the limit. Isolated point discontinuities and missing point discontinuities are examples of removable discontinuities because the function behaves well near \( x = a \) but has a gap or hole at that point.
An irremovable (fundamental) discontinuity occurs when the function has a break that cannot be fixed by redefining \( f(a) \). This happens in three main cases:
- A jump discontinuity, where the left-hand and right-hand limits exist but are not equal, causing an abrupt change in function value.
- An infinite discontinuity, where the function goes to infinity near \( x = a \), meaning at least one of the one-sided limits is \( \infty \) or \( -\infty \).
- An oscillatory discontinuity, where the function fluctuates wildly near \( x = a \) without approaching a single value.
In these cases, there is no possible value of \( f(a) \) that can make the function continuous at \( x = a \). The discontinuity is an essential feature of the function and cannot be removed by simply filling in a missing value.
One-sided Continuity
A function \( f(x) \) is said to be continuous from the left, or simply left continuous at \( x = a \) if
Similarly, \( f(x) \) is continuous from the right, or simply right continuous at \( x = a \) if
These conditions mean that as \( x \) approaches \( a \) from either the left or right, the function smoothly reaches \( f(a) \) without any jumps, gaps, or undefined behavior. If both one-sided limits exist and equal \( f(a) \), then the function is fully continuous at \( x = a \).
However, if a function is continuous from only one side but not the other, it is said to have one-sided continuity at that point. This often happens when the function is only defined for \( x \geq a \) or \( x \leq a \), as in piecewise functions.
For example, consider
For \( x \to 2^- \), the function follows \( f(x) = x^2 \), so
For \( x \to 2^+ \), the function follows \( f(x) = x + 1 \), so
Since \( \lim\limits_{x \to 2^-} f(x) = f(2) = 4 \), the function is left-continuous at \( x = 2 \). But because \( \lim\limits_{x \to 2^+} f(x) \neq f(2) \), the function is not right-continuous at \( x = 2 \), meaning it is not fully continuous at that point.
Consider another example:
The greatest integer function, denoted by \( f(x) = \lfloor x \rfloor \), is discontinuous at all integer points. At every integer \( n \), the function exhibits a jump discontinuity because the left-hand limit and right-hand limit at \( x = n \) are not equal. However, the function remains right-continuous at all integers.
For any integer \( n \), the function satisfies
To analyze its continuity at integer points, consider the one-sided limits.
For \( x \to n^+ \) (i.e., \( x \) approaches \( n \) from the right), since \( x \geq n \), the greatest integer function gives
For \( x \to n^- \) (i.e., \( x \) approaches \( n \) from the left), since \( x < n \), the greatest integer function gives
Since
the function has a jump discontinuity at every integer \( n \). However, since
the function is right-continuous at every integer. This means that while the function has abrupt jumps at integer points, it does not break from the right; it smoothly connects to \( f(n) \) when approached from the right.