Wavy Curve Method

Introduction

Consider the inequality \( (x-1)(x-2)(x-3) < 0 \). To determine the values of \( x \) that make this inequality true, one might initially think to test every possible combination of signs for the three factors. This results in considering four distinct cases, as the product of three numbers can be negative only if an odd number of the factors are negative:

1. \( x-1 \) is positive, \( x-2 \) is positive, and \( x-3 \) is negative.
2. \( x-1 \) is positive, \( x-2 \) is negative, and \( x-3 \) is positive.
3. \( x-1 \) is negative, \( x-2 \) is positive, and \( x-3 \) is positive.
4. \( x-1 \) is negative, \( x-2 \) is negative, and \( x-3 \) is negative.

Evaluating each case separately would certainly yield the correct intervals for \( x \), but it would take quite a bit of time and effort. Imagine doing this for inequalities with even more factors—it would get unwieldy very quickly! That's where the sign scheme, or the wavy curve method, steps in. It's a powerful technique that leverages the properties of continuous functions and the behavior of their zeros to quickly determine where a product of factors is gretaer than or less than zero. This method transforms a potentially cumbersome process into a swift and satisfying solution, capturing the true spirit of mathematical problem-solving. It's about being clever, not just correct.

Sign Scheme

To understand let us solve the following problem:

Solve for real values of \( x \) such that \( (x-1)(x-2)(x-3) < 0 \).

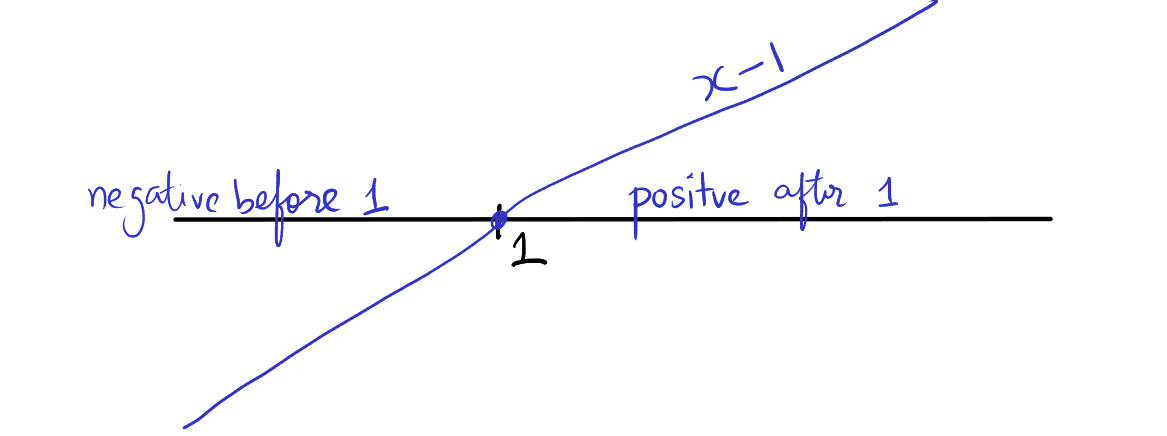
To solve inequalities involving multiple factors such as \( x-1 \), \( x-2 \), and \( x-3 \), we can analyze each factor separately. Take \( x-1 \) for example. This factor equals zero when \( x = 1 \). If we substitute any value greater than 1 into \( x-1 \), the result is a positive number. Conversely, if we put in any value less than 1, the result is negative.

We can visualize this on a number line. At the point where \( x = 1 \), which is the zero of this factor, there is a change in sign. To the right of 1, the expression \( x-1 \) is positive, while to the left of 1, it is negative. This can be illustrated with a line that crosses the horizontal axis at \( x = 1 \), showing a change from negative to positive as it crosses this point. The line slopes upwards as it moves to the right, indicating the values of \( x-1 \) are positive after \( x = 1 \) and negative before it. This simple visual helps determine the sign of \( x-1 \) for any real number \( x \) and is a crucial step in solving the given inequality.

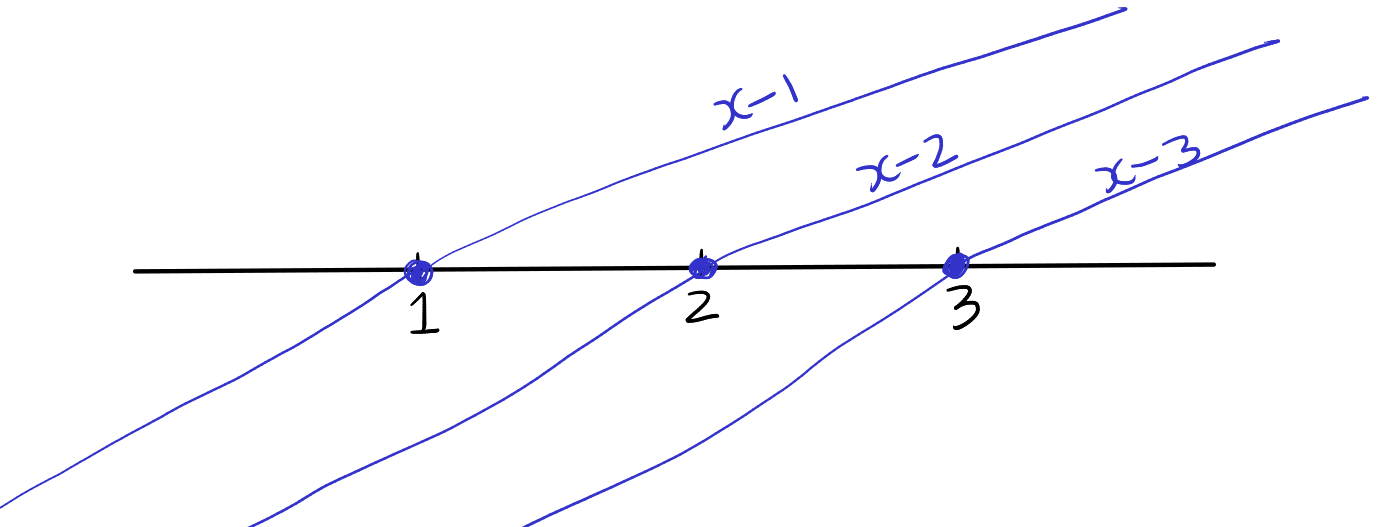
Similarly, for \(x-2\) and \(x-3\), we find that each factor is zero at \(x = 2\) and \(x = 3\), respectively. For values of \(x\) greater than 2, the expression \(x-2\) is positive, and for values less than 2, it's negative. The same logic applies to \(x-3\): it's positive for \(x\) values greater than 3 and negative for those less than 3. By marking these points and their corresponding sign changes on the number line, we can determine the sign of each factor across different intervals of \(x\).

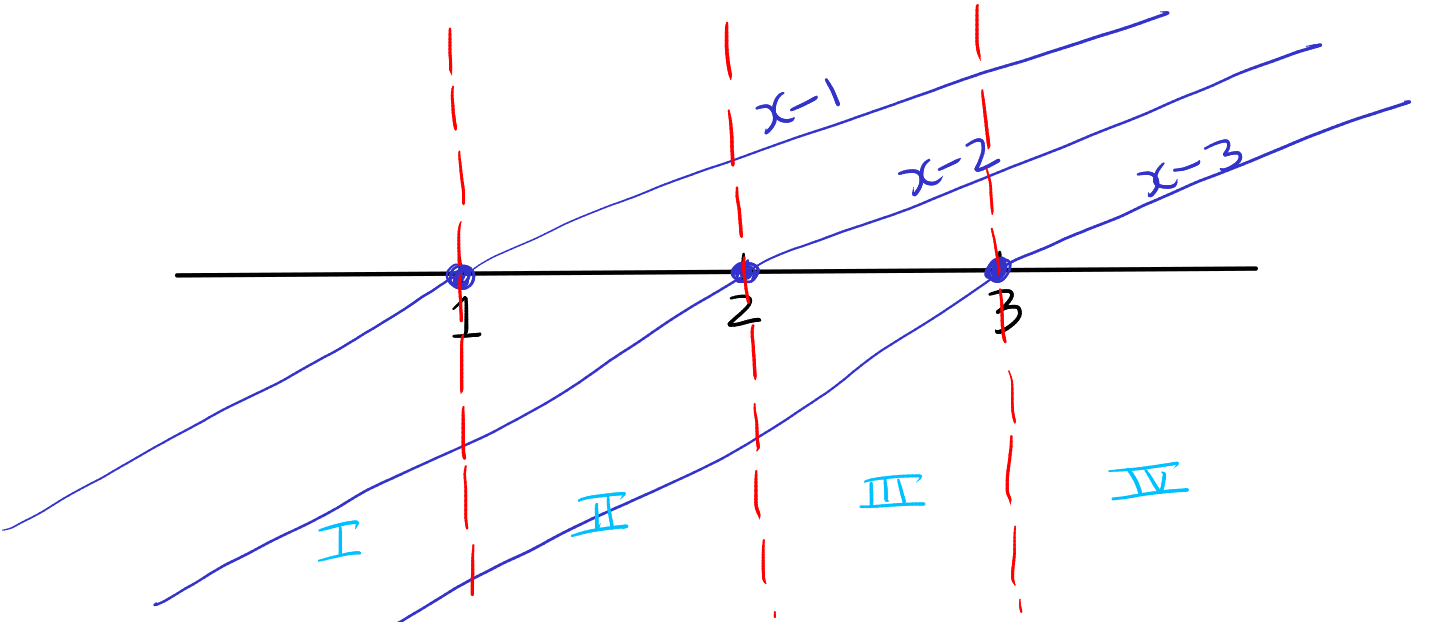
Then we divide the real line at the roots 1, 2, and 3 into four intervals. These roots are the points where the expressions \( x-1 \), \( x-2 \), and \( x-3 \) change their signs. The intervals created are as follows:

I. To the left of 1, where \( x < 1 \).

II. Between 1 and 2, where \( 1 < x < 2 \).

III. Between 2 and 3, where \( 2 < x < 3 \).

IV. To the right of 3, where \( x > 3 \).

In each of these intervals, the signs of the factors \( x-1 \), \( x-2 \), and \( x-3 \) will be consistent throughout the interval but will change as we cross each root. This division allows us to determine the sign of the entire expression \( (x-1)(x-2)(x-3) \) for any \( x \) within these intervals.

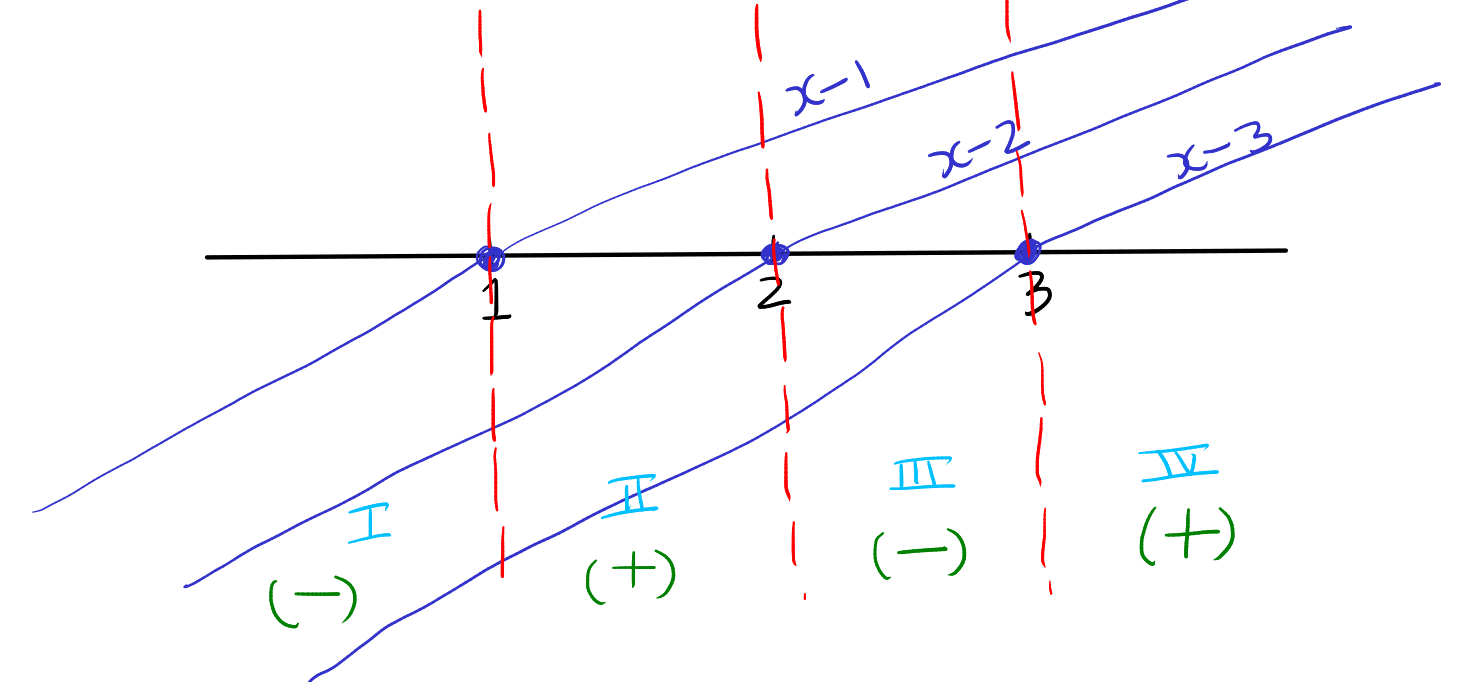
In each interval, we analyze the final sign of the expression \( (x-1)(x-2)(x-3) \) based on the number of negative factors within that interval:

I. For \( x < 1 \): All three factors, \( (x-1) \), \( (x-2) \), and \( (x-3) \), are negative because \( x \) is less than all three roots. The product of three negative numbers is negative, so the expression is negative in this interval.

II. For \( 1 < x < 2 \): The factor \( (x-1) \) is positive, but \( (x-2) \) and \( (x-3) \) are still negative. The product of one positive and two negative numbers is positive, making the expression positive in this interval.

III. For \( 2 < x < 3 \): The factors \( (x-1) \) and \( (x-2) \) are positive, but \( (x-3) \) is negative. The product of two positive numbers and one negative number is negative, so the expression is negative in this interval.

IV. For \( x > 3 \): All three factors, \( (x-1) \), \( (x-2) \), and \( (x-3) \), are positive as \( x \) is greater than all three roots. The product of three positive numbers is positive, therefore the expression is positive in this interval.

By looking at the sign changes across these intervals, we can determine the solution to the inequality \( (x-1)(x-2)(x-3) < 0 \) is the union of intervals where the expression is negative, which are intervals I and III.

The final answer in interval form for the solution to the inequality \( (x-1)(x-2)(x-3) < 0 \) is:

\( x \in (-\infty, 1) \cup (2, 3) \)

Example

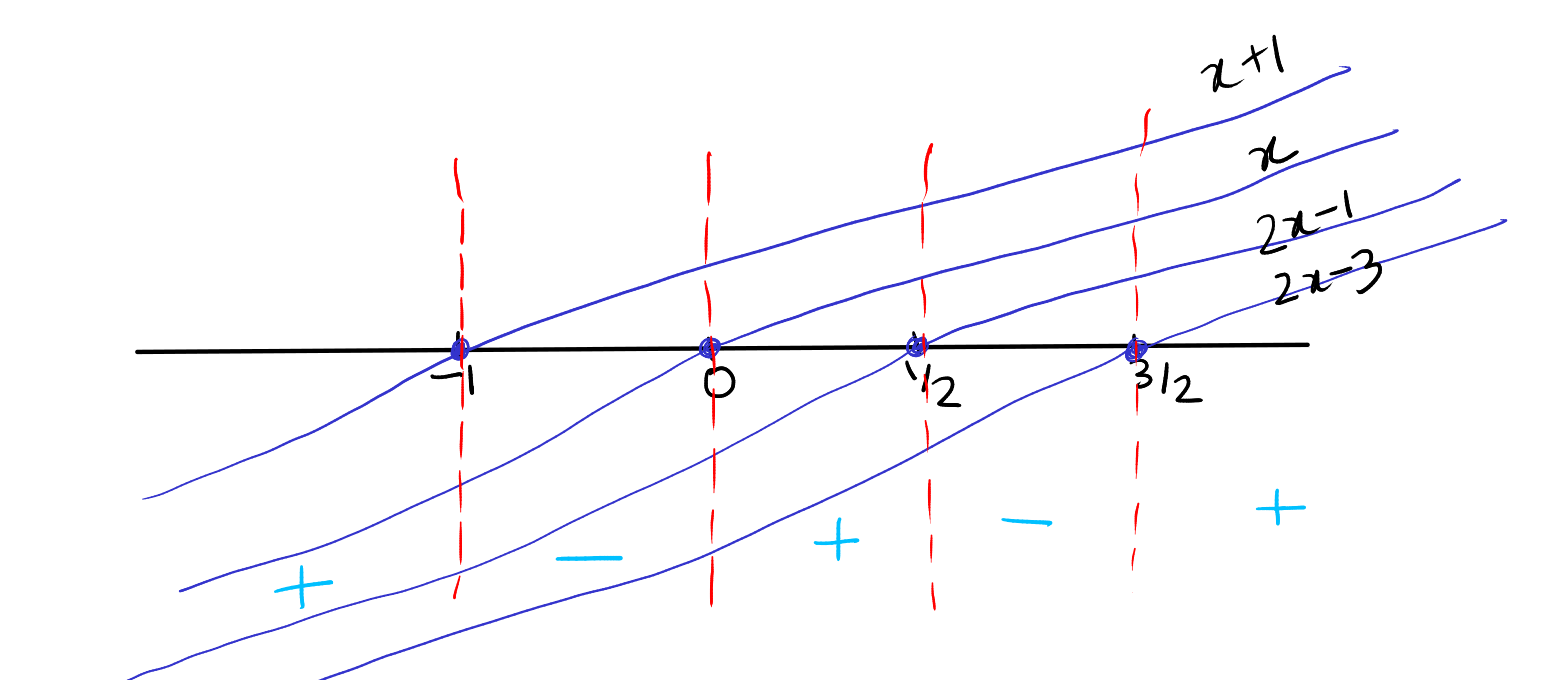
Solve the inequality for real values of \( x \) where the product \( x(x+1)(2x-1)(2x-3) \geq 0 \).

Solution:

To solve the inequality \( x(x+1)(2x-1)(2x-3) \geq 0 \), we consider the roots of each factor, which are \( x = 0 \), \( x = -1 \), \( x = \frac{1}{2} \), and \( x = \frac{3}{2} \).

Place these roots on a number line, which divides it into intervals:

• To the left of -1
• Between -1 and 0
• Between 0 and \( \frac{1}{2} \)
• Between \( \frac{1}{2} \) and \( \frac{3}{2} \)
• To the right of \( \frac{3}{2} \)

Now decide the sign of each factor by drawing lines.

Now we determine the sign of the product in each interval:

• To the left of -1: The product is positive because we have an even number (4) of negative factors.
• Between -1 and 0: The product is negative because there are 3 negative factors (an odd number).
• Between 0 and \( \frac{1}{2} \): The product is positive with 2 negative factors.
• Between \( \frac{1}{2} \) and \( \frac{3}{2} \): The product is negative with 1 negative factor.
• To the right of \( \frac{3}{2} \): The product is positive with 0 negative factors.

The inequality \( x(x+1)(2x-1)(2x-3) \geq 0 \) is satisfied in intervals where the product is non-negative. Therefore, the solution in interval notation is:

\[ x \in (-\infty, -1] \cup [0, \frac{1}{2}] \cup [\frac{3}{2}, \infty) \]

Closed brackets are used in interval notation to indicate that the endpoints are included in the solution set. This means that at the values \( x = -1 \), \( x = 0 \), and \( x = \frac{3}{2} \), the product \( x(x+1)(2x-1)(2x-3) \) is exactly zero, which satisfies the inequality \( \geq 0 \). Hence, these points are part of the solution and are represented with closed brackets [ ].

Example

Solve for real values of \(x\) which satisfies the inequation:

\[ \frac{(x+1)(x-2)}{x+3} \leq 0 \]

Solution:

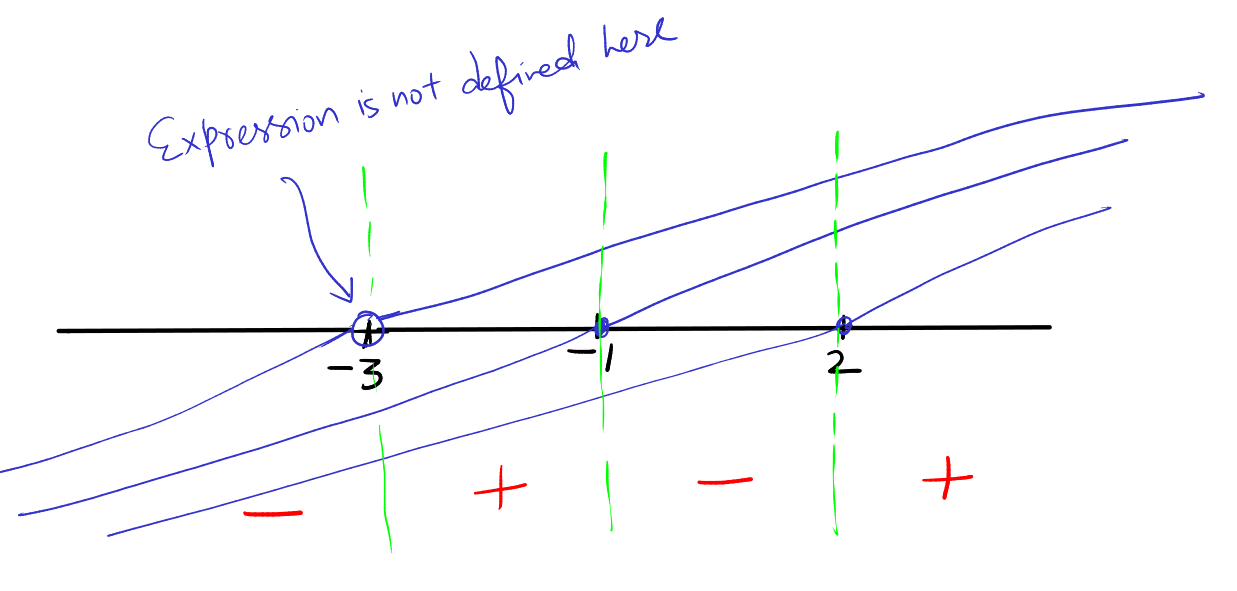
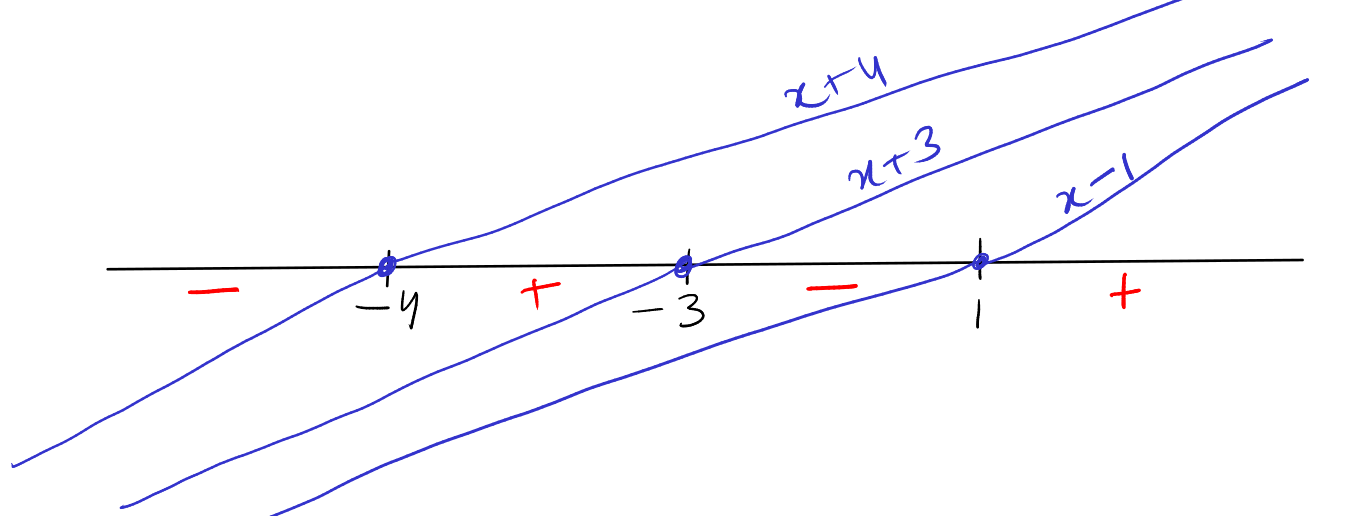
To solve the inequality \( \frac{x+1}{x+3} (x-2) \leq 0 \), we must consider the points where the expression changes sign, which are the roots of the numerator, \( x = -1 \) and \( x = 2 \), and the root of the denominator, \( x = -3 \).

Analyze the sign of each factor about its root.

Now let's determine the sign of the expression within each interval:

• For \( x < -3 \): Both \( x+1 \) and \( x-2 \) are negative, but the denominator \( x+3 \) is also negative, making the entire expression positive.
• Between \( -3 \) and \( -1 \): The \( x+1 \) is negative, \( x-2 \) is negative, and \( x+3 \) is positive, thus the expression is positive.
• Between \( -1 \) and \( 2 \): The \( x+1 \) is positive, \( x-2 \) is negative, and \( x+3 \) is positive, making the expression negative.
• For \( x > 2 \): Both \( x+1 \) and \( x-2 \) are positive, and since the denominator \( x+3 \) is also positive, the entire expression is positive.

We are looking for intervals where the expression is less than or equal to zero. Based on the sign analysis:

• \( x = -1 \) is included because it makes the expression equal to zero.
• \( x = 2 \) is included for the same reason.
• \( x = -3 \) is excluded because the expression is undefined.

The solution in interval notation is:

\[ x \in (-\infty, -3) \cup [-1, 2] \]

Example

Solve the following inequalities:

a. \( (3x-5)(4x-3)(x+1) < 0 \)

b. \( (x+1)(x-3)(3+x) \geq 0 \)

c. \( (x^2+1)(x+3)(x-1)(x+4) \leq 0 \)

Solution:

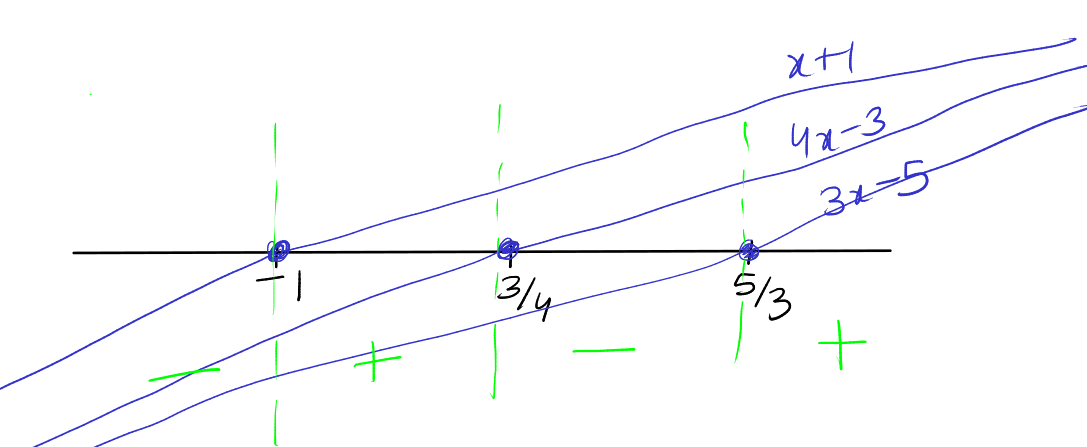
a. To solve the inequality \( (3x-5)(4x-3)(x+1) < 0 \), we'll analyze the sign of the product by determining the roots of each factor:

1. \(3x - 5 = 0\) gives \(x = \frac{5}{3}\).
2. \(4x - 3 = 0\) gives \(x = \frac{3}{4}\).
3. \(x + 1 = 0\) gives \(x = -1\).

These roots split the number line into four intervals. We then decide the sign of each factor in the intervals:

• For \(x < -1\): All three factors are negative.
• Between \(-1\) and \(\frac{3}{4}\): The factor \(x+1\) is positive, but the other two factors are negative.
• Between \(\frac{3}{4}\) and \(\frac{5}{3}\): All three factors are positive.
• For \(x > \frac{5}{3}\): The factors \(3x-5\) and \(x+1\) are positive, but \(4x-3\) is negative.

Since we are looking for the intervals where the product is negative, the solution to the inequality will be the union of intervals where we have an odd number of negative signs:

\[ x \in (-\infty, -1) \cup \left(\frac{3}{4}, \frac{5}{3}\right) \]

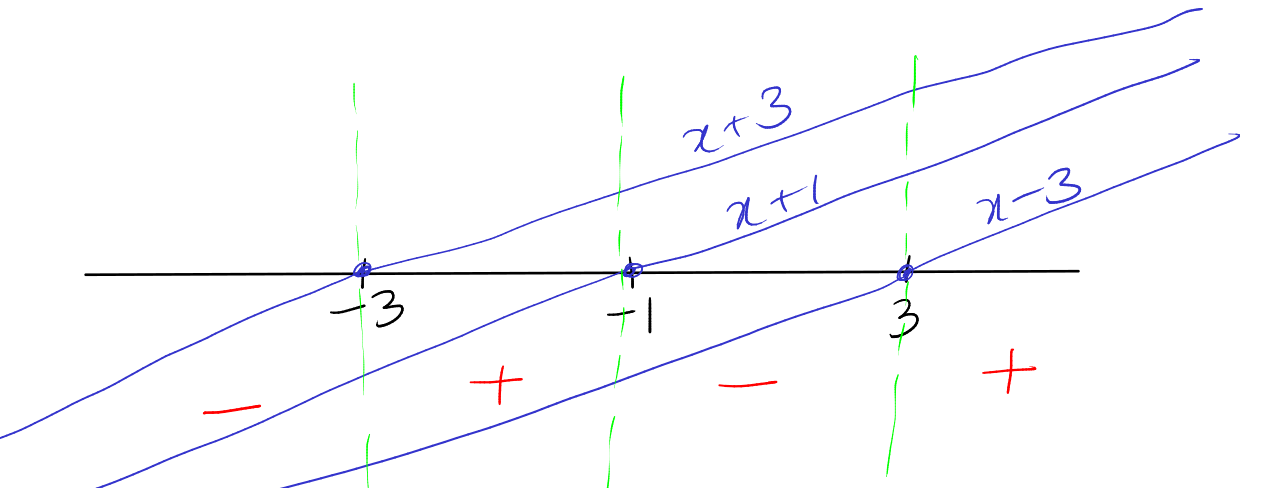
b. To solve the inequality \( (x+1)(x-3)(3+x) \geq 0 \), let's determine the zeros of each factor:

1. \(x + 1 = 0\) gives \(x = -1\).
2. \(x - 3 = 0\) gives \(x = 3\).
3. \(3 + x = 0\) is the same as \(x + 3 = 0\), giving \(x = -3\).

These zeros divide the real line into four intervals. We'll analyze the sign of the product in each interval:

• For \(x < -3\): All three factors are negative. The product is negative.
• Between \(-3\) and \(-1\): Two factors are negative, one is positive. The product is positive.
• Between \(-1\) and \(3\): Two factors are positive, one is negative. The product is negative.
• For \(x > 3\): All factors are positive. The product is positive.

Since we are looking for the intervals where the product of the factors is non-negative, the solution to the inequality will include the intervals where the product is positive and the zeros where the product equals zero:

\[ x \in [-3, -1] \cup [3, \infty) \]

c. The factor \( x^2+1 \) is always positive since the sum of a square and a positive number cannot be zero or negative for any real number \( x \).

Now let's consider the zeros of the other factors:

1. \( x + 3 = 0 \) gives \( x = -3 \).
2. \( x - 1 = 0 \) gives \( x = 1 \).
3. \( x + 4 = 0 \) gives \( x = -4 \).

These zeros divide the real line into intervals. Since \( x^2+1 \) is always positive, it does not affect the sign of the inequality. We then analyze the sign of the product for the remaining factors within each interval:

• For \( x < -4 \): \( x+3 \) and \( x+4 \) are negative, \( x-1 \) is negative. The product is positive.
• Between \( -4 \) and \( -3 \): \( x+3 \) is negative, \( x+4 \) is positive, \( x-1 \) is negative. The product is negative.
• Between \( -3 \) and \( 1 \): \( x+3 \) is positive, \( x+4 \) is positive, \( x-1 \) is negative. The product is negative.
• For \( x > 1 \): \( x+3 \) is positive, \( x+4 \) is positive, \( x-1 \) is positive. The product is positive.

We are looking for where the product is non-positive. Therefore, the solution to the inequality is where the expression is negative or zero:

\[ x \in (-\infty, -4] \cup [-3, 1] \]

Rules to draw wavy curve or sign scheme

Rule 1: Drawing the Wavy Curve from distinct Factors

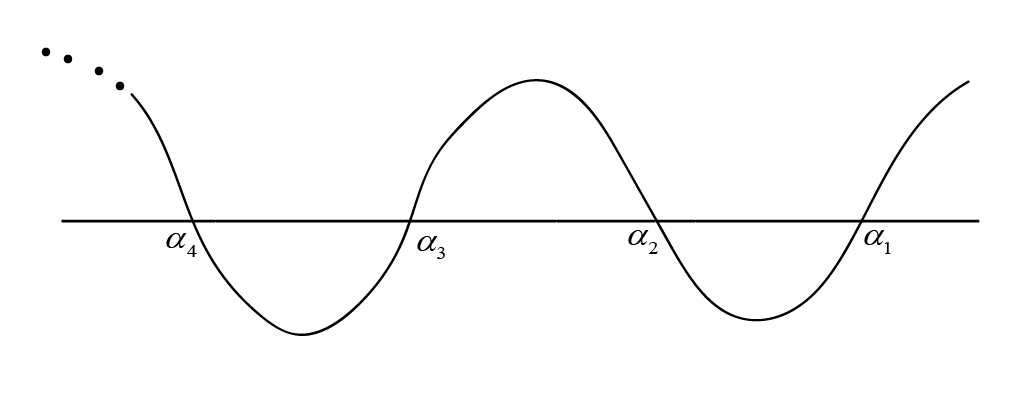
Consider a polynomial \( p(x) \) given in factored form as \( (x-\alpha_1)(x-\alpha_2)\ldots(x-\alpha_n) \), where \( \alpha_1, \alpha_2, \ldots, \alpha_n \) are all distinct real numbers.

1. Identify and Arrange Roots:

   • Plot these roots, \( \alpha_1, \alpha_2, \ldots, \alpha_n \), on the real line in ascending order.

2. Starting Point:

   • Begin from the rightmost root on the real line.

3. Draw the Curve:

   • Start drawing the curve from the rightmost side, initiating from above the real line.
   • As you approach each root \( \alpha_i \), the curve should pass through the real line at \( \alpha_i \).
   • After crossing \( \alpha_i \), alternate the direction of the curve:
   • If the curve approached \( \alpha_i \) from above, it should leave going below the real line.
     • Conversely, if it approached from below, it should leave going above the real line.

4. Wave Characteristics:

   • Between each pair of roots \( \alpha_i \) and \( \alpha_{i+1} \), ensure the curve has exactly one peak or trough, depending on the direction you've just switched from.
   • The number of changes in direction (from up to down or down to up) across the entire graph is determined by the number of roots \( n \).

Example

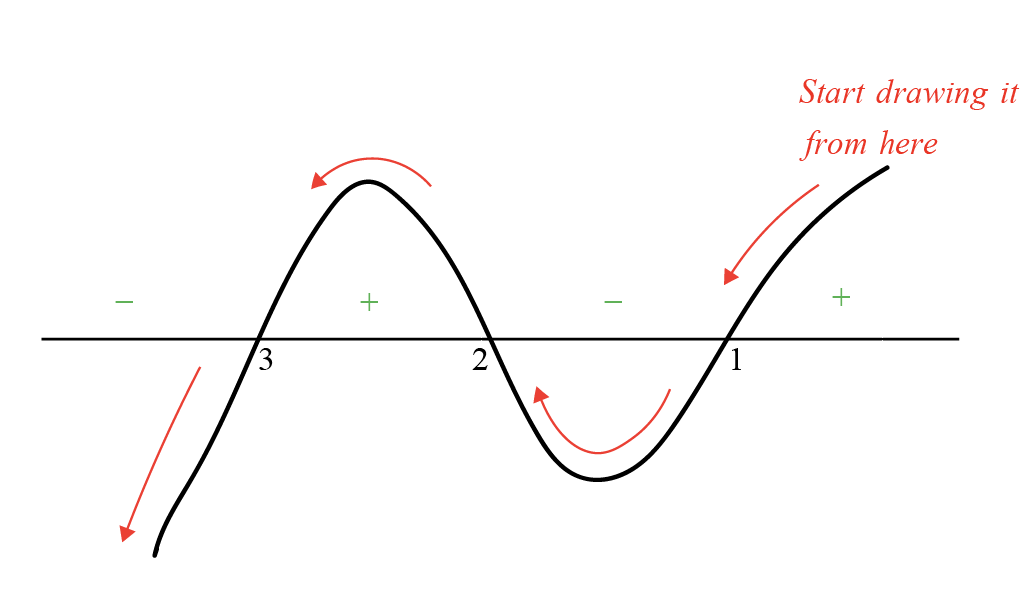
Draw the wavy curve of \( (x-1)(x-2)(x-3) \).

Solution:

Steps to Draw the Wavy Curve:

1. Identify and Plot Points:

   • Mark three points on the horizontal line (which represents different values of x): 1, 2, and 3. These are the important points where the curve will change direction.

2. Start Drawing the Curve:

   • Begin from the right side of your drawing area, which is beyond the point 3. Start high above the line.

3. Approach the First Point (x=3):

   • Draw the curve coming down to touch the horizontal line right at point 3.

4. Curve Between Point 3 and 2:

   • After touching point 3, draw the curve going below the line, making a dip, and then back up to touch the line again at point 2.

5. Curve Between Point 2 and 1:

   • Once you hit point 2, let the curve go above the line, create an arc going up, and then come back down to touch the line at point 1.

6. Finish the Curve:

   • After reaching point 1, draw the curve dipping below the line and then curving back above it as you continue to the left.

This approach will show the curve intersecting the line at points 1, 2, and 3, each time changing direction from up to down or down to up, creating a wavy pattern across your drawing area.

Rule 2: Drawing Wavy Curves with Repeated Factors

1. Identify and Arrange Roots:

   • Write down the expression in its expanded form, identifying all roots, including repeated ones. For example, if the expression is \( (x-\alpha_1)^{r_1}(x-\alpha_2)^{r_2}\ldots \), identify \( \alpha_1, \alpha_2, \ldots \), and note the powers \( r_1, r_2, \ldots \).
   • Arrange these roots on the real line in ascending order of their values.

2. Starting Point:

   • Start drawing from the rightmost root on the real line, beginning from above the real line.

3. Drawing the Curve:

   • As you approach each root \( \alpha_i \), observe the corresponding power \(r_i\):
     • Odd Power \(r_i\): The curve is allowed to change sign, meaning it can cross the real line at the root \( \alpha_i \). This crossing reflects a sign change in the behavior of the curve.
     • Even Power \(r_i\): The curve touches the real line at the root \( \alpha_i \) but does not cross it. This indicates the curve reaches zero at the root but remains on the same side of the real line, bouncing back in the direction it came from.

4. Wave Characteristics:

   • For each segment between the roots:
     • Ensure that if the next root has an odd power, prepare to cross the line.
     • If the next root has an even power, ensure the curve approaches the line, touches it, and then returns without crossing.

This rule helps in visualizing and drawing curves for expressions where factors might be repeated, impacting how the curve behaves at each root based on the parity of the powers associated with those factors.

Example

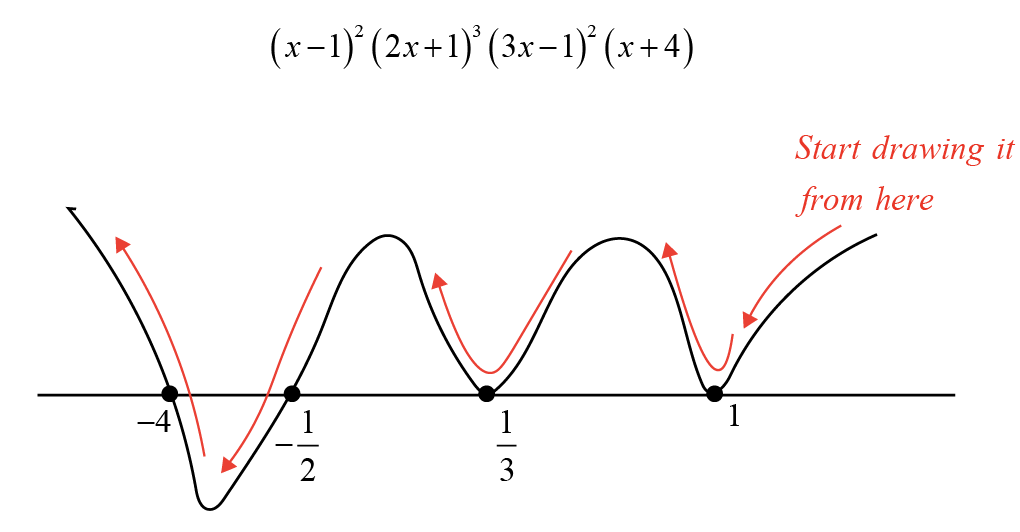
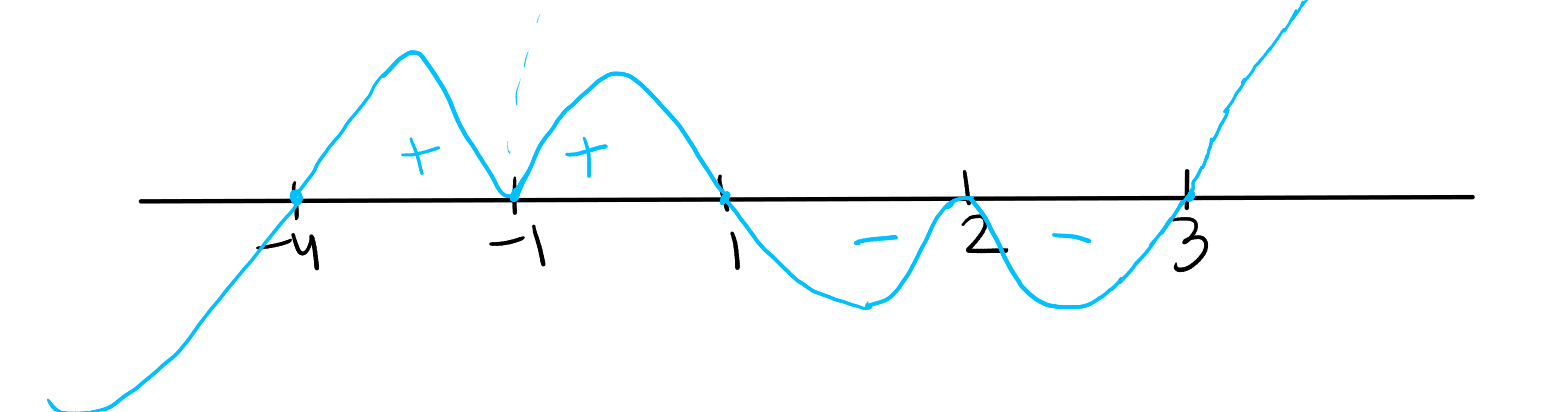
Sketch the wavy curve of the expression \( (x-1)^2(2x+1)^3(3x-1)^2(x+4) \).

1. Plot the Roots:

   • Mark the roots of the expression where each factor is zero: \( x = 1, -\frac{1}{2}, \frac{1}{3}, \) and \( -4 \).

2. Determine the Multiplicity of Each Root:

   • Observe the powers of each factor to determine how the curve behaves at each root.
   • Roots at \( x = 1 \) and \( x = \frac{1}{3} \) have even multiplicities (squared terms), so the curve will touch thereal line at these points but not cross it.
   • The root at \( x = -\frac{1}{2} \) has an odd multiplicity (cubed term), so the curve will cross the real line at this point.
   • The root at \( x = -4 \) is a simple root (to the first power), so the curve will also cross the real line here.

3. Draw the Curve:

   • Start from the rightmost point, which is to the right of the root \( x = 1 \), and start above the real line because of the positive leading coefficient.
   • The curve touches and bounces off the real line at \( x = 1 \) since it's an even multiplicity.
   • Between \( x = 1 \) and \( x = \frac{1}{3} \), the curve makes a complete wave, staying above the real line.
   • Again, at \( x = \frac{1}{3} \), the curve touches and bounces off since it’s an even multiplicity.
   • Between \( x = \frac{1}{3} \) and \( x = -\frac{1}{2} \), the curve makes another complete wave, crossing the real line at \( x = -\frac{1}{2} \) where the multiplicity is odd.
   • To the left of \( x = -\frac{1}{2} \), make another arc to touch and bounce off the real line at \( x = -4 \), and continue to the left end of the graph.

Example

Draw the wavy curve of

\[ (x-1)^3(x-2)^2(x+1)^2(x-3)(x+4)^3 \]

1. Mark the Points on the Real Line:

   • Place marks at \( x = 3 \), \( x = 2 \), \( x = 1 \), \( x = -1 \), and \( x = -4 \).

2. Decide the Curve's Interaction at Each Point:

   • The curve will cross the real line at \( x = 3 \) and \( x = -4 \) because these are to the power of 1 and 3, respectively (both odd).
   • At \( x = 2 \) and \( x = -1 \), the curve will touch the real line and turn back since these are to the power of 2 (even).
   • At \( x = 1 \), the curve will cross the real line because it's to the power of 3 (odd).

3. Draw the Wavy Curve:

   • Start to the right of \( x = 3 \), above the real line, and cross at \( x = 3 \).
   • Between \( x = 3 \) and \( x = 2 \), draw the curve going down, touch the real line at \( x = 2 \) without crossing, and then move back up.
   • Continue with a wave between \( x = 2 \) and \( x = 1 \), crossing the real line at \( x = 1 \).
   • From \( x = 1 \) to \( x = -1 \), draw the curve up and then back down, touching the real line at \( x = -1 \) without crossing, and then up again.
   • Between \( x = -1 \) and \( x = -4 \), the curve goes down, crosses the real line at \( x = -4 \), and continues to move down to the left.

Understood, let's go through the process without discussing divergence and by plotting all points in ascending order on the same real line:

General Expression

For an expression of the form:

\[ \frac{(x-\alpha_1)^{r1}(x-\alpha_2)^{r2}(x-\alpha_3)^{r3}\ldots}{(x-\beta_1)^{l1}(x-\beta_2)^{l2}(x-\beta_3)^{l3}\ldots} \]

Step 1: Plot Points on the Real Line

• Roots and Undefined Points: Place both \( \alpha \)'s and \( \beta \)'s on the same real line, in ascending order of their values. Use solid circles to represent \( \alpha \)'s where the curve will intersect the line, and hollow circles for \( \beta \)'s where the expression is not defined.

Step 2: Draw the Wavy Curve for Numerator Roots

• Interaction at \( \alpha \)'s: When you reach an \( \alpha_i \), allow the curve to interact with the real line based on the exponent \( r_i \):
  • If \( r_i \) is odd, the curve crosses the real line at \( \alpha_i \).
  • If \( r_i \) is even, the curve touches the real line at \( \alpha_i \) and then turns back.

Step 3: Indicate the Behavior at Denominator Points

• Approach \( \beta \)'s: When you come to a \( \beta_i \), treat the curve similarly depending on the exponent \( l_i \):

  • If \( l_i \) is odd, the curve will cross the real line at \( \beta_i \) but do not forget that the expression is undefined at \(\beta_i\).
  • If \( l_i \) is even, the curve will touch the real line at the hollow circle of \( \beta_i \) and turn back.

Step 4: Complete the Wavy Curve - Connecting Sections: Join the sections of the curve smoothly between the points, creating waves that correspond to the interactions at the solid and hollow circles, thus completing the wavy curve for the entire expression.

Example

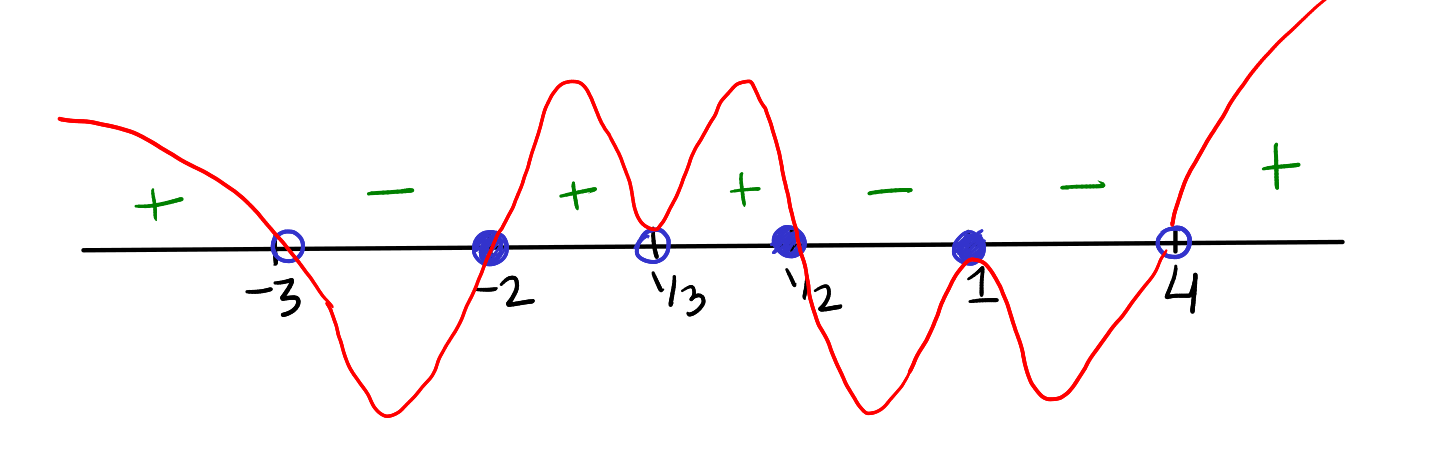
Given the expression:

\[ \frac{(x-1)^2(x+2)^2(2x-1)}{(3x-1)^2(x+3)(x-4)} \]

Draw the wavy curve and then find values of \(x\) for which this expression is greater then equalto zero.

Solution: To sketch the wavy curve for the given expression, we follow these steps:

1. Identify the Points of Interest:

   • The roots from the numerator are \( x = 1 \) (twice, due to the square) and \( x = -2 \) (twice, due to the square), and \( x = \frac{1}{2} \) (simple root).
   • The points from the denominator where the expression is undefined are \( x = \frac{1}{3} \) (twice, due to the square), \( x = -3 \) (simple root), and \( x = 4 \) (simple root).

2. Plot the Points on the Real Line:

   • Plot the all roots and undefined points on the real line in correct order
   • Place solid circles at \( x = 1 \), \( x = \frac{1}{2} \) and \( x = -2 \) to indicate that they are the roots of the expression.
   • Place hollow circles at \( x = -3 \), \( x = 4 \) and \( x = \frac{1}{3} \) to indicate the expression is not defined here.

3. Draw the Wavy Curve:

   • Begin above the real line to the right of \( x = 4 \) and move downwards.
   • The curve crosses the real line at \( x = 4 \) since it's a simple root in the denominator.
   • Between \( x = 4 \) and \( x = 1 \), the curve makes a wave that touches the real line at \( x = 1 \) without crossing and goes back up due to the squared factor in the numerator.
   • Between \( x = 1 \) and \( x = \frac{1}{2} \), the curve goes down, crosses the real line at \( x = \frac{1}{2} \), and continues to \( x = \frac{1}{3} \).
   • At \( x = \frac{1}{3} \), the curve comes close to the real line, indicating the expression is not defined, and goes back up.
   • Continue the curve to \( x = -2 \), where it touches the real line and turns back up due to the squared factor in the numerator.
   • The curve then proceeds to \( x = -3 \), where it sharply turns away from the real line without touching, again showing the expression is undefined at this point.
   • Finally, the curve extends to the left end, staying above the real line.

4. Final Touches:

   • Review the curve to ensure that at each solid circle, the expression either touches and turns back (for squared factors) or crosses the real line (for simple roots).
   • At each hollow circle, the curve approaches and then moves away, respecting the points where the expression is not defined (denominator roots).

   

As we can see in the wavy curve the expression is greater than or equal to zero for \( x \) in the intervals:

\[ (-\infty, -3) \cup [-2, \frac{1}{3}) \cup (\frac{1}{3}, \frac{1}{2}] \cup (4, \infty) \cup \{1\} \]