Polar Form of a Complex Number

Definition

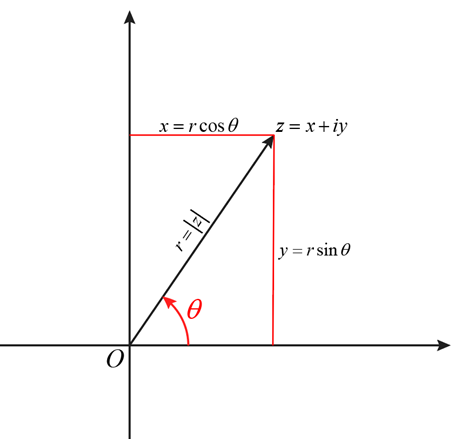
The polar form of a complex number is a way of expressing the number in terms of its magnitude and angle relative to the positive real axis. A complex number \( z \) can be written as \( z = x + iy \), where \( x \) and \( y \) are real numbers representing the real and imaginary parts of \( z \), respectively. In the complex plane, this number corresponds to the point \( P \) with Cartesian coordinates \( (x, y) \).

To convert the Cartesian coordinates to polar coordinates, we define \( r \) as the length of the vector \( OP \), which represents the magnitude of \( z \) and is given by \( r = |z| = \sqrt{x^2 + y^2} \). The angle \( \theta \), known as the argument of \( z \), is the angle between the positive real axis and the vector \( OP \).

The relationships between the Cartesian coordinates and the polar coordinates are given by:

\[ x = r \cos \theta \]

\[ y = r \sin \theta \]

So, the complex number \( z \) can also be expressed as:

\[ z = x + iy = r \cos \theta + ir \sin \theta \]

\[ z = r(\cos \theta + i \sin \theta) \]

Choosing Argument

Since argument of a complex number is not unique. If \(\theta\) is the argument, then \(2k\pi+\theta\) is also the argument for \(k\in\mathbb Z\). Therefore, the principal value of the argument, typically within the interval \((-π, π]\), is conventionally chosen for the polar form to maintain consistency and standardization across mathematical texts and computational tools.

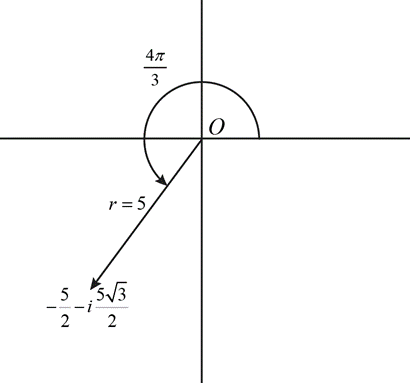
Consider a complex number \( z \), represented by point \( P \) on the complex plane. If the distance from the origin to \( P \) is 5, and the angle \( OP \) makes with the positive x-axis is \( \frac{4\pi}{3} \), then \( z \) is given by:

\[ z = 5\left(\cos \frac{4\pi}{3} + i\sin \frac{4\pi}{3}\right) \]

Using the cosine and sine values for the given angle, we can write \( z \) in Cartesian form:

\[ z = 5\left(-\frac{1}{2} - i\frac{\sqrt{3}}{2}\right) \]

\[ z = -\frac{5}{2} - i\frac{5\sqrt{3}}{2} \]

This is the Cartesian form of the complex number whose magnitude is 5 and whose argument (angle from the positive x-axis) is \( \frac{4\pi}{3} \).

Modulus of \(\cos(\theta) + i\sin(\theta)\)

\[\left| \cos(\theta) + i\sin(\theta) \right| = \sqrt{\cos^2(\theta) + \sin^2(\theta)} = \sqrt{1} = 1.\]

Some special considerations on polar form:

\( z = r(\cos\theta - i\sin\theta) \) is not in correct polar form, but we may convert it to correct form by using trigonometric identities.

\( z = r(\cos\theta - i\sin\theta) = r(\cos(-\theta) + i\sin(-\theta)) \) (Supposing \( r > 0 \))

Similarly,

Incorrect polar form	Correct polar form
\( r(-\cos\theta + i\sin\theta) \)	\( r(\cos(\pi - \theta) + i\sin(\pi - \theta)) \)
\( r(-\cos\theta - i\sin\theta) \)	\( r(\cos(\pi + \theta) + i\sin(\pi + \theta)) \)
\( r(\sin\theta + i\cos\theta) \)	\( r(\cos(\frac{\pi}{2} - \theta) + i\sin(\frac{\pi}{2} - \theta)) \)
\( r(\sin\theta - i\cos\theta) \)	\( r(\cos(\theta - \frac{\pi}{2}) + i\sin(\theta - \frac{\pi}{2})) \)
\( r(-\sin\theta + i\cos\theta) \)	\( r(\cos(\frac{\pi}{2} + \theta) + i\sin(\frac{\pi}{2} + \theta)) \)
\( r(-\sin\theta - i\cos\theta) \)	\( r(\cos(\frac{\pi}{2} - \theta) + i\sin(\frac{\pi}{2} - \theta)) \)

Example

Problem: Convert the complex number \( -1 - i \) to its polar form.

Solution:

Step 1: Find \( \alpha = \tan^{-1}\left(\frac{|y|}{|x|}\right) \). Given \( -1 - i \), we have \( x = -1 \) and \( y = -1 \). The magnitudes are \( |x| = 1 \) and \( |y| = 1 \). Thus,

\[ \alpha = \tan^{-1}\left(\frac{1}{1}\right) = \tan^{-1}(1) = \frac{\pi}{4}. \]

Step 2: Since \( -1 - i \) lies in the third quadrant, the argument \( \theta \) is \( -\pi + \alpha \). Hence,

\[ \theta = -\pi + \frac{\pi}{4} = -\frac{3\pi}{4}. \]

Step 3: We note that if \( \theta \) is the argument of a complex number, then \( 2k\pi + \theta \) is also an argument for \( k \in \mathbb{Z} \). We can choose any such argument for the polar form.

Step 4: Find \( r = |z| \). The modulus \( r \) is given by

\[ r = \sqrt{x^2 + y^2} = \sqrt{(-1)^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2}. \]

Thus, the polar form is

\[ r(\cos\theta + i\sin\theta) = \sqrt{2}\left(\cos\left(-\frac{3\pi}{4}\right) + i\sin\left(-\frac{3\pi}{4}\right)\right), \]

or using any argument \( 2k\pi + \theta \),

\[ \sqrt{2}\left(\cos\left(2k\pi - \frac{3\pi}{4}\right) + i\sin\left(2k\pi - \frac{3\pi}{4}\right)\right), \]

for \( k \in \mathbb{Z} \).