Radian Measure of Angles
What is wrong with degree system (also called sexagesimal system by the way)?
Degree system is very intuitive and is probably the best but it has a shortcoming. Why divide the circle into 360 equal parts? This number 360 which I explained before is just too arbitrary. We have a better system – the radian measure of angles.
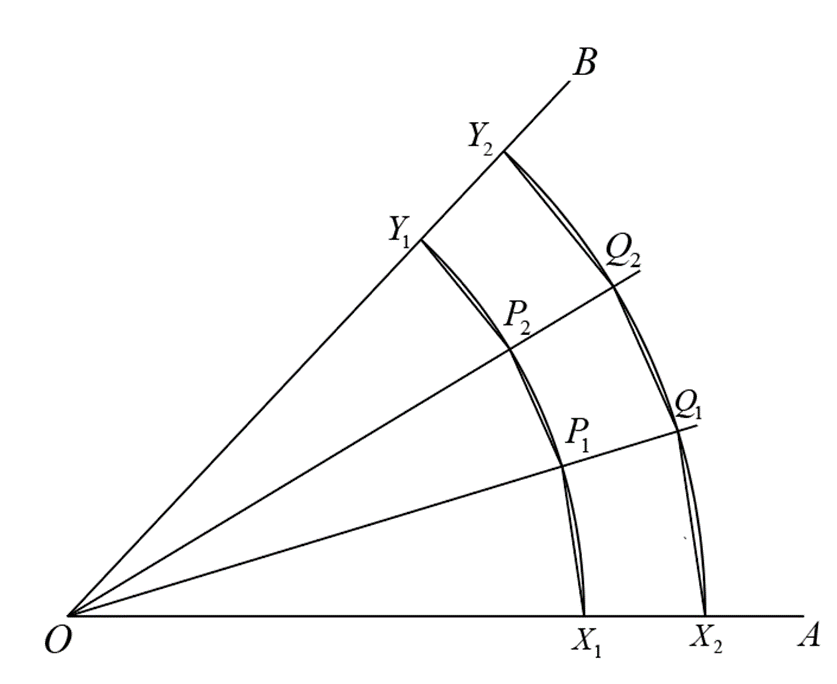
Let there be two diverging rays OA and OB emanating from point O. These rays contain some angle.
Draw an arc of any radius (say \( r_1 \)) intersecting the rays OA and OB at \( X_1 \) and \( Y_1 \) respectively. Draw another arc of different radius \( r_2 \) intersecting rays OA and OB at \( X_2 \) and \( Y_2 \) respectively. Let us assume that the lengths of arcs \( X_1Y_1 \) and \( X_2Y_2 \) are \( l_1 \) and \( l_2 \) respectively.
Choose \( n-1 \) points \( P_1, P_2, ..., P_{n-1} \) on the arc \( X_1Y_1 \). These points divide the arc into \( n \) equal parts. Draw radial lines from O to the points \( P_1, P_2, ..., P_{n-1} \) and extend them so that they cut the other arc \( X_2Y_2 \) at points \( Q_1, Q_2, ..., Q_{n-1} \) respectively. Points \( X_1, P_1, P_2, ..., P_{n-1} \) form an open polygon of \( n \) sides.
Now it can be easily proven that \( \triangle OX_1P_1 \sim \triangle OX_2Q_1 \). Similarly \( \triangle OY_1P_{n-1} \sim \triangle OY_2Q_{n-1} \) and \( \triangle OP_kP_{k+1} \sim \triangle OQ_kQ_{k+1} \) for all \( k = 1,2,3,...,n-1 \).
Since corresponding sides are proportional, we get,
\( \frac{X_1P_1}{r_1} = \frac{X_2Q_1}{r_2},\)\( \frac{P_1P_2}{r_1} = \frac{Q_1Q_2}{r_2},\)\( \frac{P_2P_3}{r_1} = \frac{Q_2Q_3}{r_2},\)\( \frac{P_3P_4}{r_1} = \frac{Q_3Q_4}{r_2}, ...,\)\( \frac{P_{n-1}Y_1}{r_1} = \frac{Q_{n-1}Y_2}{r_2} \)
Adding these equations, we get
\( \frac{X_1P_1}{r_1} + \frac{P_1P_2}{r_1} + \frac{P_2P_3}{r_1} + ... + \frac{P_{n-1}Y_1}{r_1} \)\(= \frac{X_2Q_1}{r_2} + \frac{Q_1Q_2}{r_2} + \frac{Q_2Q_3}{r_2} + ... + \frac{Q_{n-1}Y_2}{r_2} \)
\( \Rightarrow \frac{X_1P_1 + P_1P_2 + P_2P_3 + ... + P_{n-1}Y_1}{r_1} \)\(= \frac{X_2Q_1 + Q_1Q_2 + Q_2Q_3 + ... + Q_{n-1}Y_2}{r_2} \)
\( \Rightarrow \frac{\text{Perimeter of open polygon on arc } X_1Y_1}{r_1} \)\(= \frac{\text{Perimeter of open polygon on arc } X_2Y_2}{r_2} \)
If the number of sides of the open polygon \( n \) approaches infinity i.e. \( n \) becomes larger and larger, the perimeter of the open polygon on the arc \( X_1Y_1 \) approaches the limit \( l_1 \) (length of the arc \( X_1Y_1 \)) and the perimeter of the open polygon on the arc \( X_2Y_2 \) approaches the limit \( l_2 \).
Thus, \( \frac{l_1}{r_1} = \frac{l_2}{r_2} \)
Since we had taken two random arcs, if we had drawn an arc of any other radius (say \( r_3 \)) and length (say \( l_3 \)), then \( \frac{l_1}{r_1} = \frac{l_2}{r_2} = \frac{l_3}{r_3} \)
We can conclude that if we draw any arc of any radius between these rays, then
This constant quantity can be used to measure the angle between the rays. If we keep the radius of the arc constant, we see that this constant is directly proportional to the length of the arc. That is, this constant can be said to be proportional to the amount of rotation. When the rays are coinciding, this constant is equal to zero. We define
\( \text{Angle between rays OA and OB} \)\(= \frac{\text{Length of any arc between the rays}}{\text{its radius}} \)
This measurement of angle is called the radian measure or circular measure of angles.
Radian: 1 radian (or written as 1 rad or \( 1^c \)) is the angle made by two rays such that any arc drawn between them has the same length as its radius.
For a complete circle, a similar process (draw a regular polygon of \( n \) sides) can be used to prove that. This constant, when measured, is equal to \( 2\pi \), where \( \pi \) is an irrational number approximately equal to 3.142. Thus circumference of a circle is equal to \( 2\pi r \).
Conversion between Degree Measure and Radian Measure
Radian measure is a very natural way to measure angles using property of a circle. Still, the degree measure is quite prevalent owing to its simplicity. we should know well how to inter-convert both measures.
A circle contains an angle of \(2\pi\) radians which in degrees would have been \(360^\circ\). \(360^\circ\) in circular measure is equal to \(2\pi\) radians, which gives a simple formula to convert radian to degrees and degrees to radians.
And,
To convert an angle in degrees to radians, multiply it with \( \frac{\pi}{180} \) and to convert an angle in radians to degrees, multiply it with \( \frac{180}{\pi} \).
For example: How much is \(30^\circ\) in radians?
Solution: \( 30^\circ = 30 \times \frac{\pi}{180} = \frac{\pi}{6} \)
One must remember, the radian measure of certain special angles in degrees.
| Sr No. | Angle in degrees | Angle in radians | Remarks on how to quickly convert and remember. |
|---|---|---|---|
| 1. | 0° | 0 | |
| 2. | 360° | \(2\pi\) | |
| 3. | 180° | \(\pi\) | Half of 360 |
| 4. | 90° | \(\frac{\pi}{2}\) | 90° is the half of 180°. Thus in radian measure it is \(\frac{\pi}{2}\), which is the half of \(\pi\) |
| 5. | 30° | \(\frac{\pi}{6}\) | One-sixth of 180° |
| 6. | 45° | \(\frac{\pi}{4}\) | Half of 90° |
| 7. | 60° | \(\frac{\pi}{3}\) | One-third of 180° |
| 8. | 120° | \(\frac{2\pi}{3}\) | Twice of 60°, thus, twice of \(\frac{\pi}{3}\) |
| 9. | 150° | \(\frac{5\pi}{6}\) | Five times of 30°, thus, five times of \(\frac{\pi}{6}\) |
| 10. | 210° | \(\frac{7\pi}{6}\) | Seven times of 30° or we may say that it is 180° + 30° i.e. \(\pi + \frac{\pi}{6} = \frac{7\pi}{6}\) |
| 11. | 240° | \(\frac{4\pi}{3}\) | Four times of 60° |
| 12. | 270° | \(\frac{3\pi}{2}\) | Three times of 90° |
| 13. | 300° | \(\frac{5\pi}{3}\) | Five times of 60° |
| 14. | 330° | \(\frac{11\pi}{6}\) | Eleven times of 30° |
| 15. | 15° | \(\frac{\pi}{12}\) | Half of 30° i.e. Half of \(\frac{\pi}{6}\) |
| 16. | 22.5° | \(\frac{\pi}{8}\) | Half of \(\frac{\pi}{4}\) |
| 17. | 18° | \(\frac{\pi}{10}\) | One-tenth of 180° is 18 i.e. One tenth of \(\pi\) |
| 18. | 36° | \(\frac{\pi}{5}\) | Twice of 18° |
| 19. | 72° | \(\frac{2\pi}{5}\) | 72° is 90° - 18° i.e. \(\frac{\pi}{2} - \frac{\pi}{10}\) |
| 20. | 10° | \(\frac{\pi}{18}\) | One-eighteenth of 180° |
Radian is pi
A general confusion in some students occur that an angle in radians must have a \( \pi \) in them e.g., \( \frac{\pi}{6} \), \( \frac{\pi}{2} \), \( 3\pi \) etc. This is not so. The angle in radians can be any number from negative infinity to positive infinity. \( \frac{\pi}{4} \) is a special angle – it is one fourth of a semicircle or one eighth of a circle. Actually \( \frac{\pi}{4} \) is approximately equal to 0.7854.
1 radian equals...
It is helpful to remember that 1 radian is approximately equal to \(57.3^\circ\)
Quadrant of an Angle
Knowing the exact quadrant of terminal point of an angle is important, so that we can decide the correct values of trigonometric functions that we will study later. For instance, suppose you know the angle is \(8\pi\), and you want to also know where the terminal point for this angle is. Since \(8\pi=4*2\pi\) and \(2\pi\) is one complete revolution starting from positive x-axis, we can conclude that \(8\pi\) is \(4\) revolutions and thus the terminal point is at positive x-axis.
To understand this further, read the following points:
-
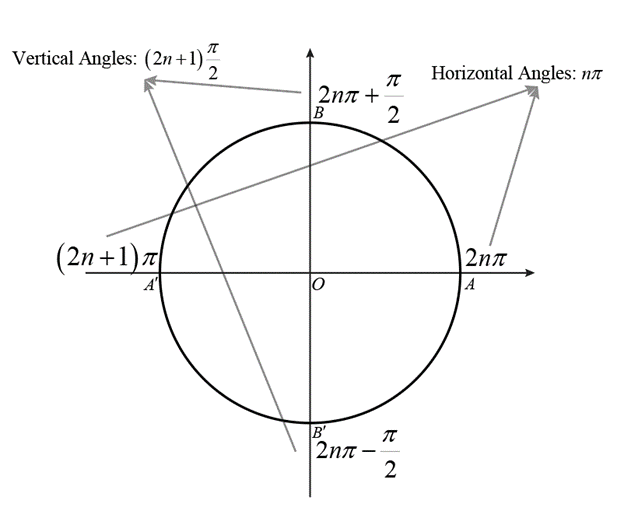
For angles of the form \(2n\pi\), where \(n \in \mathbb{Z}\), the terminal point lies on the positive x-axis. e.g., \( \ldots, -8\pi, -4\pi, -2\pi, 0, 2\pi, 4\pi, 6\pi, 8\pi, \ldots \) all such angles clearly lie on the positive x-axis. It is easy to see that when the angle is of the form \([even\ number] \times \pi\), the angle lies on the positive x-axis.
-
For angles of the form \((2n+1)\pi\), \(n \in \mathbb{Z}\), the terminal point lies on the negative x-axis. Angles like \( \ldots, -7\pi, -5\pi, -3\pi, -\pi, \pi, 3\pi, 5\pi, \ldots \) lie on the negative x-axis. So, whenever the angle is of the form \([odd\ number] \times \pi\), it lies on the negative y-axis.
-
For angles of the form \(2n\pi + \frac{\pi}{2}\), \(n \in \mathbb{Z}\), the terminal point lies on the positive y-axis.
-
For angles of the form \(2n\pi - \frac{\pi}{2}\), \(n \in \mathbb{Z}\), the terminal point lies on the negative y-axis.
-
For angles of the form \(n\pi\), \(n \in \mathbb{Z}\), the terminal point lies either on the positive x-axis or on the negative x-axis. These are called as Horizontal Angles. e.g., \( \ldots, -3\pi, -2\pi, -\pi, 0, \pi, 2\pi, 3\pi, \ldots \)
-
For angles of the form \((2n+1)\frac{\pi}{2}\), \(n \in \mathbb{Z}\), the terminal point lies on the positive y-axis or on the negative y-axis. These are called as Vertical Angles. e.g., \( \ldots, \frac{5\pi}{2}, \frac{3\pi}{2}, \frac{\pi}{2}, -\frac{\pi}{2}, -\frac{3\pi}{2}, -\frac{5\pi}{2}, \ldots \)
Please remember the above results and use the following figure as a memory aid:
Example
Find the location of the terminal point of the following angles:
A) \( \frac{5\pi}{2} \)
Since, \( \frac{5\pi}{2} = 2\pi + \frac{\pi}{2} \) ⇒ it lies on positive y-axis.
B) \( -\frac{57\pi}{2} \)
Since, 57 is an odd number ⇒ it lies on negative x-axis.
C) \( \frac{23\pi}{2} \)
Since, \( \frac{23\pi}{2} = 12\pi - \frac{\pi}{2} \) ⇒ it lies on negative y-axis
D) \( \frac{45\pi}{2} \)
Since, \( \frac{45\pi}{2} = 22\pi + \frac{\pi}{2} \) ⇒ it lies on positive y-axis
If you have understood the above examples, you can easily understand the next concept.
Let us take an example. Suppose \( \theta = \frac{25\pi}{3} \) . We wish to know the quadrant of \( \theta \). Find the multiple of denominator 3 which is the closest to 25 . Write 25 in terms of that multiple.
i.e. \( \frac{25\pi}{3} = \left(24+1\right)\frac{\pi}{3} = 8\pi + \frac{\pi}{3} \)
Now we can tell the correct quadrant in which \( \frac{25\pi}{3} \) lies. Since, \( 8\pi \) lies on positive x-axis. We add \( \frac{\pi}{3} \) to it. Thus the terminal point moves anticlockwise and it lies in the first quadrant.
That’s it. This is what we do.
Let us take more examples.
Example
Find the quadrant of the following angles.
A) \( \frac{27\pi}{7} \)
B) \( \frac{98\pi}{3} \)
C) \( \frac{36\pi}{5} \)
D) \( -\frac{36\pi}{5} \)
Solution:
A) \( \frac{27\pi}{7} = (28-1)\frac{\pi}{7} = 4\pi - \frac{\pi}{7} \)
\( 4\pi \) lies on positive x-axis. Thus \( 4\pi - \frac{\pi}{7} \) lies in fourth quadrant (the terminal point gets rotated by \( \frac{\pi}{7} \) in clockwise direction)
B) \( \frac{98\pi}{3} = (99-1)\frac{\pi}{3} = 33\pi - \frac{\pi}{3} \)
\( 33\pi \) lies on negative x-axis. Thus, \( 33\pi - \frac{\pi}{3} \) lies in the second quadrant. (rotate clockwise)
C) \( \frac{36\pi}{5} = (35+1)\frac{\pi}{5} = 7\pi + \frac{\pi}{5} \)
\( 7\pi \) lies on negative x-axis. Thus \( 7\pi + \frac{\pi}{5} \) lies in the third quadrant. (rotate anticlockwise)
D) \( -\frac{36\pi}{5} = -(35+1)\frac{\pi}{5} = -7\pi - \frac{\pi}{5} \)
\( -7\pi \) lies on negative x-axis. Thus \( -7\pi - \frac{\pi}{5} \) lies in the second quadrant. (rotate clockwise)