Equation of a Straight Line
Equation of Horizontal and Vertical Lines
The equation of a horizontal line in the Cartesian coordinate system can be described by a constant \( y \)-coordinate since all points on the line have the same vertical position. Thus, the general equation of a horizontal line is:
where \( k \) is the \( y \)-coordinate of any point on the line.
The equation of a vertical line, conversely, is given by a constant \( x \)-coordinate, as all points on the line share the same horizontal position. The general equation of a vertical line is:
where \( h \) is the \( x \)-coordinate of any point on the line.
Example
Find the equations of the vertical and horizontal lines that pass through the point \((-1, 3)\) in the Cartesian coordinate system.
Solution: If a vertical line and a horizontal line pass through the point \((-1, 3)\), their equations are as follows:
The equation of the vertical line, which has a constant \( x \)-coordinate, is:
The equation of the horizontal line, with a constant \( y \)-coordinate, is:
These equations represent the vertical and horizontal lines passing through the point \((-1, 3)\) in the Cartesian coordinate system.
Equation of a line with given slope and a point on it
The equation of a line with slope \( m \) passing through a given point \( A(x_1, y_1) \) is \( y - y_1 = m(x - x_1) \).
Proof:
Let \( P(x, y) \) be an arbitrary point on the line other than \( A \). By the definition of the slope, which is the ratio of the change in \( y \) to the change in \( x \) between two distinct points on a line, the slope between points \( A \) and \( P \) is:
Given that the slope of the line is \( m \), and the slope between any two points on a line is constant, we equate the slope \( m \) with \( m_{AP} \):
Multiplying both sides by \( (x - x_1) \) to clear the fraction yields:
This is the point-slope form of the equation of a line, demonstrating that the slope \( m \) and the point \( A(x_1, y_1) \) determine the line. Hence, the equation \( y - y_1 = m(x - x_1) \) must hold for all points \( P(x, y) \) on the line, completing the proof.
Example
Find the equation of a line that makes a \(120^\circ\) angle with the positive x-axis and passes through the point \((-2, 3)\).
Solution:
The slope \(m\) of a line that forms a \(120^\circ\) angle with the positive x-axis can be calculated using the tangent of the angle, as the slope is the tangent of the inclination:
Since \(\tan(120^\circ) = -\sqrt{3}\), the slope of the line is \(-\sqrt{3}\) because the tangent function is negative in the second quadrant (where \(120^\circ\) lies).
Using the point-slope form of the line equation, \(y - y_1 = m(x - x_1)\), where \(m\) is the slope and \((x_1, y_1)\) is a point on the line, we substitute \(m = -\sqrt{3}\) and \((-2, 3)\) for \((x_1, y_1)\):
This equation can be simplified or rearranged depending on the preferred format; however, it correctly represents the line's equation as it stands.
Equation of a line joining two points
The equation of a line passing through two distinct points \( A(x_1, y_1) \) and \( B(x_2, y_2) \) is given by \( y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \).
Proof:
Let the slope \( m \) of the line connecting points \( A \) and \( B \) be defined by the change in \( y \)-coordinates divided by the change in \( x \)-coordinates between these two points. Thus, the slope \( m \) is calculated as:
This formula for the slope stems from the definition of slope in the Cartesian coordinate system, representing the rate of change of \( y \) with respect to \( x \) along the line.
Given the point-slope form of the equation of a line, which states that the difference in the \( y \)-coordinates of any point \( (x, y) \) on the line and point \( A \) is proportional to the difference in their \( x \)-coordinates, scaled by the slope \( m \), we express this relationship as:
Substituting the expression for \( m \) into the point-slope form yields:
This equation confirms that any point \( (x, y) \) satisfying this equation will lie on the line through \( A \) and \( B \), thus proving that it is the equation of the line joining points \( A \) and \( B \). The equation is valid provided that \( x_1 \neq x_2 \), ensuring that the denominator is non-zero and the slope is defined.
Alternative form
A line passing through two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\) is given by:
Proof:
Let \(P(x,y)\) be an arbitrary point on the line joining \(A\) and \(B\).
The area of a triangle formed by three points in a Cartesian plane can be calculated using the determinant of a matrix formed by their coordinates. For the points \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(P(x, y)\), the formula for the area is given by:
Since the points are collinear, the area \(\Delta\) must be zero. Therefore, we set the determinant to zero:
Intercept of a line on axes
If a line intersects the x-axis at the point \((a, 0)\), then the x-axis intercept is simply referred to as \(a\). This value represents the point along the x-axis where the line crosses. Similarly, if the line intersects the y-axis at the point \((0, b)\), then the y-axis intercept is denoted by \(b\). This value indicates the point along the y-axis where the line crosses. These intercepts, \(a\) and \(b\), provide a concise way to describe the behavior of the line in relation to each axis.
Slope-Intercept form of a Line
The slope-intercept form of a line is a way to express the equation of a straight line when its slope \(m\) and y-intercept \(c\) are known. This form is represented as:
Here, \(m\) represents the slope of the line, and \(c\) represents the y-coordinate of the point where the line intersects the y-axis, commonly referred to as the y-intercept.
Proof:
Consider a line with a known slope \(m\) that passes through the y-axis at the point \((0, c)\). The slope \(m\) is defined as the ratio of the change in the y-coordinates to the change in the x-coordinates between any two points on the line. Specifically, if you have a point \((x, y)\) on the line and another point \((0, c)\) on the line (the y-intercept), the slope \(m\) can be calculated as follows:
Rearranging this equation to solve for \(y\) gives:
This confirms that the line's equation is \(y = mx + c\). This form is particularly useful because it provides a straightforward method to graph the line by starting at the y-intercept \((0, c)\) and using the slope \(m\) to determine the rise over run, moving from the intercept to other points on the line.
Importance of this form
The slope-intercept form of a line, represented as \( y = mx + c \), is highly significant for us for various reasons:
-
Clarity and Simplicity:
The slope-intercept form directly shows the slope \( m \) and the y-intercept \( c \) of the line. This clarity makes it straightforward to understand and visualize the behavior of the line without additional calculations.
-
Ease of Graphing:
This form simplifies graphing the line. By starting at the y-intercept \( c \) on the y-axis and using the slope \( m \) to determine the rise over run, one can plot subsequent points with ease.
-
Analytical Convenience:
Analyzing relationships between variables in various fields such as physics, economics, and biology often involves linear models. For example you might have seen the equation \(v=u+at\) is physics motion chapter as the motion of a particle under constant acceleration. \(u\) in the initial velocity, \(t\) is the variable time, \(v\) is the velocity at time \(t\) and \(a\) is the constant acceleration. If you will plot the graph of \(v\) versus \(t\), then \(u\) is the y-intercept and \(a\) is the slope of the line.
Example
Example:
Consider two points on a line, \( A(1, 2) \) and \( B(4, 6) \).
Step 1: Calculate the slope \(m\).
The slope between two points is given by the formula:
Substituting the coordinates of points \(A\) and \(B\):
Step 2: Use the point-slope form to write the equation of the line.
With the slope \(m\) and point \(A(1, 2)\) known, the point-slope form is:
Step 3: Convert to slope-intercept form \(y = mx + c\).
Solving for \(y\) gives:
Conclusion:
The equation of the line passing through points \(A\) and \(B\) in slope-intercept form is \(y = \frac{4}{3}x + \frac{2}{3}\). This form is particularly useful as it directly reveals the slope \(m = \frac{4}{3}\) and the y-intercept \(c = \frac{2}{3}\), facilitating a straightforward understanding of the line's behavior and easy graphing.
Slope and x-intercept are known
If a line has a known slope \( m \) and an x-intercept \( a \), the equation of the line can be expressed as \( y = m(x-a) \).
Proof:
Consider the general point-slope form of a line equation, where \( (x_1, y_1) \) is any point on the line, and \( m \) is the slope:
For a line with an x-intercept at \( a \), the point \( (a, 0) \) lies on the line. Substituting \( x_1 = a \) and \( y_1 = 0 \) into the point-slope equation, we obtain:
This simplifies directly to:
This derivation confirms that the line equation \( y = m(x - a) \) correctly represents a line with slope \( m \) passing through the x-intercept \( a \), thus concluding the proof. \(\blacksquare\)
Intercept form of the Line
If a line has known x-intercept \(a\) and y-intercept \(b\), then the equation of the line can be expressed in intercept form as:
Proof:
Given that the line intercepts the x-axis at \(a\) and the y-axis at \(b\), it passes through the points \((a, 0)\) and \((0, b)\). We can derive the equation of the line using these intercepts.
-
Use the two-point form of a line equation:
The general equation of a line passing through two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]Substituting the points \((a, 0)\) and \((0, b)\):
\[ \frac{y - 0}{b - 0} = \frac{x - a}{0 - a} \]Simplifying gives:
\[ \frac{y}{b} = \frac{x - a}{-a} \]\[ \frac{y}{b} = -\frac{x}{a} + 1 \] -
Rearrange to form the intercept equation: Rearranging the equation gives:
\[ \frac{y}{b} = 1 - \frac{x}{a} \]\[ \frac{y}{b} + \frac{x}{a} = 1 \]
\(\blacksquare\)
Example
If a line intersects the x-axis at point \( A(a, 0) \) and the y-axis at point \( B(0, b) \), and a point \( P(\alpha, \beta) \) divides the line segment \( AB \) in the ratio \( m:n \), then the equation of the line can be expressed as:
Proof:
-
Given
- The line's intercept form is given by \( \frac{x}{a} + \frac{y}{b} = 1 \), with \( A = (a, 0) \) and \( B = (0, b) \).
- The point \( P(\alpha, \beta) \) divides \( AB \) in the ratio \( m:n \).
-
Using Section Formula:
-
According to the section formula, the coordinates of \( P \) are determined by:
\[ P = \left( \frac{mB + nA}{m+n} \right) \] -
Substituting \( A = (a, 0) \) and \( B = (0, b) \), the coordinates \( P(\alpha, \beta) \) become:
\[ \alpha = \frac{n \cdot 0 + m \cdot a}{m+n} = \frac{ma}{m+n} \]\[ \beta = \frac{m \cdot 0 + n \cdot b}{m+n} = \frac{nb}{m+n} \]
-
-
Expressing \( a \) and \( b \) in terms of \( \alpha \) and \( \beta \):
-
Rearranging the formulas for \( \alpha \) and \( \beta \) gives:
\[ a = \frac{\alpha(m+n)}{m} \]\[ b = \frac{\beta(m+n)}{n} \]
-
-
Substitute \( a \) and \( b \) into the line's equation:
-
Substituting the expressions for \( a \) and \( b \) back into the line equation \( \frac{x}{a} + \frac{y}{b} = 1 \):
\[ \frac{x}{\frac{\alpha(m+n)}{m}} + \frac{y}{\frac{\beta(m+n)}{n}} = 1 \] -
Simplify this to:
\[ \frac{mx}{\alpha(m+n)} + \frac{ny}{\beta(m+n)} = 1 \] -
Multiply through by \( (m+n) \) to clear the denominator:
\[ \frac{mx}{\alpha} + \frac{ny}{\beta} = m + n \]
-
General Equation of a Straight Line
The general equation of a line in the Cartesian coordinate system is expressed as:
Here, \(a\), \(b\), and \(c\) are constants. This form of the line equation is versatile and can represent any line in a two-dimensional space, including vertical, horizontal, and oblique lines.
\(a\) and \(b\) cannot both be zero simultaneously. This ensures that the equation represents a line and not a degenerate case.
-
Horizontal Line: If \(a = 0\), the equation simplifies to \(by + c = 0\). Rearranging gives \(y = -\frac{c}{b}\), which is the equation of a horizontal line parallel to the x-axis.
-
Vertical Line: If \(b = 0\), the equation simplifies to \(ax + c = 0\). Rearranging yields \(x = -\frac{c}{a}\), representing a vertical line parallel to the y-axis.
-
Line Passing Through the Origin: If \(c = 0\), the equation reduces to \(ax + by = 0\), indicating that the line passes through the origin (0,0).
-
Slope of the Line: The slope \(m\) of the line can be derived by rearranging the line equation into slope-intercept form \(y = mx + n\). Starting from \(ax + by + c = 0\) and solving for \(y\), we obtain \(y = -\frac{a}{b}x - \frac{c}{b}\). Therefore, the slope \(m\) of the line is \(-\frac{a}{b}\).
-
X-intercept: To find the x-intercept, set \(y = 0\) in the general equation:
\[ ax + by + c = 0 \implies ax + c = 0 \implies x = -\frac{c}{a}. \]Hence, the x-intercept is \((- \frac{c}{a}, 0)\).
-
Y-intercept: To find the y-intercept, set \(x = 0\) in the general equation:
\[ ax + by + c = 0 \implies by + c = 0 \implies y = -\frac{c}{b}. \]Therefore, the y-intercept is \((0, - \frac{c}{b})\).
In summary, the line described by the equation \(ax + by + c = 0\) has characteristics that depend on the coefficients \(a\), \(b\), and \(c\). It may be horizontal, vertical, or have a negative reciprocal slope depending on the values of \(a\) and \(b\). The line intersects the x-axis and y-axis at calculated points unless it is parallel to one of the axes.
Parallel and perpendicular Lines
Consider two lines \(L_1\) and \(L_2\) given by the equations:
Parallel Lines:
For the lines \(L_1\) and \(L_2\) to be parallel, their slopes must be equal. The slope of a line \(ax + by + c = 0\) is given by \(-\frac{a}{b}\) (provided \(b \neq 0\)). Therefore, the slopes of \(L_1\) and \(L_2\) are \(-\frac{a_1}{b_1}\) and \(-\frac{a_2}{b_2}\) respectively. Setting these slopes equal gives:
Thus, for \(L_1\) and \(L_2\) to be parallel, \(\frac{a_1}{a_2} = \frac{b_1}{b_2}\).
Coincident Lines:
Lines \(L_1\) and \(L_2\) are coincident if they are not only parallel but also have the same y-intercept. This condition is met if the entire equations are proportional, i.e., \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\). This proportionality ensures that every point on \(L_1\) also lies on \(L_2\), and vice versa, indicating that the two lines are indeed the same (coincident).
Perpendicular Lines:
Two lines are perpendicular if the product of their slopes is \(-1\). From the slope expressions derived, the product of the slopes of \(L_1\) and \(L_2\) is:
Setting this equal to \(-1\) for perpendicularity, we have:
Therefore, for \(L_1\) and \(L_2\) to be perpendicular, \(a_1a_2 + b_1b_2 = 0\).
A neat way to write parallel and perpendicular lines
-
Consider the equation of a line in the form \( ax + by + c = 0 \). A line parallel to this can be represented by altering the constant term while keeping the coefficients of \( x \) and \( y \) unchanged. Thus, the equation of a parallel line is given by \( ax + by + \lambda = 0 \), where \( \lambda \) is a constant different from \( c \). The value of \( \lambda \) can be determined based on additional information related to specific conditions or constraints in the problem context.
-
A line perpendicular to the equation \( ax + by + c = 0 \) can be formulated by altering the coefficients of \( x \) and \( y \) and changing the sign of one of them to ensure the slopes are negative reciprocals of each other. This results in the equation \( bx - ay + \lambda = 0 \), where \( \lambda \) is a constant that can be determined based on additional specific information or constraints. This relationship ensures that the product of the slopes of the two lines is \(-1\), confirming their perpendicularity.
-
The equation of a line parallel to \( ax + by + c = 0 \) passing through a point \((x_1, y_1)\) is derived by ensuring the line has the same coefficients of \(x\) and \(y\) but passes through the given point. The general form of the line equation, \(ax + by + d = 0\), is adjusted to pass through \((x_1, y_1)\) by substituting these coordinates and solving for \(d\). This yields \(d = -ax_1 - by_1\). Thus, the equation of the line becomes:
\[ a(x - x_1) + b(y - y_1) = 0 \]Similarly, a line perpendicular to \(ax + by + c = 0\) and passing through \((x_1, y_1)\) must have coefficients that result in a slope that is the negative reciprocal of the original line. This is achieved by switching the coefficients of \(x\) and \(y\) and changing the sign of one. Substituting \((x_1, y_1)\) into the perpendicular line equation \(bx - ay + d = 0\) to find \(d\) results in \(d = -bx_1 + ay_1\). Therefore, the equation of the perpendicular line is:
\[ b(x - x_1) - a(y - y_1) = 0 \]
Intersection of two lines
To determine the intersection point of two lines given by their equations \( L_1: a_1x + b_1y + c_1 = 0 \) and \( L_2: a_2x + b_2y + c_2 = 0 \), we consider three scenarios:
I. Parallel but not Coincident Lines:
For two lines to be parallel but not coincident, they must have the same slope but different y-intercepts. This condition is represented by \( \frac{a_1}{a_2} = \frac{b_1}{b_2} \) and \( \frac{a_1}{a_2} \neq \frac{c_1}{c_2} \). In this case, there is no intersection point as the lines are parallel and distinct.
II. Coincident Lines:
Lines are coincident when \( \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} \). This implies that every point on \( L_1 \) is also on \( L_2 \), leading to infinitely many intersection points, essentially all points on either line.
III. Not Parallel Lines (Intersecting Lines):
When lines are not parallel, they will intersect at a unique point. The condition for non-parallel lines is \( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \), which ensures that the determinant of the coefficient matrix is non-zero. The determinant is given by \( D = a_1b_2 - a_2b_1 \). If \( D \neq 0 \), the lines will intersect at a unique point. The coordinates \((x, y)\) of the intersection point can be found using cross-multiplication method:
Concurrency of three lines
Three lines \( L_1: a_1x + b_1y + c_1 = 0 \), \( L_2: a_2x + b_2y + c_2 = 0 \), and \( L_3: a_3x + b_3y + c_3 = 0 \) are concurrent (intersect at a single point) if and only if the determinant of their coefficient matrix is zero:
Proof:
Assume that the lines \( L_1 \), \( L_2 \), and \( L_3 \) are concurrent. This implies there exists a point \((x, y)\) that simultaneously satisfies all three line equations.
-
Intersection of \( L_1 \) and \( L_2 \): Calculate the intersection point of \( L_1 \) and \( L_2 \) using Cramer's Rule. For non-parallel lines, the intersection point \((x, y)\) can be derived as follows:
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]where \( D = a_1b_2 - a_2b_1 \neq 0 \) (since \( L_1 \) and \( L_2 \) are not parallel).
-
Substitute into \( L_3 \): Substitute \( x \) and \( y \) into \( L_3 \) to see if the point lies on the third line:
\[ a_3 \left(\frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}\right) + b_3 \left(\frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1}\right) + c_3 = 0 \]Simplifying, this can be rewritten in matrix form:
\[ \frac{1}{a_1b_2 - a_2b_1} \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} = 0 \]Given the equation \( \frac{1}{D} \times \text{Determinant} = 0 \) holds true, the determinant must be zero for the equation to hold, confirming that:
\[ \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} = 0 \]
Normal form the line
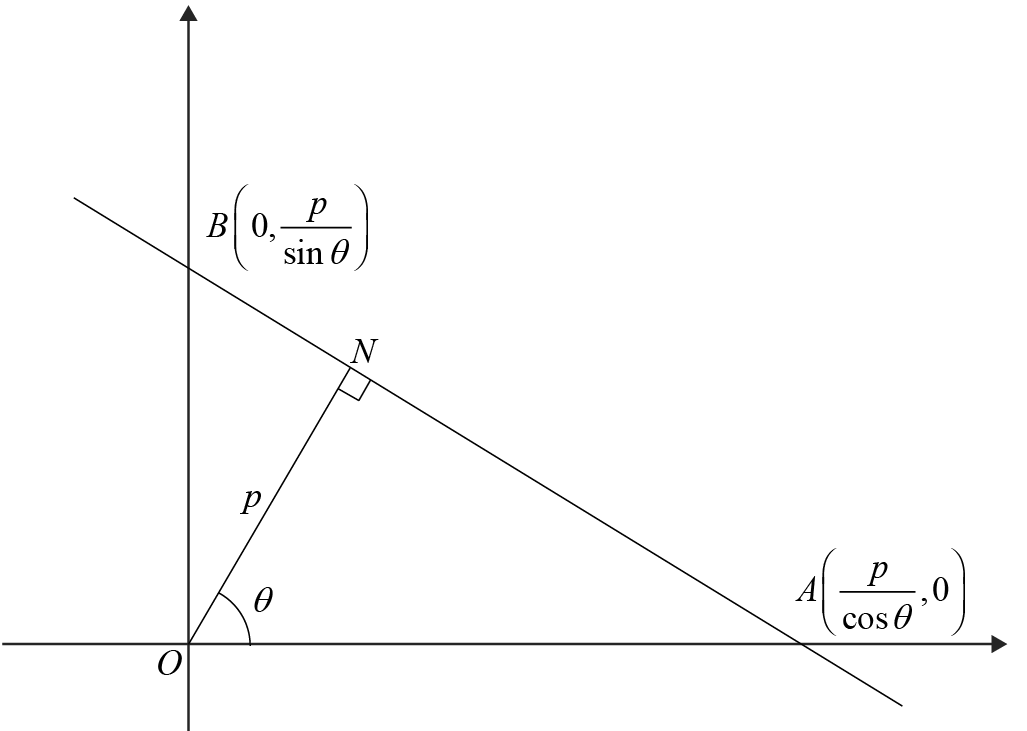
The normal form of the equation of a straight line is \(x \cos \theta + y \sin \theta = p\), where \(p\) is the perpendicular distance from the origin to the line, and \(\theta\) is the angle the normal makes with the positive x-axis.
Proof:
To derive this form, consider a line that cuts the x-axis at point \(A\) and the y-axis at point \(B\). Let the foot of the perpendicular dropped from the origin \(O\) to the line be \(N\), making \(ON = p\) and \(\theta\) the angle \(ON\) makes with the positive x-axis.
-
Axis Intercepts:
- In triangle \(OAN\), the angle at \(O\) is \(\theta\), \(ON = p\) is the length of the perpendicular from the origin to the line, and \(OA\) is along the x-axis.
-
Using the definition of cosine in triangle \(OAN\), we have:
\[ \cos \theta = \frac{ON}{OA} \implies OA = \frac{ON}{\cos \theta} = \frac{p}{\cos \theta} \]Thus, the x-intercept \(A\) is \(\left(\frac{p}{\cos \theta}, 0\right)\).
-
In triangle \(OBN\), the angle at \(O\) is \(90^\circ - \theta\), and \(OB\) is along the y-axis.
-
Using the definition of sine in triangle \(OBN\), we find:
\[ \sin \theta = \frac{ON}{OB} \implies OB = \frac{ON}{\sin \theta} = \frac{p}{\sin \theta} \]Therefore, the y-intercept \(B\) is \(\left(0, \frac{p}{\sin \theta}\right)\).
-
Derivation of Line Equation via Intercept Form:
- The intercept form of a line's equation is \(\frac{x}{a} + \frac{y}{b} = 1\), where \(a\) and \(b\) are the x- and y-intercepts, respectively.
-
Substituting \(a = \frac{p}{\cos \theta}\) and \(b = \frac{p}{\sin \theta}\), the line equation becomes:
\[ \frac{x}{\frac{p}{\cos \theta}} + \frac{y}{\frac{p}{\sin \theta}} = 1 \implies \frac{x \cos \theta}{p} + \frac{y \sin \theta}{p} = 1 \] -
Multiplying through by \(p\), we obtain:
\[ x \cos \theta + y \sin \theta = p \]
Symmetric Form of a Straight Line
The symmetric form of a line is a useful representation that captures the orientation and position of a line in a coordinate plane. It is given by the equation:
Here, \((x_1, y_1)\) is a known point through which the line passes, \(\theta\) is the angle the line makes with the positive x-axis, and \(r\) is the parameter representing the signed distance from the point \((x_1, y_1)\) to any point \((x, y)\) on the line. \(|r|\) is the actual distance between \((x_1, y_1)\) and \((x, y)\).
Proof:
Consider the straight line containing the fixed point \( A(x_1, y_1) \) and an arbitrary point \( P(x, y) \). Construct the right angled triangle \(APN\). The \( \angle NAP = \theta \). By the definition of cosine and sine in a right-angled triangle:
From these equations, we can deduce:
Which implies:
If point \( P \) is situated below \( A \), the signs of the components change, giving us \( AN = x_1 - x \) and \( PN = y_1 - y \), which results in:
Leading to:
Therefore, for any arbitrary point \( P \) on the line, we establish that:
Here, \( r \) is a positive number representing the distance from \( A \) to \( P \). The \( \pm \) symbol accounts for the fact that \( r \) can be oriented in either direction along the line. We replace \(\pm r\) by just \(r\) (absorbing \(\pm\) in \(r\)). Now, \( r \) can be considered a signed distance, where the sign indicates the direction with respect to the fixed point \( A \). Consequently, \( |r| \) gives the absolute distance from \( A \) to \( P \) without concern for direction. \(\blacksquare\)
When to use this form
The symmetric form of the equation of a line is particularly useful in measuring distances along the line from a fixed point. This form is expressed as:
where \( (x_1, y_1) \) is a point on the line, \( \theta \) is the angle the line makes with the x-axis, and \( r \) is the signed distance from the fixed point to any other point \( (x, y) \) on the line.
Example
Problem: Determine the coordinates of a point which lies at a distance of 5 units from the fixed point \( (1, -2) \) on the line \( 3x + 4y + 5 = 0 \).
Solution: Convert the given line equation to its symmetric form.
Given the equation of the line \(3x + 4y + 5 = 0\), we are to find the coordinates of a point that lies 5 units away from the fixed point \( (1, -2) \) on the line.
The slope of the line is the negative coefficient of \( x \) divided by the coefficient of \( y \), which gives \(\tan(\theta) = -\frac{3}{4}\). The negative value of \(\theta\) indicates that \(\theta\in\left(\frac{\pi}{2}, \pi\right)\). So, \(\cos\theta\) must be taken negative and \(\sin\theta\) is positive.
We substitute these values into the symmetric form equation \( \frac{x - x_1}{\cos(\theta)} = \frac{y - y_1}{\sin(\theta)} = r \), with \( x_1 = 1 \), \( y_1 = -2 \), and \( r = \pm 5 \), obtaining:
Solving for \( x \) and \( y \) gives us:
Therefore, the two possible points on the line that are 5 units away from \( (1, -2) \) are \( (-3, 1) \) and \( (5, -5) \).