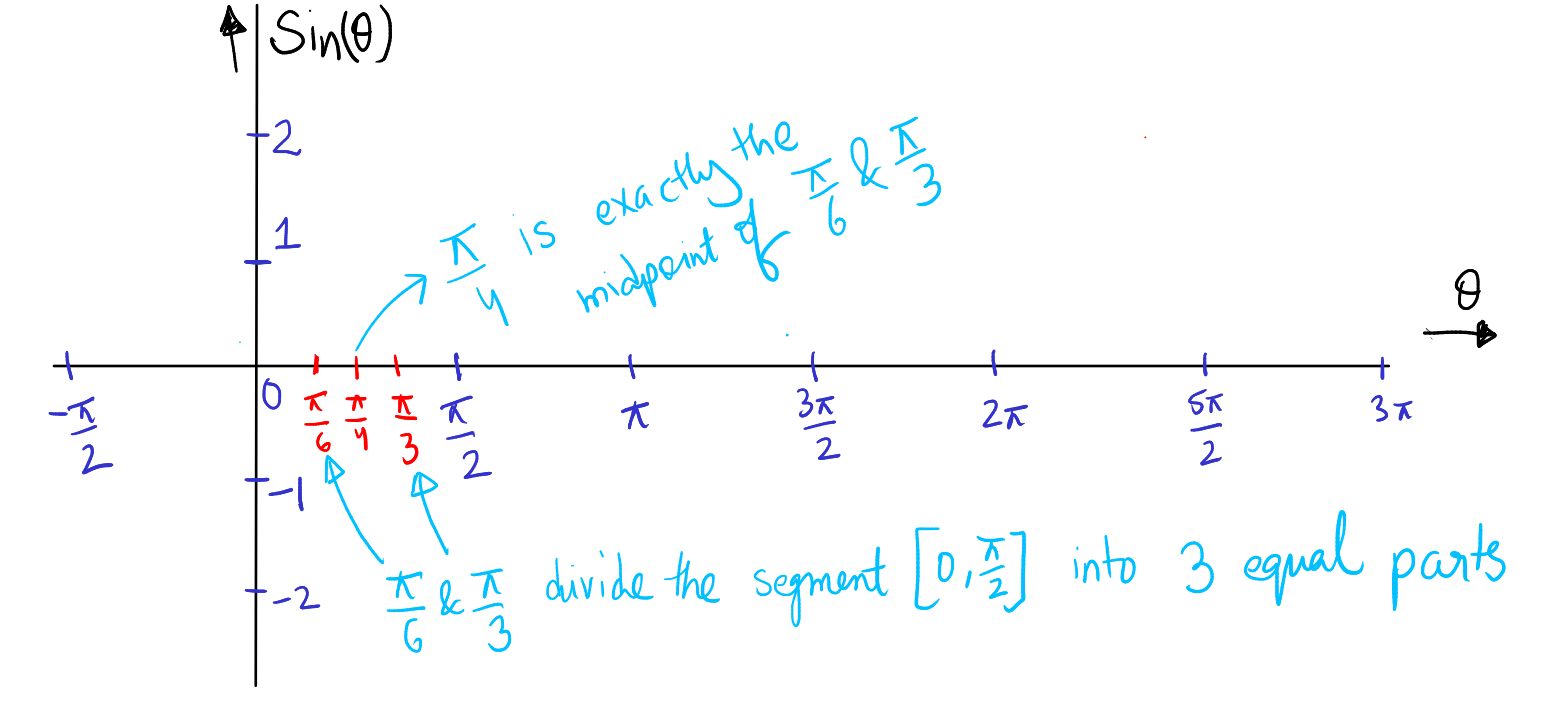Drawing Graphs
An introduction
As a point \( P \) traces the path of a unit circle, it encounters the same points repeatedly after completing each full rotation. This recurring journey around the circle results in the trigonometric functions—such as sine and cosine—exhibiting a pattern of repetition known as periodicity. To put it simply, if we take the sine of an angle \( \theta \), represented as \( \sin(\theta) \), and find that its value is \( y \), then after the point \( P \) completes one full circle (which corresponds to an angle of \( 2\pi \) radians), the sine of the new angle, \( \theta + 2\pi \), will also be \( y \).
This concept can be visualized on a graph that plots the sine value against its angle. As the angle increases by \( 2\pi \) radians, the sine value will follow the same path as before, creating a wave-like pattern that rises and falls. The distance over which this pattern repeats, which in the case of sine and cosine is \( 2\pi \) radians, is called the period of the function. In essence, the period is the angular distance after which the trigonometric functions start to echo their previous values, illustrating their inherent cyclical nature. This property is what allows these functions to model periodic phenomena so effectively, such as the oscillations of a pendulum or the waves of the sea.
The Graph of Sine
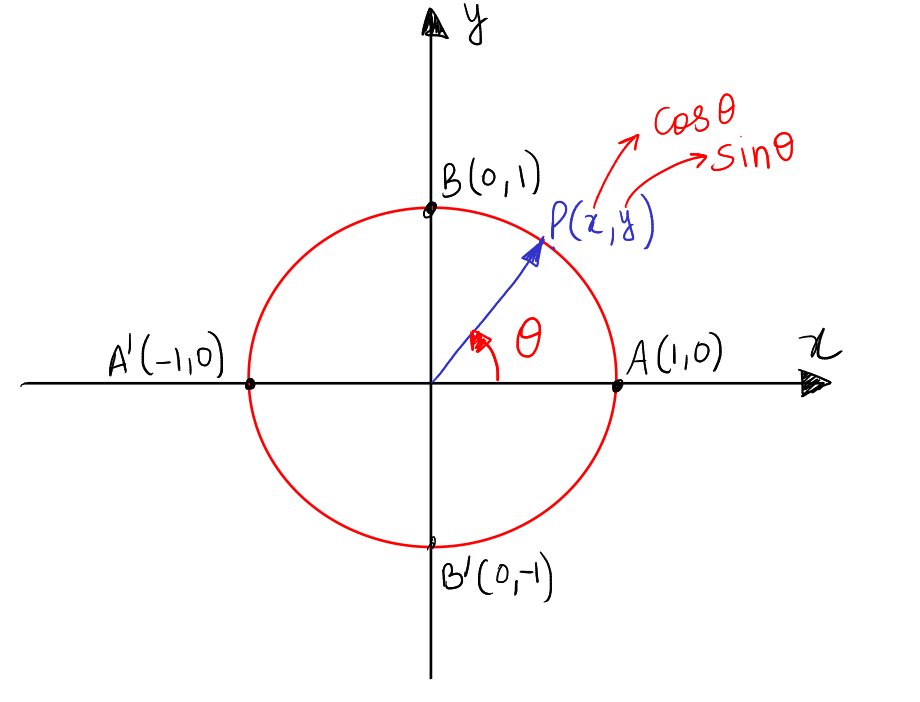
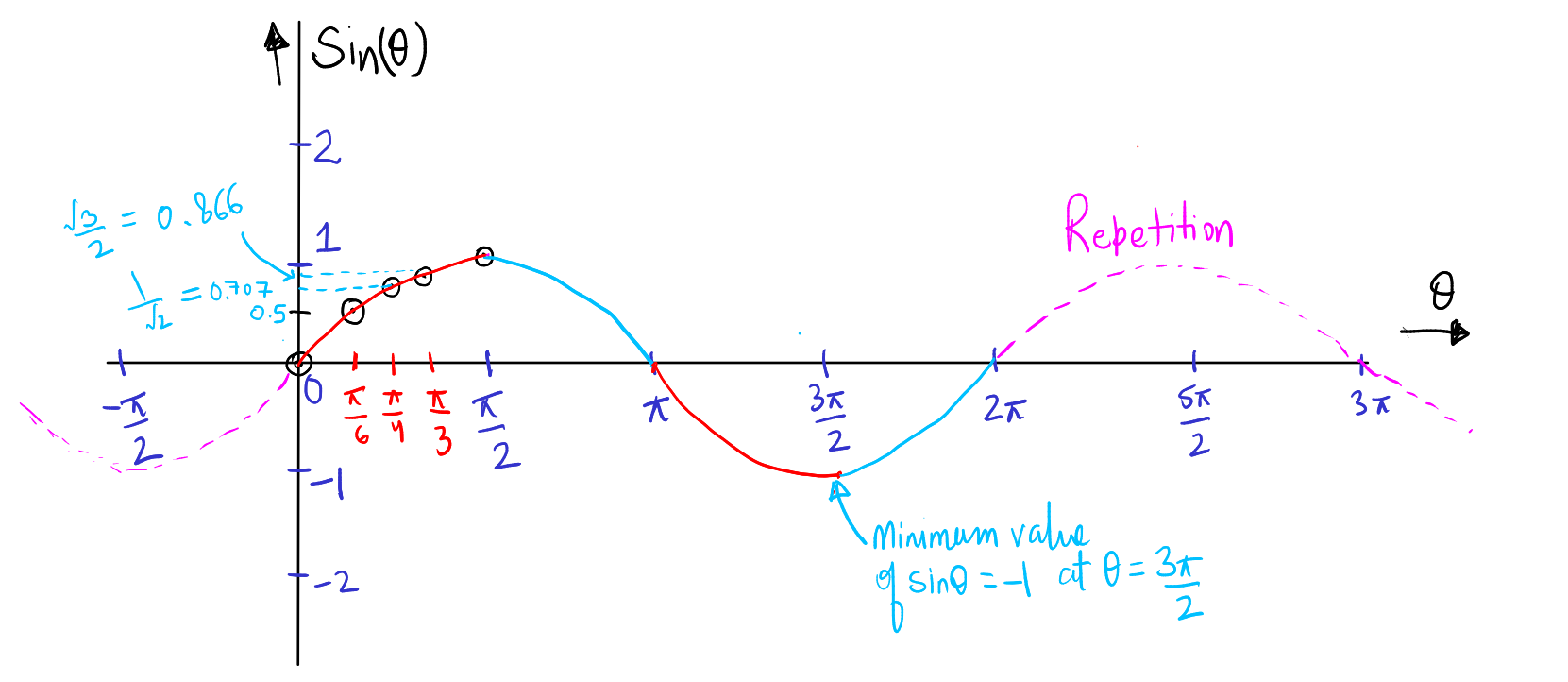
The sine function relates an angle with the vertical component(ordinate) of a point located on the unit circle's circumference. Look at the image below. Point \(P\) moves on the circumference of the unit circle with coordinates \((x,y)\). Angle \(AOP\) is \(\theta\). Focus on \(y\), which we know is the sine of angle \(\theta\). Imagine this point, starting from point \(A\) with coordinates \((1,0)\), moving on this circle.
-
At \(A\) the value of sine is clearly \(0\). As it moves further the value of sine (ordinate of P) starts increasing to 1, and it becomes 1 when \(\theta=\frac{\pi}{2}\). Keep moving point \(P\) like this around the circle and read the value of the its ordinate for each value of \(\theta\).
-
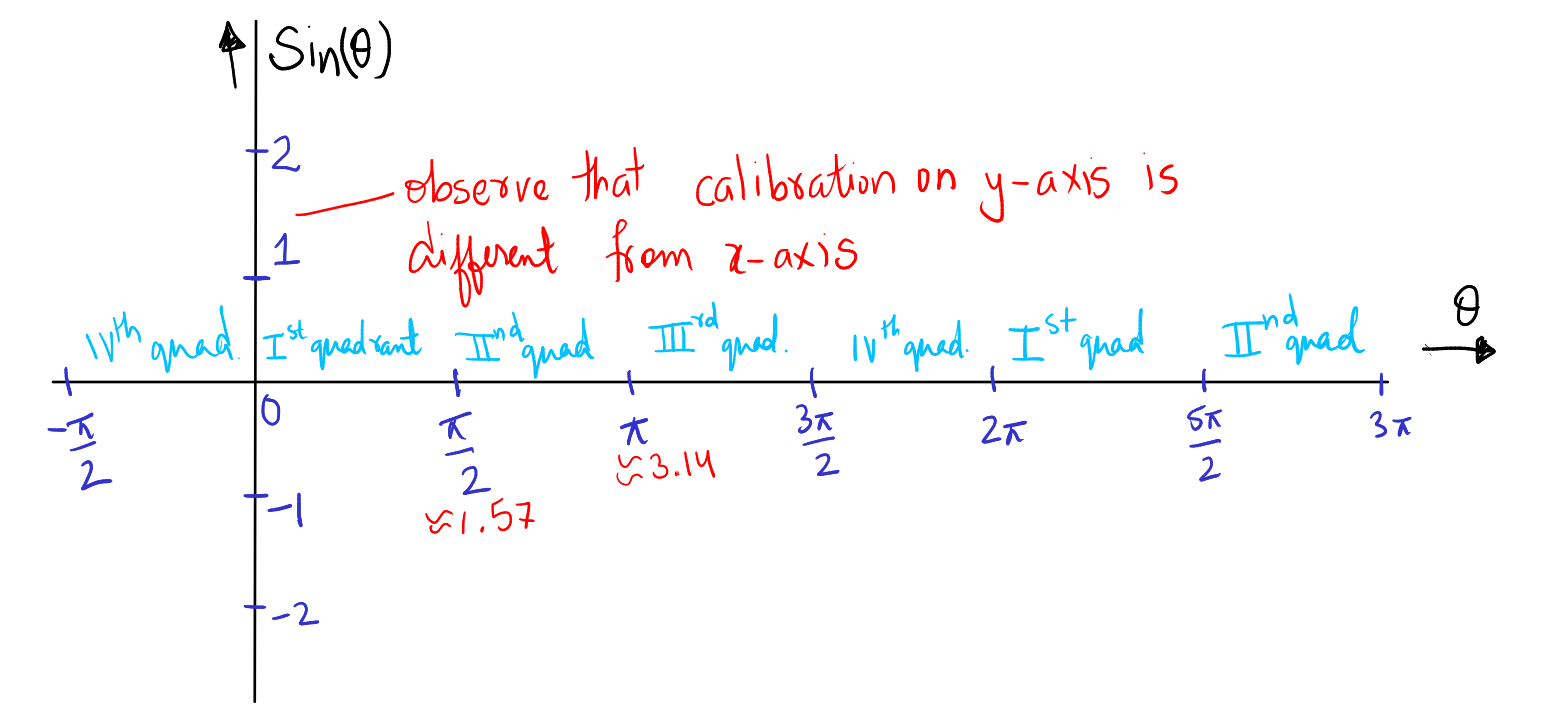
It then reaches second quadrant, where theta changes from \(\frac{\pi}{2}\) to \(\pi\) and if you observe carefully, the value of sine, i.e. the ordinate of \(P\) decreases from \(1\) to \(0\).
-
\(P\) then moves to third quadrant, \(\theta\) changes from \(\pi\) to \(\frac{3\pi}{2}\). Correspondingly, \(\sin\theta\) decreases from \(0\) to \(-1\).
-
Eventually, \(P\) reaches the fourth quadrant, where \(\theta\) changes from \(\frac{3\pi}{2}\) to \(2\pi\) and correspondingly \(sin\theta\) increases from \(-1\) to \(0\).
-
As \(P\) moves further anti-clockwise, it is again in first quadrant. Now \(\theta\) changes from \(2\pi\) to \(\frac{5\pi}{2}\). \(sin\theta\) again increased from \(0\) to \(1\).
-
This cycle keeps on repeating and the value of \(sin\theta\) oscillates between \(-1\) to \(1\).
Procedure for Plotting the Graph of Sine Function
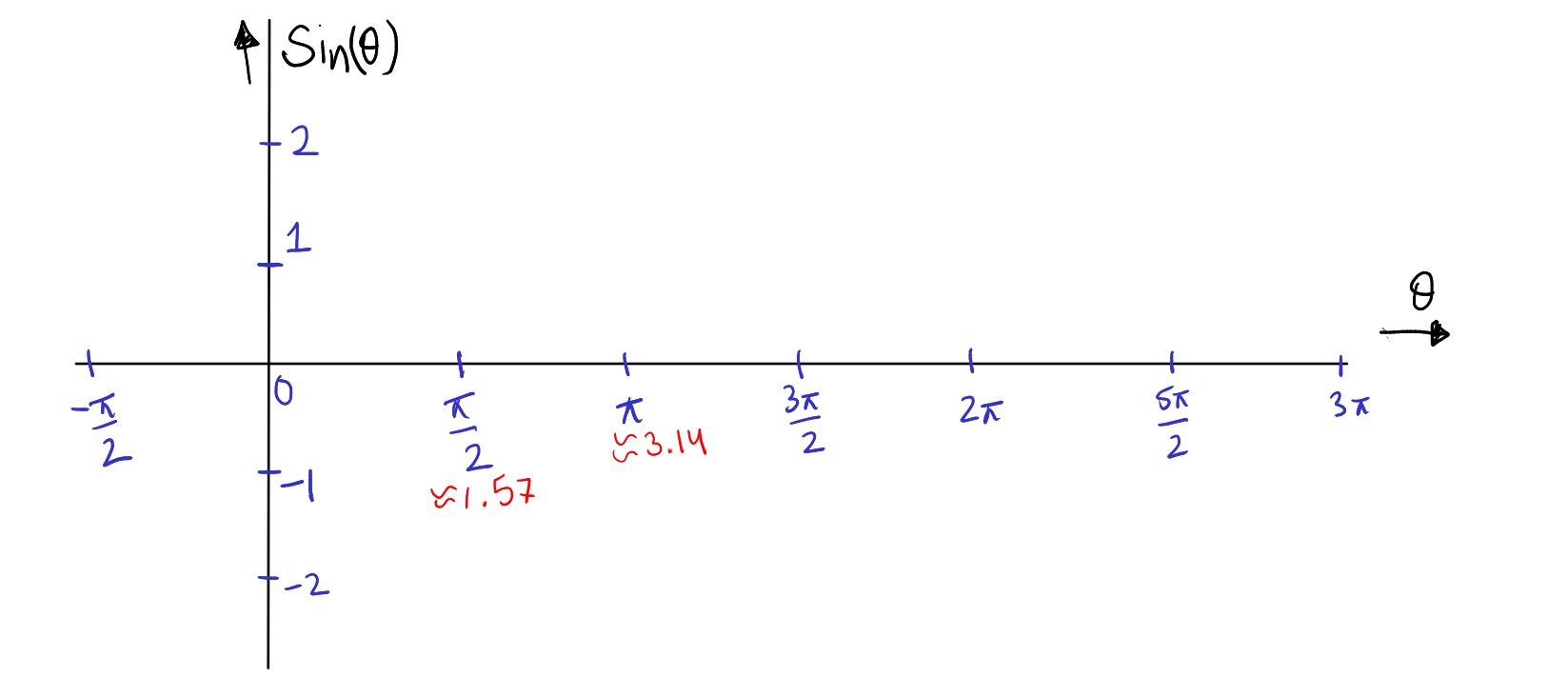
Step 1: Preparation of the Axes To begin plotting \( \sin \theta \) against \( \theta \), draw two perpendicular lines to establish the x-axis (for \( \theta \)) and the y-axis (for \( \sin \theta \)). The range of \( \sin \theta \) is from -1 to 1.
Step 2: Scaling the x-axis and y-axis Divide the x-axis into units where each unit corresponds to \( \pi/2 \) radians. The segment between 0 to \( \pi/2 \) radians denotes the first quadrant of the unit circle. Calibrate the y-axis in integers as the range is \([-1,1]\), on y-axis.
Note
Observe that \(\frac{\pi}{2}\approx 1.57\). We do not use integer scaling on x-axis because it would then become difficult to locate 1.57 on it. All special angles are in the form of \(\frac{p\pi}{q}\). So calibration in terms of \(\frac{\pi}{2}\) is a natural choice.
Step 3: Plotting Points in the First Quadrant At \( \theta = 0 \), plot the initial point where \( \sin \theta = 0 \). Continue to mark the sine values at \( \theta = \pi/6, \pi/3, \) and \( \pi/2 \). Note that \( \pi/4 \) is the midpoint between \( \pi/6 \) and \( \pi/3 \). Use the table below. Plot the ordered pair \( (\theta, \sin(\theta)) \) on the cartesian coordinate system that you made in step 2 above.
| \( \theta \) | \( \sin(\theta) \) | Ordered Pair \( (\theta, \sin(\theta)) \) |
|---|---|---|
| 0 | 0 | \( (0, 0) \) |
| \( \frac{\pi}{6} \) | \( \frac{1}{2} \) | \( (\frac{\pi}{6}, \frac{1}{2}) \) |
| \( \frac{\pi}{4} \) | \( \frac{\sqrt{2}}{2} \) | \( (\frac{\pi}{4}, \frac{\sqrt{2}}{2}) \) |
| \( \frac{\pi}{3} \) | \( \frac{\sqrt{3}}{2} \) | \( (\frac{\pi}{3}, \frac{\sqrt{3}}{2}) \) |
| \( \frac{\pi}{2} \) | 1 | \( (\frac{\pi}{2}, 1) \) |
Step 4: Reflecting the Curve for the Second Quadrant Recognize the symmetry of the unit circle and reflect the plotted points across the second quadrant. Here, as \( \theta \) advances from \( \pi/2 \) to \( \pi \), the sine value gradually returns to 0.
Step 5: Extending the Curve to the Third and Fourth Quadrants Proceed to the third quadrant, marking the declining sine values until they reach -1 at \( \theta = 3\pi/2 \). In the fourth quadrant, plot the increasing sine values, which rise back to 0 at \( \theta = 2\pi \).
Step 6: Completion of the Sine Wave Join all the points with a smooth, flowing line to create a wave pattern, which represents the sine function's periodic nature.
Conclusion Upon completing the graph, one will observe the periodic and oscillatory nature of the sine function, repeating every \( 2\pi \) radians. Each quadrant of the unit circle gives a quarter of the wave. This visualization helps in comprehending the behavior of sine across different angles.
The graph of cosine
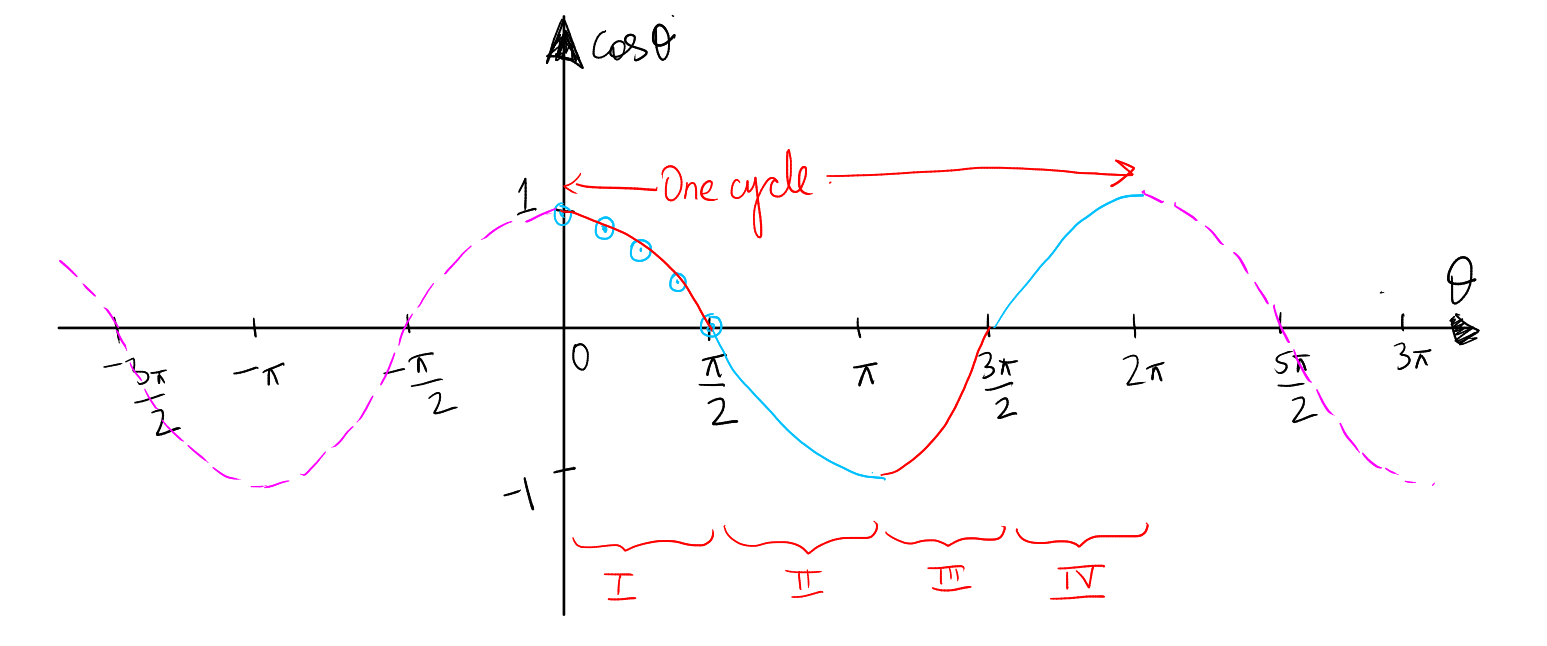
Similar to the graph of sine, we draw the graph of cosine. This time since we know that cosine of \(theta\) is defined to be the abscissa of point \(P\), we focus on \(x\) as \(P\) moves in anticlockwise direction starting from \(A\). With the similar process that we used above we draw the graph of cosine. You may use the following table:
| \( \theta \) | \( \cos(\theta) \) | Ordered Pair \( (\theta, \cos(\theta)) \) |
|---|---|---|
| 0 | 1 | \( (0, 1) \) |
| \( \frac{\pi}{6} \) | \( \frac{\sqrt{3}}{2} \) | \( (\frac{\pi}{6}, \frac{\sqrt{3}}{2}) \) |
| \( \frac{\pi}{4} \) | \( \frac{\sqrt{2}}{2} \) | \( (\frac{\pi}{4}, \frac{\sqrt{2}}{2}) \) |
| \( \frac{\pi}{3} \) | \( \frac{1}{2} \) | \( (\frac{\pi}{3}, \frac{1}{2}) \) |
| \( \frac{\pi}{2} \) | 0 | \( (\frac{\pi}{2}, 0) \) |
Graph of Sine and Cosine superimposed
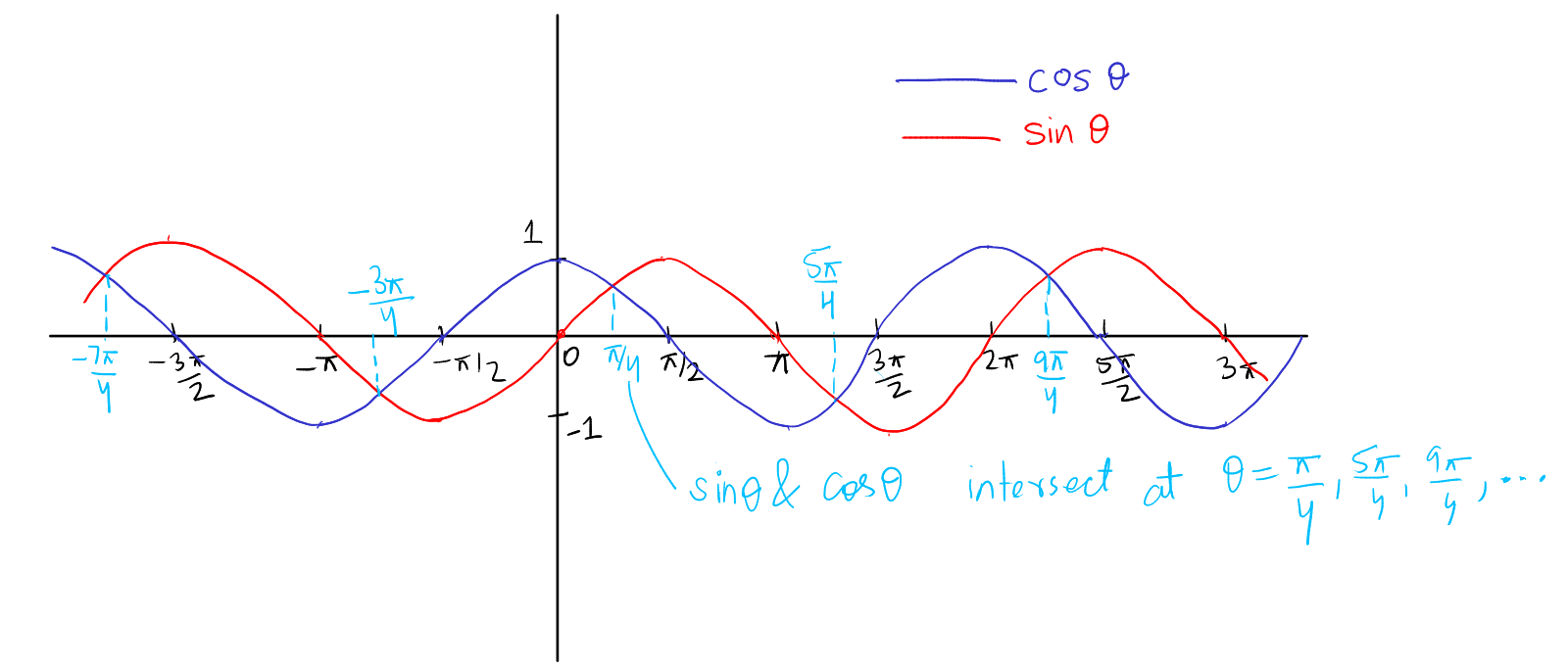
When the graphs of sine and cosine functions are plotted on the same axes, several interesting and fundamental properties of these trigonometric functions become evident.
1. Shape and Symmetry:
- Both sine and cosine graphs have the same shape – a smooth, continuous wave that oscillates between 1 and -1.
- The sine graph starts at the origin (0,0), while the cosine graph starts at its peak (0,1). This difference in starting points is crucial to understanding their relationship.
2. Periodicity:
- Both functions are periodic with a period of \(2\pi\) radians. This means the wave patterns repeat every \(2\pi\) radians along the x-axis.
3. Phase Shift:
- The sine graph can be seen as a shifted version of the cosine graph, or vice versa. Specifically, the sine graph is a horizontal shift of the cosine graph by \( \frac{\pi}{2} \) to the right. In other words, \( \sin(\theta) = \cos(\theta - \frac{\pi}{2}) \). This represents a phase shift between the two functions.
4. Points of Intersection:
- The sine and cosine graphs intersect at points where their values are equal. This occurs at \( \theta = \frac{\pi}{4} \) and \( \theta = \frac{5\pi}{4} \) within the first \(2\pi\) interval. At these points, both sine and cosine have the same value of \( \frac{\sqrt{2}}{2} \) and \( -\frac{\sqrt{2}}{2} \) respectively.
5. Quadrant Analysis:
- In the first quadrant (0 to \( \frac{\pi}{2} \)), both sine and cosine values are positive. In the second quadrant (\( \frac{\pi}{2} \) to \( \pi \)), sine values are positive while cosine values are negative. This pattern continues, reflecting the signs of these functions in each quadrant.
The graph of tan
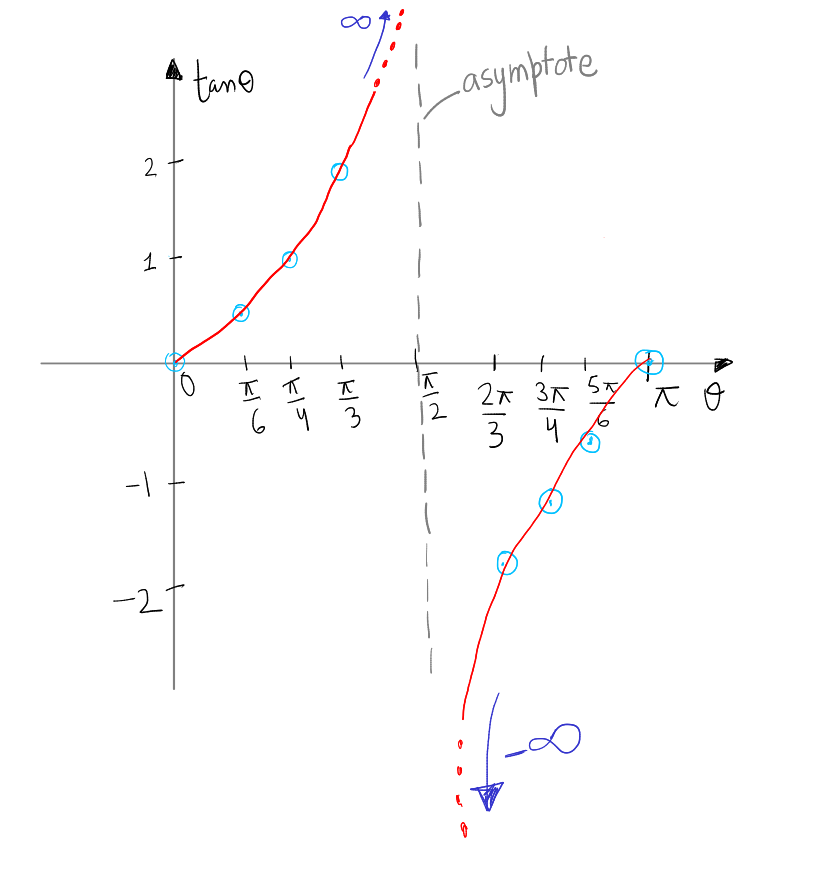
To understand how to draw the graph of tangent, we first analyze the graph in the first quadrant.
The graph of tan in the first quadrant
By definition \(\tan\theta=\frac{y}{x}\), where \((x,y)\) are the coordinates of terminal point \(P\) of angle \(\theta\). as shown in the figure above.
We calibrate the x-axis and y-axis like we did in the grpahs of sine and cosine. We can use the following table to obtain few points on the graph.
| \( \theta \) | \( \tan(\theta) \) | Ordered Pair \( (\theta, \tan(\theta)) \) |
|---|---|---|
| 0 | 0 | \( (0, 0) \) |
| \( \frac{\pi}{6} \) | \( \frac{1}{\sqrt{3}} \) or \( \frac{\sqrt{3}}{3} \) | \( (\frac{\pi}{6}, \frac{\sqrt{3}}{3}) \) |
| \( \frac{\pi}{4} \) | 1 | \( (\frac{\pi}{4}, 1) \) |
| \( \frac{\pi}{3} \) | \( \sqrt{3} \) | \( (\frac{\pi}{3}, \sqrt{3}) \) |
Exploring the Tangent Function as It Nears \( \frac{\pi}{2} \)
\( \tan(\theta) \) shows some interesting behavior near \( \theta = \frac{\pi}{2} \) (or 90 degrees). We say that \( \tan(\theta) \) is 'undefined' at \( \frac{\pi}{2} \). This is because, at this angle on the unit circle, the \( x \)-coordinate of the point is zero, and since tangent is the division \(y\) by \(x\), it's like dividing by zero, which we can't do.
However, what happens when \( \theta \) is very close to \( \frac{\pi}{2} \), but not quite there, is quite interesting. For angles just a little bit less than 90 degrees, like 89 degrees, 89.9 degrees, or even closer, the tangent function is still something we can calculate. But, as \( \theta \) gets closer to 90 degrees, the value of \( \tan(\theta) \) becomes very, very large.
Here's a simple table to show how big the tangent function gets as the angle \( \theta \) gets closer to 90 degrees:
| Angle \( \theta \) (Degrees) | Tangent Value \( \tan(\theta) \) |
|---|---|
| 85 | 11.43 |
| 89 | 57.29 |
| 89.9 | 572.96 |
| 89.99 | 5729.58 |
| 89.999 | 57295.78 |
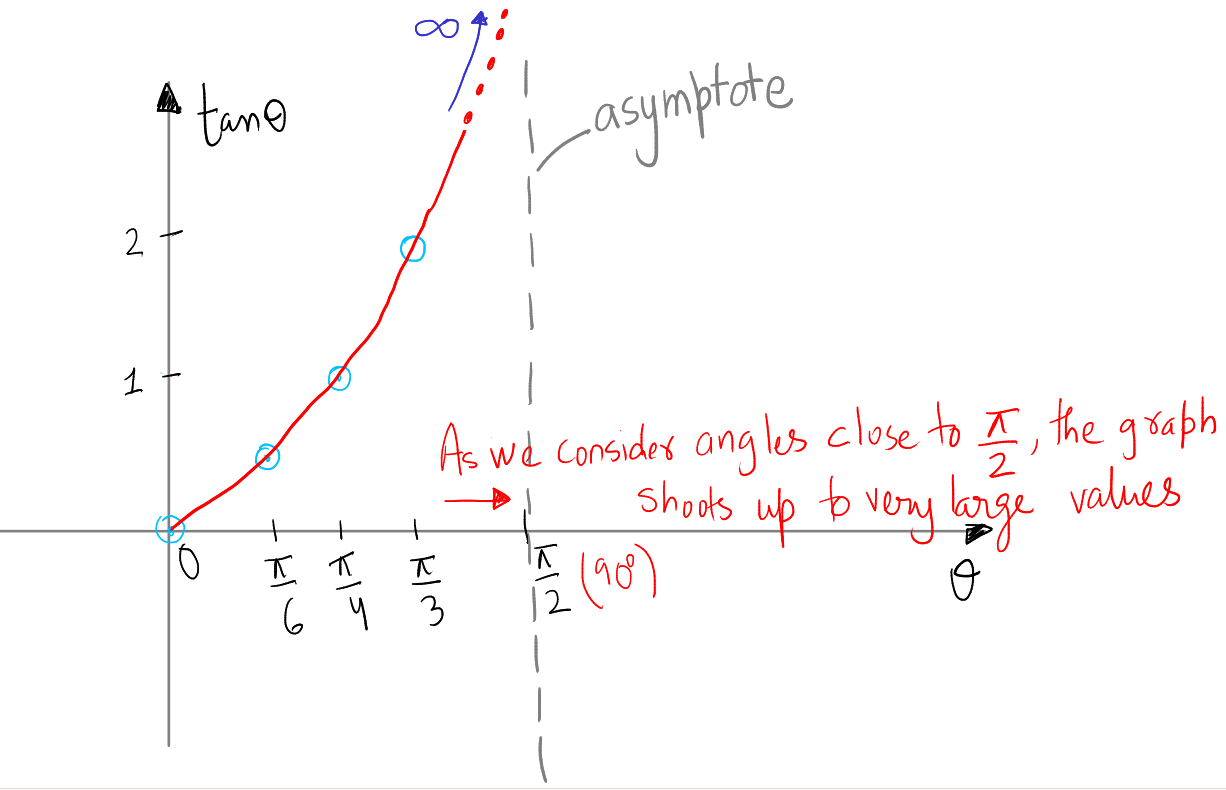When we consider angles \( \theta \) that are less than \( \frac{\pi}{2} \) but increasingly close to it, the behavior of the tangent function, \( \tan(\theta) \), the \( x \)-coordinate of the point on the unit circle corresponding to \( \theta \) approaches zero, while the \( y \)-coordinate approaches 1. As a result, the tangent function, which is the ratio of \( y \) over \( x \) (or \( \sin(\theta) \) over \( \cos(\theta) \)), starts to approach positive infinity. This means that \( \tan(\theta) \) becomes larger and larger as \( \theta \) gets closer to \( \frac{\pi}{2} \). The closer \( \theta \) is to 90 degrees, the closer \( x \) is to zero, and the higher the value of \( \tan(\theta) \) becomes, illustrating a fundamental characteristic of the tangent function near its undefined point at \( \frac{\pi}{2} \).
The graph of tan in second quadrant
To get an idea of how the graph might look like, let us plot some points in the second quadrant. We choose \(theta=\pi, \frac{5\pi}{6}, \frac{3\pi}{4}, \frac{2\pi}{3}\).
| \( \theta \) | \( \tan(\theta) \) | Ordered Pair \( (\theta, \tan(\theta)) \) |
|---|---|---|
| \( \pi \) | 0 | \( (\pi, 0) \) |
| \( \frac{5\pi}{6} \) | \( -\frac{1}{\sqrt{3}} \) or \( -\frac{\sqrt{3}}{3} \) | \( (\frac{5\pi}{6}, -\frac{1}{\sqrt{3}}) \) or \( (\frac{5\pi}{6}, -\frac{\sqrt{3}}{3}) \) |
| \( \frac{3\pi}{4} \) | -1 | \( (\frac{3\pi}{4}, -1) \) |
| \( \frac{2\pi}{3} \) | \( -\sqrt{3} \) | \( (\frac{2\pi}{3}, -\sqrt{3}) \) |
Obviously \(tan\theta\) is negative in the second quadrant. When we approach \(\frac{pi}{2}\)(\(=90^\circ\)), like before the graph shoots down to negative infinity. The reason to which should be apparent by now. If not then, observe the following table:
| \( \theta \) (Degrees) | \( \tan(\theta) \) (Approximate Value) |
|---|---|
| 95 | -11.43 |
| 91 | -57.29 |
| 90.1 | -572.96 |
| 90.01 | -5729.58 |
| 90.001 | -57295.78 |
Which makes the graph looks like this:
The graph of tan in third quadrant
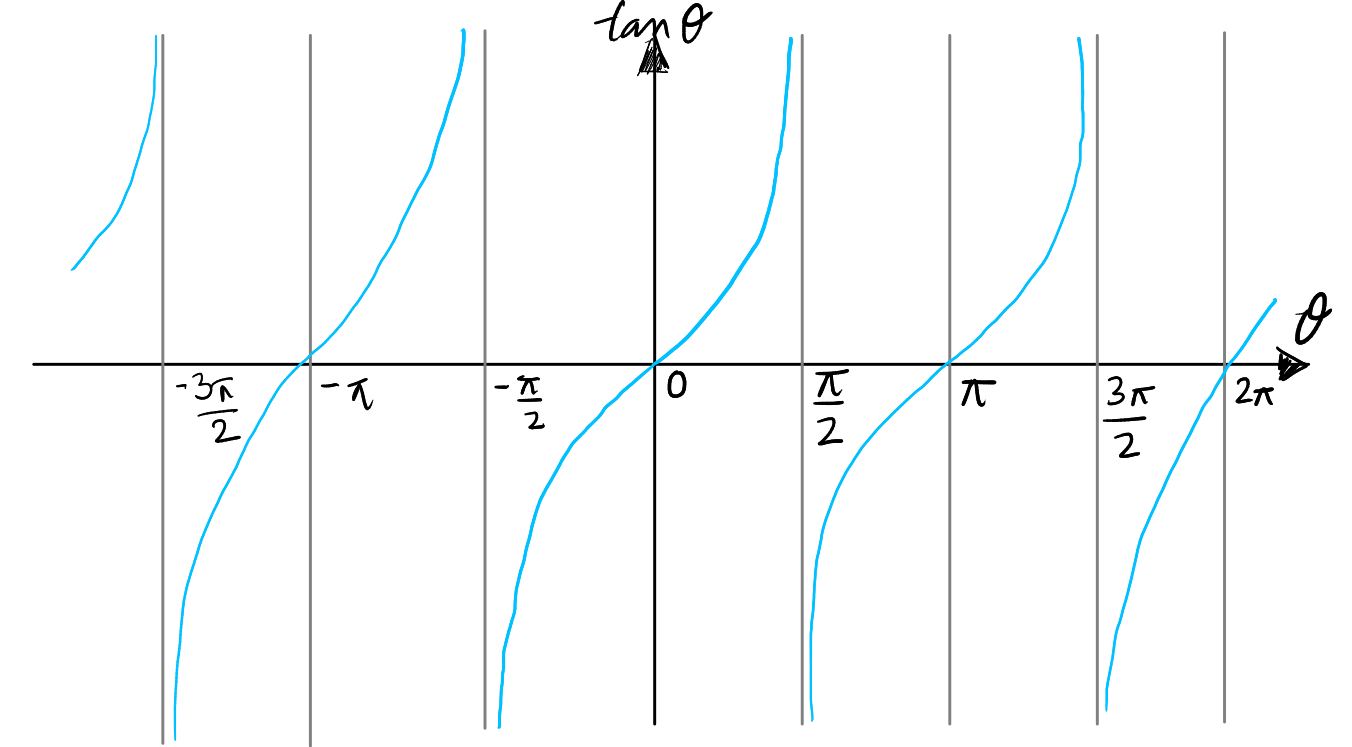
The graph of the tangent function, \( \tan(\theta) \), shows a notable pattern: it is identical in the first and third quadrants. This symmetry arises because of the identity \( \tan(\pi + \theta) = \tan(\theta) \). Simply put, when you add \( \pi \) (180 degrees) to an angle in the first quadrant, you get an angle in the third quadrant with the same tangent value. This relationship results in the tangent function having a period of \( \pi \) radians, and its graph repeats every 180 degrees. So, the portion of the \( \tan(\theta) \) graph from 0 to \( \frac{\pi}{2} \) (first quadrant) is mirrored in the \( \pi \) to \( \frac{3\pi}{2} \) range (third quadrant).
Similarly, the graph in the fourth quadrant is exactly the same as the graph in second quadrant. Interestingly the graph of tan repeats itself every \(\pi\) units. Finally, we get the follwoing graph which we must remember.
Domain of the Tangent Function: The domain of the tangent function, which is the set of all possible input values (angles in this case), includes all real numbers except for the points where the function is undefined. From the graph, it's clear that the tangent function is undefined at \( \frac{\pi}{2} \), \( \frac{3\pi}{2} \), and every odd multiple of \( \frac{\pi}{2} \) (e.g., \( \frac{5\pi}{2} \), \( \frac{7\pi}{2} \), etc.), where the graph shows vertical asymptotes. Therefore, the domain of \( \tan(\theta) \) can be expressed as all real numbers \( \theta \) such that \( \theta \neq \frac{(2n+1)\pi}{2} \), where \( n \) is an integer.
Range of the Tangent Function: The range of the tangent function is the set of all possible output values (tangent of the angle). From the graph, we can observe that as the function approaches its undefined points, the values of \( \tan(\theta) \) increase or decrease without bound. This means that the range of the tangent function is all real numbers, which can be expressed as \( (-\infty, \infty) \).
This graph is an excellent visualization of the periodic and unbounded nature of the tangent function.
Asymtote
An asymptote is a line that a graph gets closer and closer to, but never actually touches or crosses. In simple terms, it's like a boundary that the graph approaches infinitely but never actually reaches or crosses over.
Looking at the graph of tan above, those vertical lines at \( \frac{\pi}{2} \), \( \frac{3\pi}{2} \), and so on, are examples of asymptotes. The curve of the tangent function swoops down or shoots up towards these lines as the angle gets closer to these points, but no matter how close the curve gets, it never actually touches the line. It's as if the curve is trying to reach the line but keeps on going up or down forever, getting closer and closer but never actually making contact.
The graph of cosec
The graph of \( \csc(\theta) \) can be easily constructed from the graph of \( \sin(\theta) \) since \( \csc(\theta) = \frac{1}{\sin(\theta)} \). Here's is the process of drwing the graph of \( \csc(\theta) \):
-
Start with the Sine Graph: Begin by plotting the graph of \( \sin(\theta) \), which oscillates between -1 and 1 and crosses the horizontal axis at multiples of \( \pi \) (0, \( \pi \), \( 2\pi \), etc.).
-
Identify Non-Zero Points: Identify the points where \( \sin(\theta) \) is not zero since \( \csc(\theta) \) will be undefined where \( \sin(\theta) = 0 \).
-
Take Reciprocals: For each non-zero value of \( \sin(\theta) \), find the reciprocal to get the value of \( \csc(\theta) \). For example, when \( \sin(\theta) = 1 \) at \( \theta = \frac{\pi}{2} \), the reciprocal is also 1, so \( \csc(\frac{\pi}{2}) = 1 \).
-
Plot Reciprocal Values: For values of \( \sin(\theta) \) that are greater than 0 but less than 1, their reciprocals will be greater than 1. Plot these on the graph above the horizontal axis.
-
Handle Values Less Than 1: For values of \( \sin(\theta) \) that are negative and greater than -1, their reciprocals will be less than -1. Plot these on the graph below the horizontal axis.
-
Approaching Zero: As \( \sin(\theta) \) approaches zero (as \( \theta \) approaches multiples of \( \pi \)), the reciprocal will grow without bound, meaning \( \csc(\theta) \) will tend towards positive or negative infinity.
-
Draw Asymptotes: Draw vertical lines (asymptotes) at the points where \( \sin(\theta) = 0 \) (multiples of \( \pi \)) since \( \csc(\theta) \) will be undefined at these points.
-
Mirror Sine's Behavior: Remember that \( \csc(\theta) \) will mirror the behavior of \( \sin(\theta) \), but with the values flipped and stretched as you're taking the reciprocal.
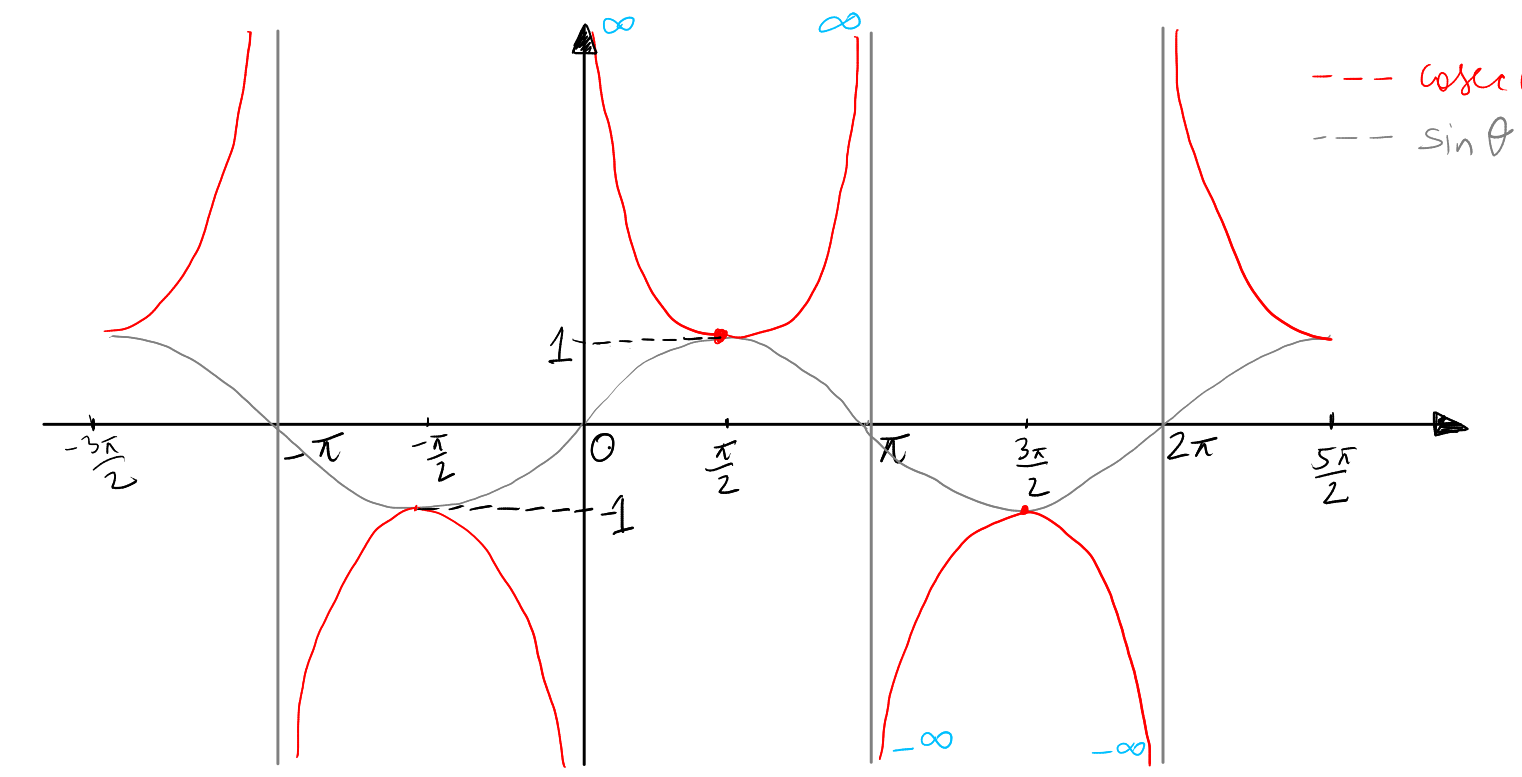
By following these steps, you can draw the graph of \( \csc(\theta) \) which will look like a series of arches that become steeper and narrower as they approach the vertical lines drawn at multiples of \( \pi \), reflecting the reciprocal nature of the cosecant function in relation to sine. Here is the completed graph:
From this graph of the cosecant function (\( \csc(\theta) \)), we can observe:
Domain of \( \csc(\theta) \): The domain of \( \csc(\theta) \) includes all real numbers except where \( \sin(\theta) \) is zero since \( \csc(\theta) = \frac{1}{\sin(\theta)} \). On the graph, \( \sin(\theta) \) is zero at integer multiples of \( \pi \) (e.g., \( 0, \pm\pi, \pm2\pi, \pm3\pi, ... \)). Therefore, these points are not included in the domain of the cosecant function. As a result, the domain of \( \csc(\theta) \) is \( \theta \in \mathbb{R} \setminus \{n\pi \mid n \in \mathbb{Z}\} \).
Range of \( \csc(\theta) \): The range of \( \csc(\theta) \) is all real numbers except between -1 and 1. This is because the cosecant function is the reciprocal of the sine function, and the sine function only takes on values between -1 and 1. Therefore, \( \csc(\theta) \) will never take on values between -1 and 1 since there is no real number whose reciprocal falls within this interval. As seen on the graph, the function approaches positive and negative infinity as it nears points where \( \sin(\theta) = 0 \). Hence, the range is \( \csc(\theta) \in (-\infty, -1] \cup [1, \infty) \).
The graph of secant
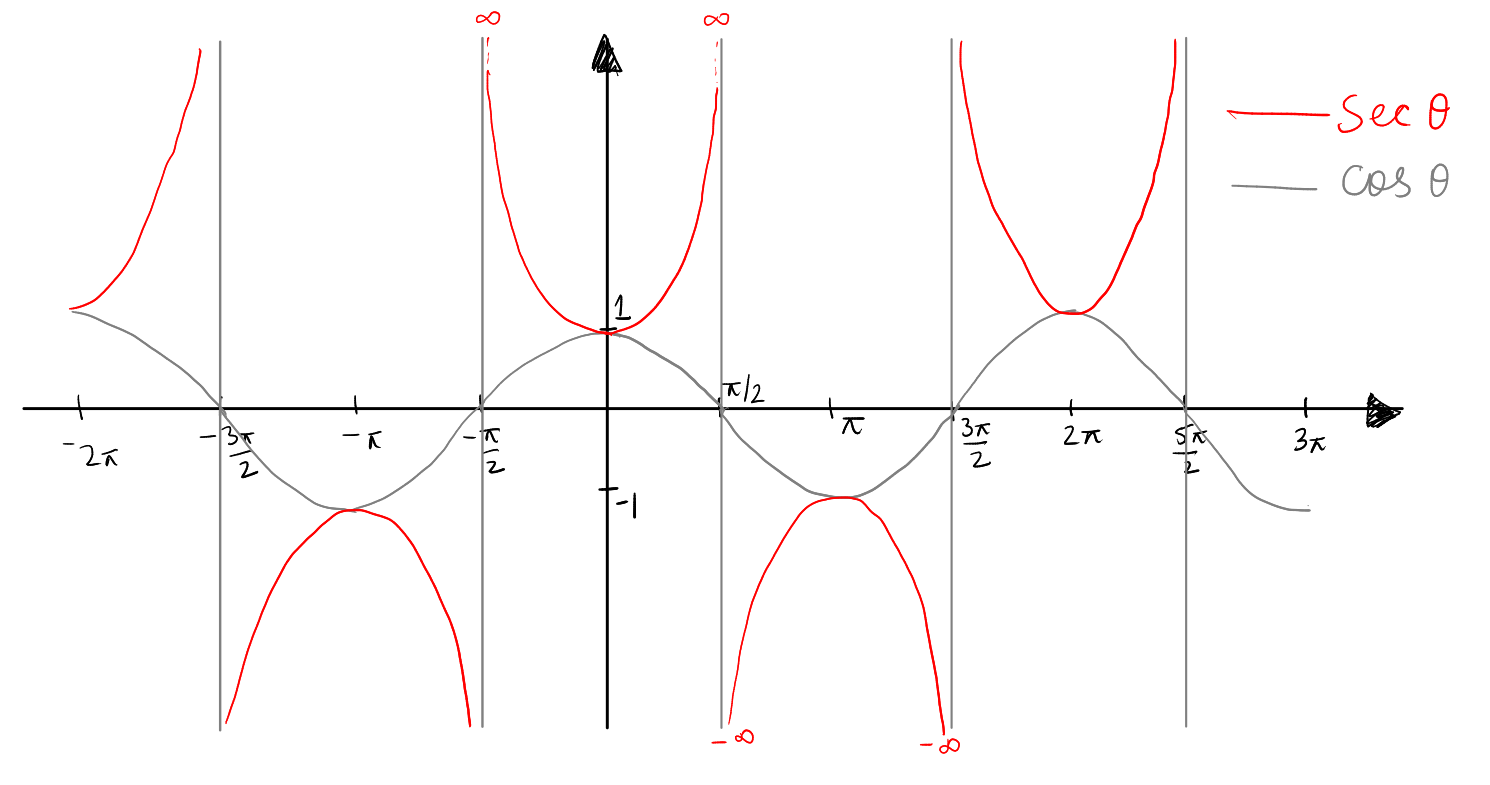
To draw the graph of \( \sec(\theta) \), which is the reciprocal of \( \cos(\theta) \), start by plotting the cosine graph that oscillates between -1 and 1. Wherever the cosine graph has a value, take the reciprocal to get the secant value. For example, when \( \cos(\theta) = 1 \), \( \sec(\theta) \) will also be 1. For values of \( \cos(\theta) \) between 0 and 1, the graph of \( \sec(\theta) \) will be above the horizontal axis and greater than 1. When \( \cos(\theta) \) is negative but greater than -1, the secant graph will be below the horizontal axis and less than -1. As \( \cos(\theta) \) approaches zero, \( \sec(\theta) \) heads off towards positive or negative infinity, which means you'll draw vertical lines (asymptotes) at the points where \( \cos(\theta) = 0 \), such as \( \frac{\pi}{2} \), \( \frac{3\pi}{2} \), etc. The graph of \( \sec(\theta) \) will form a series of U-shaped curves above and inverted U-shapes below these asymptotes, corresponding to where the cosine graph is positive and negative, respectively.
Domain of \( \sec(\theta) \): The secant function is undefined where the cosine function is zero because taking the reciprocal of zero would be undefined. The graph shows that the cosine function equals zero at odd multiples of \( \frac{\pi}{2} \) (e.g., \( \pm\frac{\pi}{2}, \pm\frac{3\pi}{2}, \ldots \)). These points are represented on the graph by vertical asymptotes, indicating that \( \sec(\theta) \) approaches infinity as \( \cos(\theta) \) approaches zero. Therefore, the domain of \( \sec(\theta) \) excludes these points and is \( \theta \in \mathbb{R} \setminus \left\{ \frac{(2k+1)\pi}{2} \mid k \in \mathbb{Z} \right\} \).
Range of \( \sec(\theta) \): The secant function can take any real number except for the interval (-1, 1). As seen in the graph, \( \sec(\theta) \) has a range of \( (-\infty, -1] \cup [1, \infty) \) because \( \sec(\theta) \) approaches negative or positive infinity as the cosine approaches zero and equals ±1 when the cosine equals ±1.
The graph of cot
To draw the graph of the cotangent function, \( \cot(\theta) \), which is the reciprocal of the tangent function, \( \tan(\theta) \), you would follow these steps:
-
Sketch the Tangent Graph: Start by plotting the graph of \( \tan(\theta) \), which has a period of \( \pi \), with vertical asymptotes at every \( \theta = \frac{\pi}{2} + n\pi \) for integers \( n \).
-
Identify Non-Zero Points: Determine the points on the tangent graph that are not zero, as \( \cot(\theta) \) will be undefined at \( \theta \) where \( \tan(\theta) = 0 \).
-
Take Reciprocals: For each point on the \( \tan(\theta) \) graph that is not zero, calculate the reciprocal to find the corresponding \( \cot(\theta) \) value.
-
Plot Reciprocal Values: Where \( \tan(\theta) \) is positive, \( \cot(\theta) \) will be positive and vice versa. As \( \tan(\theta) \) approaches zero from positive, \( \cot(\theta) \) will approach infinity, and where \( \tan(\theta) \) approaches zero from negative, \( \cot(\theta) \) will approach negative infinity.
-
Draw Asymptotes and Curves: The points where \( \tan(\theta) = 0 \) become the asymptotes for the \( \cot(\theta) \) graph. Between the asymptotes, \( \cot(\theta) \) will form a series of decreasing curves in each period, going from positive infinity through zero to negative infinity as \( \theta \) increases from \( n\pi \) to \( \frac{\pi}{2} + n\pi \).
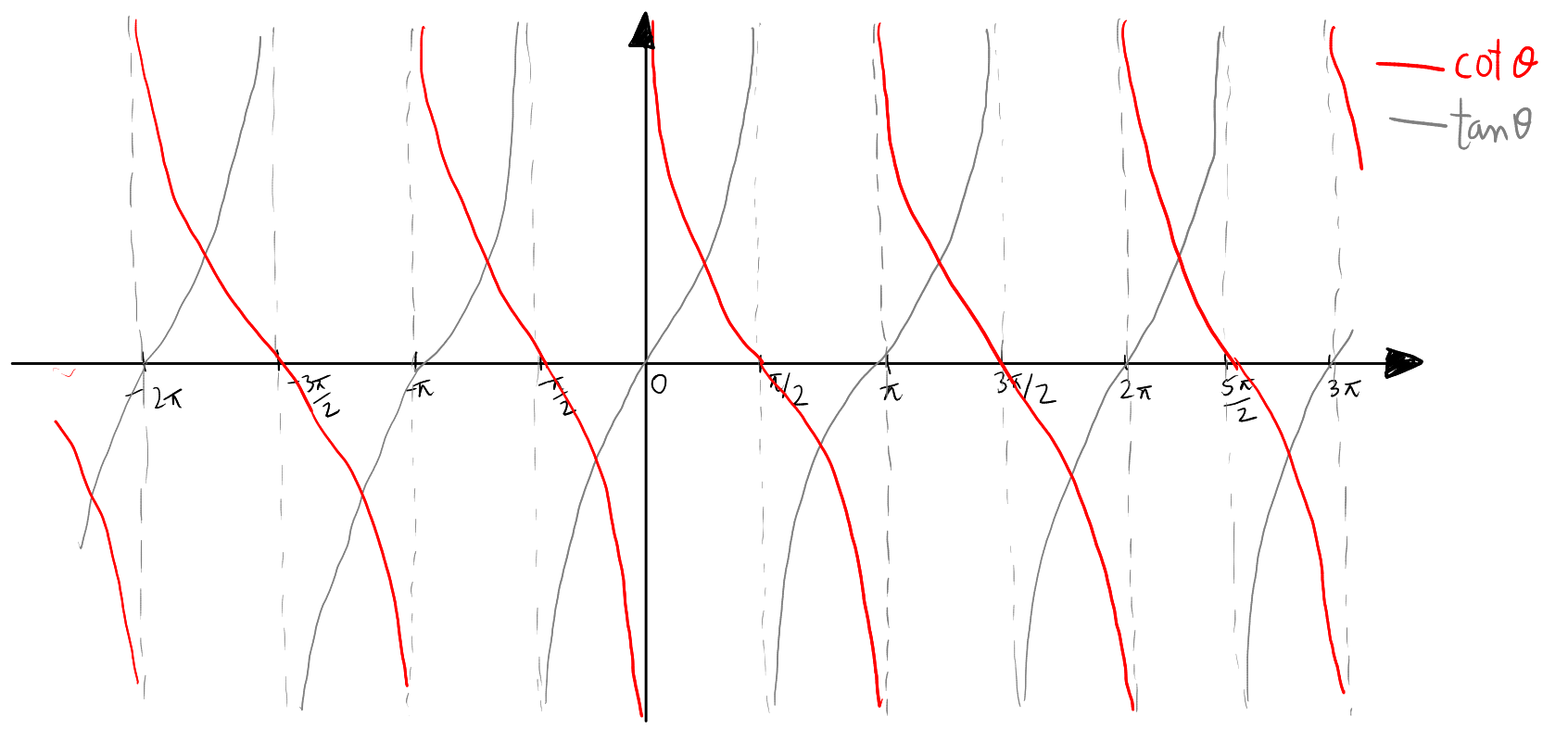
By repeating this process over the range of \( \theta \), you can create the full graph of \( \cot(\theta) \), which will appear as a series of downward-opening curves that approach the vertical asymptotes at multiples of \( \pi \).
Domain of \( \cot(\theta) \): The cotangent function is the reciprocal of the tangent function. The graph shows that \( \cot(\theta) \) is undefined where the tangent function is zero, which occurs at integer multiples of \( \pi \) (e.g., \( 0, \pm\pi, \pm2\pi, \ldots \)). These points are represented on the graph by vertical asymptotes, indicating that the function approaches infinity as it nears these points. Therefore, the domain of \( \cot(\theta) \) excludes these points and is \( \theta \in \mathbb{R} \setminus \{k\pi \mid k \in \mathbb{Z}\} \).
Range of \( \cot(\theta) \): As seen in the graph, \( \cot(\theta) \) takes on all real number values. There are no restrictions on the output values of \( \cot(\theta) \) as it can go from negative to positive infinity. Thus, the range of the cotangent function is all real numbers, which can be written as \( \cot(\theta) \in (-\infty, \infty) \).