More Properties of Real Numbers
Reciprocal Properties
The reciprocal properties of real numbers relate to how the sign and relative magnitude of non-zero numbers affect their reciprocals. Here are the properties clearly outlined:
-
Positive Numbers and Their Reciprocals:
- If \( a > 0 \), then its reciprocal \( \frac{1}{a} > 0 \).
This property states that the reciprocal of a positive number is also positive. Since dividing by a positive number does not change the sign, the reciprocal maintains the positivity.
-
Negative Numbers and Their Reciprocals:
- If \( a < 0 \), then its reciprocal \( \frac{1}{a} < 0 \).
In contrast to positive numbers, the reciprocal of a negative number is also negative. Dividing by a negative number reverses the sign, so the negative sign is preserved when taking the reciprocal.
-
Comparing Positive Numbers and Their Reciprocals:
- If \( a, b > 0 \) and \( a < b \), then \( \frac{1}{a} > \frac{1}{b} \).
When comparing two positive numbers where one is larger than the other, their reciprocals will have the opposite inequality. This "reversal" happens because, as \( a \) grows larger, \( \frac{1}{a} \) becomes smaller.
-
Comparing Negative Numbers and Their Reciprocals:
- If \( a, b < 0 \) and \( a < b \), then \( \frac{1}{a} > \frac{1}{b} \).
Similarly, when comparing two negative numbers, the one that is more negative (or smaller in absolute value) will have a larger reciprocal. This is also a reversal of the inequality and follows from the fact that for negative numbers, as the absolute value increases, the reciprocal decreases.
These reciprocal properties are fundamental in understanding the behavior of real numbers under division, especially when dealing with inequalities, and they are particularly useful in algebraic manipulations and solving equations.
We can apply these properties to prove the following important results:
-
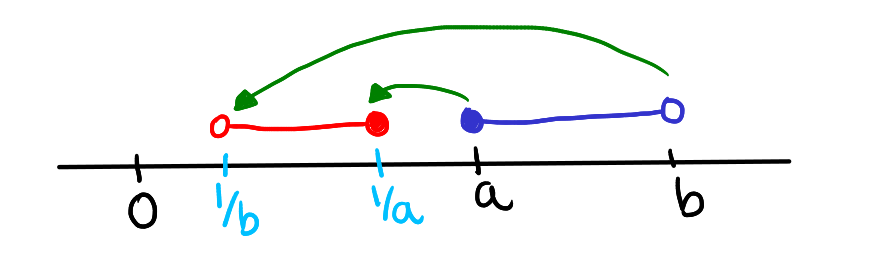
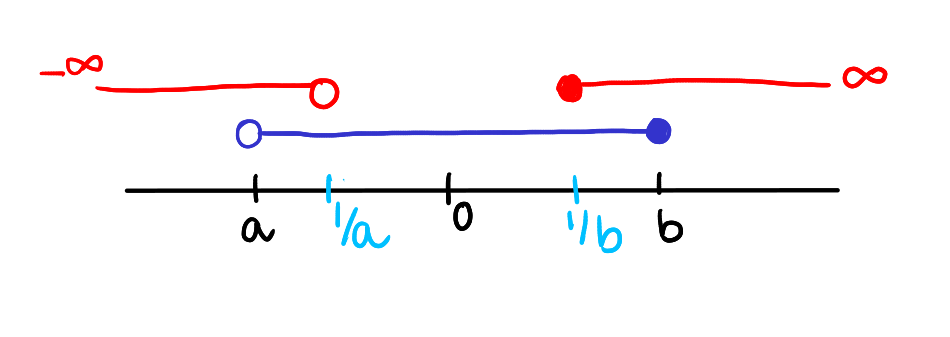
If \( a > 0 \) and \( b > 0 \), then for \( x \) such that \( a \leq x < b \), the reciprocal \( \frac{1}{x} \) will satisfy \( \frac{1}{b} < \frac{1}{x} \leq \frac{1}{a} \).
We can also state the ibove in the interval form as: for \( x \) in the interval \( [a, b) \), the reciprocal \( \frac{1}{x} \) will be in the interval \( (1/b, 1/a] \).
Proof:
- From the inequality \( a \leq x \), where \( a > 0 \), by taking the reciprocal of each side, we get \( \frac{1}{a} \geq \frac{1}{x} \).
-
From the inequality \( x < b \), where \( b > 0 \) and \(x\> 0 \), taking reciprocals reverses the inequality to \( \frac{1}{x} > \frac{1}{b} \).
-
Combining these results, for \( x \) within the interval \( [a, b) \), the reciprocal \( \frac{1}{x} \) must lie within \( (1/b, 1/a] \).
-
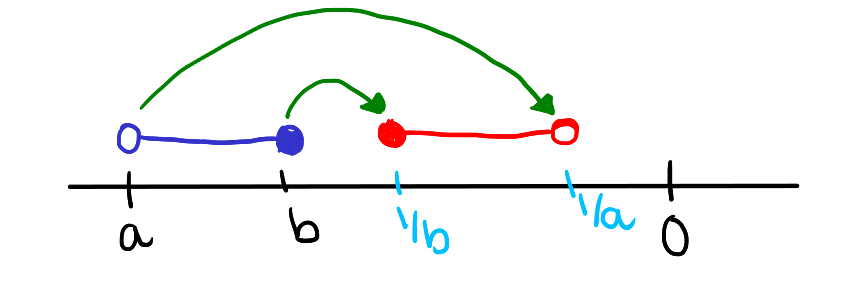
If \( a < 0 \) and \( b < 0 \), then for \( x \) such that \( a < x \leq b \), the reciprocal \( \frac{1}{x} \) will satisfy \( \frac{1}{b} \leq \frac{1}{x} < \frac{1}{a} \).
In interval form: for \( x \) in the interval \( (a, b] \), the reciprocal \( \frac{1}{x} \) will be in the interval \( [1/b, 1/a) \).
Proof:
-
Starting with \( a < x \), and knowing that both \( a \) and \( x \) are negative, the reciprocal of each side yields \( \frac{1}{a} > \frac{1}{x} \) because reciprocating two negative numbers reverses the inequality sign, and the larger the negative number, the smaller its reciprocal in magnitude.
-
Similarly, from \( x \leq b \), where both \( b \) and \( x \) are negative, the reciprocal of each side results in \( \frac{1}{x} \geq \frac{1}{b} \), as a smaller or equal negative number leads to a larger or equal reciprocal.
-
When these reciprocal inequalities are combined, they imply that for \( x \) in the interval \( (a, b] \), \( \frac{1}{x} \) must fall within the interval \( [1/b, 1/a) \). Here, \( \frac{1}{b} \) is included because \( b \) is the upper bound for \( x \) and thus \( \frac{1}{x} \) can equal \( \frac{1}{b} \), while \( \frac{1}{a} \) is excluded because \( a \) is the lower bound for \( x \) and \( \frac{1}{x} \) cannot equal \( \frac{1}{a} \), as that would require \( x \) to be \( a \), which is outside the given interval for \( x \).
-
-
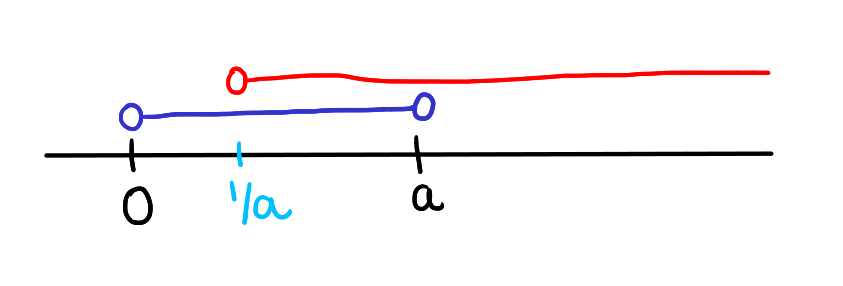
If \( a > 0 \), then for \( x \) such that \( 0 < x < a \), the reciprocal \( \frac{1}{x} \) satisfies \( \frac{1}{a} < \frac{1}{x} \).
In interval form, for \( x \) in the interval \( (0, a) \), the reciprocal \( \frac{1}{x} \) falls within the interval \( \left(\frac{1}{a}, \infty\right) \).
Proof:
-
Comparing \( x \) and \( a \):
- Since \( x \) is positive and less than \( a \) (also positive), the reciprocal of \( x \) will be larger than the reciprocal of \( a \). This happens because dividing one by a smaller number gives a larger result.
-
Effect of \( x \) Approaching 0:
- As \( x \) gets closer to zero but remains positive, \( \frac{1}{x} \) starts to increase, moving towards a very large number. In fact, as \( x \) approaches zero, \( \frac{1}{x} \) keeps increasing and can become as large as we can imagine.
Within the interval \( (0, a) \), as \( x \) gets smaller, \( \frac{1}{x} \) becomes larger. Starting from \( \frac{1}{a} \), \( \frac{1}{x} \) moves beyond this value and continues to increase indefinitely as \( x \) approaches zero. Thus, the values of \( \frac{1}{x} \) will be within \( (\frac{1}{a}, \infty) \), demonstrating that the smaller \( x \) gets within this interval, the larger \( \frac{1}{x} \) becomes.
Converse
The converse statement is:
If \( a > 0 \), then for \( x \) such that \( x > a \), the reciprocal \( \frac{1}{x} \) satisfies \( 0 < \frac{1}{x} < \frac{1}{a} \).
In interval form, for \( x \) in the interval \( (a, \infty) \), the reciprocal \( \frac{1}{x} \) falls within the interval \( (0, \frac{1}{a}) \).
-
-
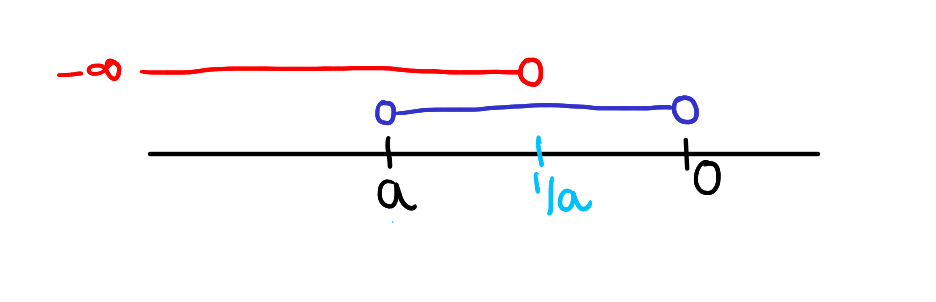
If \( a < 0 \), then for \( x \) such that \( a < x < 0 \), the reciprocal \( \frac{1}{x} \) satisfies \( -\infty < \frac{1}{x} < \frac{1}{a} \). That is, if \( a < 0 \), and \( x \) is in the interval \( (a, 0) \), then the reciprocal \( \frac{1}{x} \) will be in the interval \( (-\infty, \frac{1}{a}) \).
Proof:
-
Relative Position and Reciprocation:
- Since both \( a \) and \( x \) are negative with \( a < x \), \( x \) is closer to zero. The reciprocity rule states that for two negative numbers, the one closer to zero has the greater reciprocal. Therefore, \( \frac{1}{x} < \frac{1}{a} \).
-
Limits as \( x \) Approaches Zero:
- As \( x \) approaches zero from the left (increasing in value but remaining negative), \( \frac{1}{x} \) grows and heads towards positive infinity, following the property that the reciprocal of a negative number close to zero trends towards large positive values.
Converse
The converse for the given statement is:
If \( a < 0 \), then for \( x \) such that \( x < a \), it follows that \( \frac{1}{a} < \frac{1}{x} <0 \).
Expressed using interval notation as:
\[ x \in (-\infty, a) \implies \frac{1}{x} \in (\frac{1}{a}, 0) \] -
-
If \( a < 0 \) and \( b > 0 \), then for \( x \) such that \( a < x \leq b \), the reciprocal \( \frac{1}{x} \) satisfies either \( -\infty < \frac{1}{x} < \frac{1}{a} \) or \( \frac{1}{b} \leq \frac{1}{x} < \infty \). That is, for \( x \) in the interval \( (a, b] \), the reciprocal \( \frac{1}{x} \) will be in the intervals \( (-\infty, \frac{1}{a}) \cup [\frac{1}{b}, \infty) \).
Proof:
Divide \((a,b]\) into two parts \((a, 0)\) and \((0, b]\). We utilize previous reciprocal theorems concerning positive and negative intervals and apply them to the divided segments of \( (a, b] \): \( (a, 0) \) for negative \( x \) and \( (0, b] \) for positive \( x \).
-
For Interval \( (a, 0) \):
- Applying the theorem for negative values, since \( a < x < 0 \), the reciprocal \( \frac{1}{x} \) falls in \( (-\infty, \frac{1}{a}) \).
-
For Interval \( (0, b] \):
- Utilizing the theorem for positive values, with \( 0 < x \leq b \), the reciprocal \( \frac{1}{x} \) spans \( [\frac{1}{b}, \infty) \).
Combining the findings from both segments, the overall reciprocal interval for \( x \) in \( (a, b] \) is the union of \( (-\infty, \frac{1}{a}) \) and \( [\frac{1}{b}, \infty) \). Therefore, for \( x \) within \( (a, b] \), \( \frac{1}{x} \) lies within \( (-\infty, \frac{1}{a}) \cup [\frac{1}{b}, \infty) \). This conclusion is drawn directly from the previously established properties of reciprocals for positive and negative real numbers.
-
Summary
-
For \( a > 0, b > 0 \), and \( a \leq x < b \):
\[x \in [a, b) \implies \frac{1}{x} \in (1/b, 1/a]\] -
For \( a < 0, b < 0 \), and \( a < x \leq b \):
\[x \in (a, b] \implies \frac{1}{x} \in [1/b, 1/a)\] -
For \( a > 0 \), and \( 0 < x < a \):
\[x \in (0, a) \implies \frac{1}{x} \in (\frac{1}{a}, \infty)\] -
For \( a < 0 \), and \( a < x < 0 \):
\[x \in (a, 0) \implies \frac{1}{x} \in (-\infty, \frac{1}{a})\] -
For \( a < 0, b > 0 \), and \( a < x \leq b \):
\[x \in (a, b] \implies \frac{1}{x} \in (-\infty, \frac{1}{a}) \cup [\frac{1}{b}, \infty)\]
Example
Solve the inequality \(\frac{x}{1-x} > 3\).
-
Rewrite the Inequality:
Start by expressing the given inequality within an extended range:
\[ 3 < \frac{x}{1-x} < \infty \] -
Take the Reciprocal:
Taking the reciprocal of each part reverses the inequality:
\[ 0 < \frac{1-x}{x} < \frac{1}{3} \] -
Simplify the Reciprocal Expression:
Break down and rearrange the middle part of the inequality:
\[ 0 < \frac{1}{x} - 1 < \frac{1}{3} \] -
Isolate \(\frac{1}{x}\):
Adjust the inequality to isolate \(\frac{1}{x}\):
\[ 1 < \frac{1}{x} < \frac{4}{3} \] -
Take the Reciprocal Again:
Taking the reciprocal again (and reversing the inequality signs):
\[ \frac{3}{4} < x < 1 \]The solution to the inequality \(\frac{x}{1-x} > 3\) is:
\[ x \in \left(\frac{3}{4}, 1\right) \]This interval represents the values of \(x\) for which the original inequality holds true.
-
Rewrite the Inequality with a Common Denominator:
Start by subtracting 3 from both sides of the inequality and placing the terms under a common denominator:
\[ \frac{x}{1-x} - 3 > 0 \implies \frac{x - 3(1-x)}{1-x} > 0 \] -
Simplify the Numerator:
Distribute and combine like terms in the numerator:
\[ \frac{x - 3 + 3x}{1-x} > 0 \implies \frac{4x - 3}{1-x} > 0 \implies \frac{4x - 3}{x-1} < 0 \] -
Draw a Wavy Curve:
Using the wavy curve method, we get \(x \in \left(\frac{3}{4}, 1\right)\)
Squaring
-
Given \( a > 0 \), \( b > 0 \), if \( a < b \) then \( a^2 < b^2 \).
The inequality does not reverse when squaring positive numbers. If one positive number is smaller than another, its square will also be smaller.
Example:
- \( a = 3 \) and \( b = 5 \)
- Therefore, \( 3 < 5 \) implies \( 3^2 = 9 < 5^2 = 25 \).
-
Given \( a < 0 \), \( b < 0 \), if \( a < b \) then \( a^2 > b^2 \).
The inequality reverses when squaring negative numbers. If one negative number is less than another, its square will be greater because the signs cancel out, leaving the absolute values to determine the inequality, which reverses due to the initial negative values.
Example:
- \( a = -5 \) and \( b = -3 \)
- Therefore, \( -5 < -3 \) implies \( (-5)^2 = 25 > (-3)^2 = 9 \).
-
Property 1: \(x^2 < a^2\) implies \(-a < x < a\), or \(x \in (-a, a)\).
Proof:
Starting from the given inequality:
\[ x^2 < a^2 \]This can be rewritten as:
\[ x^2 - a^2 < 0 \]Factoring the difference of squares:
\[ (x - a)(x + a) < 0 \]From this wavy curve, the expression \((x - a)(x + a)\) is negative only in the interval \(x \in (-a, a)\), confirming that:
\[ x^2 < a^2 \implies x \in (-a, a) \]Property 2: \(x^2 \leq a^2\) implies \(-a \leq x \leq a\), or \(x \in [-a, a]\).
Property 3: \(x^2 > a^2\) implies \(x > a\) or \(x < -a\), or \(x \in (-\infty, -a) \cup (a, \infty)\).
Property 4: \(x^2 \geq a^2\) implies \(x \geq a\) or \(x \leq -a\), or \(x \in [-\infty, -a] \cup [a, \infty]\).
Property 5: \(a^2 < x^2 < b^2\) implies \(a < x \leq b\) or \(-b \leq x < -a\), or \(x \in ([-b, -a) \cup (a, b])\).
Proof:
To prove the property that if \(a^2 < x^2 < b^2\) then \(x \in ([-b, -a) \cup (a, b])\), we can break this down into two separate inequalities and analyze the intersection of their solutions:
-
Break Down the Inequality:
Consider the inequality \(a^2 < x^2 < b^2\) as two separate parts:
- \(x^2 > a^2\)
- \(x^2 < b^2\)
-
Solve Each Inequality:
-
For \(x^2 > a^2\):
\[ x \in (-\infty, -a) \cup (a, \infty) \] -
For \(x^2 < b^2\):
\[ x \in (-b, b) \]
-
-
Intersection of Solutions:
To find the solution to the original compound inequality \(a^2 < x^2 < b^2\), take the intersection of the two intervals derived above:
- The interval \(x \in (-\infty, -a) \cup (a, \infty)\) represents all \(x\) values where the magnitude of \(x\) is greater than \(a\).
- The interval \(x \in (-b, b)\) represents all \(x\) values where the magnitude of \(x\) is less than \(b\).
The intersection of these two sets, considering \(a < b\), is:
\[ x \in ([-b, -a) \cup (a, b]) \]
-
Example
Solve the inequality \((2x-1)^2 > 5\).
Solution:
-
\[ (2x-1)^2 > 5 \implies (2x-1)^2 > (\sqrt(5))^2 \]\[ \implies 2x-1 > \sqrt{5} \quad \text{or} \quad 2x-1 < -\sqrt{5} \]
-
Solve each inequality for \(x\):
-
Solving \(2x - 1 > \sqrt{5}\):
\[ 2x > \sqrt{5} + 1 \]\[ x > \frac{\sqrt{5} + 1}{2} \] -
Solving \(2x - 1 < -\sqrt{5}\):
\[ 2x < -\sqrt{5} + 1 \]\[ x < \frac{-\sqrt{5} + 1}{2} \]
-
The solution to the inequality \((2x-1)^2 > 5\) is: