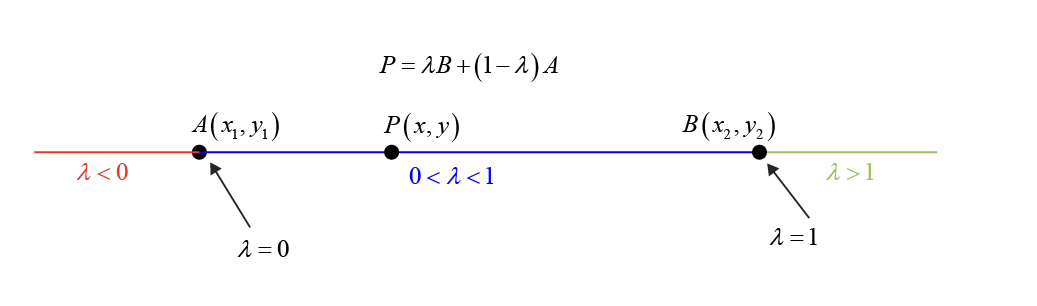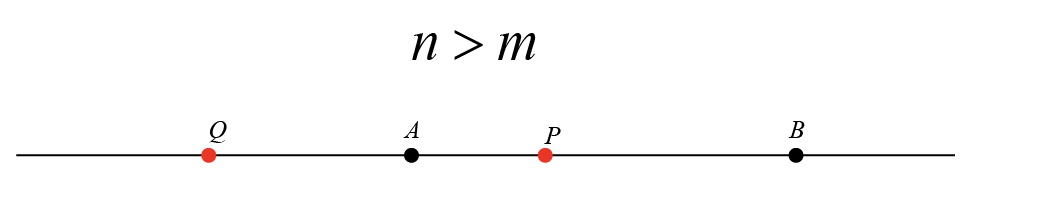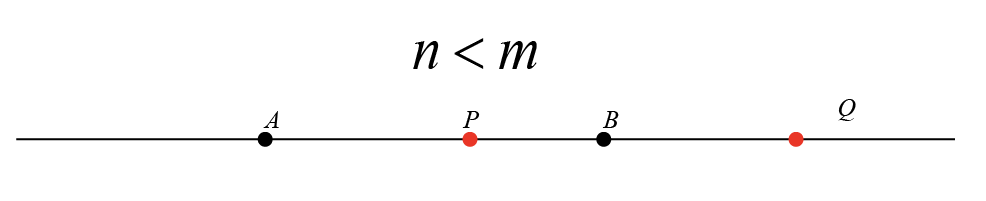Section Formula and Centres of a Triangle

Section Formula

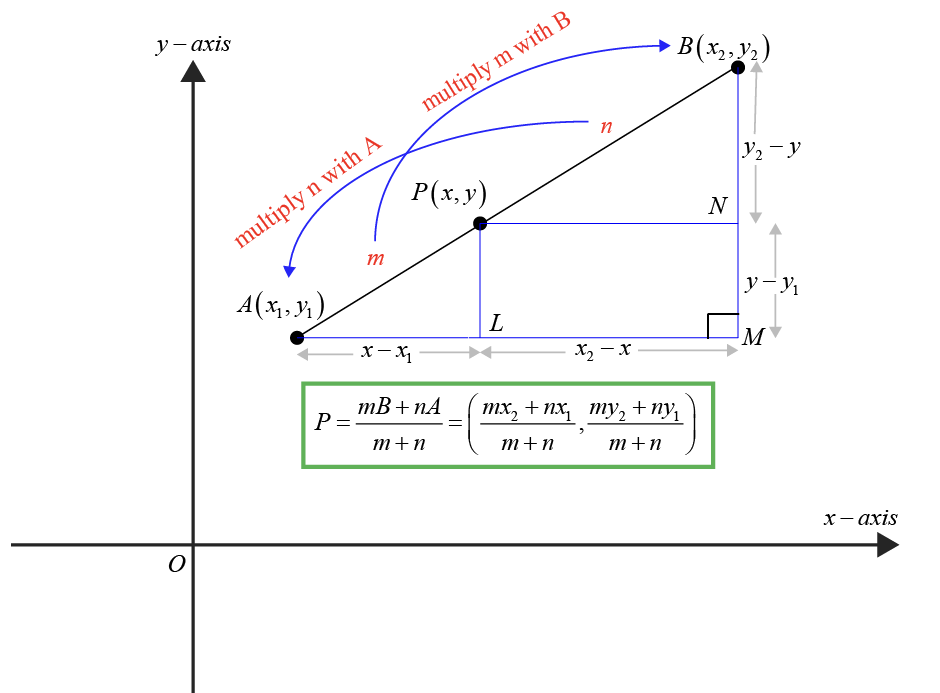
Given points \(A(x_1, y_1)\) and \(B(x_2, y_2)\) and a point \(P(x, y)\) that divides the line segment \(AB\) internally in the ratio \(m:n\), we can derive the coordinates of point \(P\) using the section formula.

Section Formula for Internal Division:

The point \(P\) dividing the line segment \(AB\) internally in the ratio \(m:n\) has coordinates given by

\[ x = \frac{mx_2 + nx_1}{m + n} \]

\[ y = \frac{my_2 + ny_1}{m + n} \]

Proof:

Consider the right-angled triangles \(PNB\) and \(PLA\) as shown in the figure below:

It is straightforward to prove that \(\Delta PNB\sim\Delta PLA\)

From these proportions, we can write:

1. \(\frac{AL}{PN}=\frac{PA}{PB}\)

   \( \implies \frac{x-x_1}{x_2-x}=\frac{m}{n} \)

   \(\implies nx-nx_1=mx_2-mx\)

   \(\implies x=\frac{mx_2+nx_1}{m+n}\)

2. \(\frac{PL}{BN}=\frac{PA}{PB}\)

   \( \implies \frac{y-y_1}{y_2-y}=\frac{m}{n} \)

   \(\implies ny-ny_1=my_2-my\)

   \(\implies y=\frac{my_2+ny_1}{m+n}\)

This concludes the proof of the section formula for internal division of a line segment.

Alternate way to write ratio

In coordinate geometry, when simplifying the algebraic representation of the ratio of division of a line segment, it's common to introduce a parameter \( \lambda \) to represent the ratio \( \frac{m}{n} \). This is particularly useful when dealing with problems involving section formulae, as it allows us to express the coordinates of the dividing point \( P(x, y) \) in a more streamlined form.

Using \( \lambda = \frac{m}{n} \), the section formula for internal division becomes:

\[ x = \frac{\lambda x_2 + x_1}{\lambda + 1} \]

\[ y = \frac{\lambda y_2 + y_1}{\lambda + 1} \]

This is because the original expressions:

\[ x = \frac{mx_2 + nx_1}{m + n} \]

\[ y = \frac{my_2 + ny_1}{m + n} \]

can be rewritten by dividing the numerator and denominator by \( n \) (assuming \( n \neq 0 \)), resulting in:

\[ x = \frac{\frac{m}{n}x_2 + 1 \cdot x_1}{\frac{m}{n} + 1} = \frac{\lambda x_2 + x_1}{\lambda + 1} \]

\[ y = \frac{\frac{m}{n}y_2 + 1 \cdot y_1}{\frac{m}{n} + 1} = \frac{\lambda y_2 + y_1}{\lambda + 1} \]

Hence, the point \( P \) dividing the line segment \( AB \) internally in the ratio \( \lambda:1 \) (or \( m:n \)) has its coordinates given by the simplified section formula above.

Section Formual for External division

The coordinates of a point \( P(x, y) \) that divides the line segment joining two points \( A(x_1, y_1) \) and \( B(x_2, y_2) \) in the ratio \( m:n \) externally are given by \( \left( \frac{mx_2 - nx_1}{m-n}, \frac{my_2 - ny_1}{m-n} \right) \).

Proof: A similar proof as Internal division ensues. Please try to do it yourself.

Unified formula of Internal and external division: Positive and Negative Ratio

For the coordinates of a point \(P\) dividing the line segment \(AB\) externally in the ratio \(m:n\), the formula is given by \((\frac{mx_2 - nx_1}{m-n}, \frac{my_2 - ny_1}{m-n})\). This can also be written as \((\frac{mx_2 + (-n)x_1}{m + (-n)}, \frac{my_2 + (-n)y_1}{m + (-n)})\) by absorbing the negative sign. The ratio for external division can be denoted as \(-m:n\), where the negative sign indicates external division. Thus, for any division ratio \(m:n\), whether positive or negative, the formula \((\frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n})\) can be used.

Alternative way of writing the unified formula

Given the formula for the coordinates of \(P\):

\[P(x, y) = \left( \frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n} \right)\]

Dividing both numerator and denominator by \(n\), we get:

\[P(x, y) = \left( \frac{\frac{m}{n}x_2 + x_1}{\frac{m}{n} + 1}, \frac{\frac{m}{n}y_2 + y_1}{\frac{m}{n} + 1} \right)\]

Substituting \(\lambda = \frac{m}{n}\), we obtain:

\[P(x, y) = \left( \frac{\lambda x_2 + x_1}{\lambda + 1}, \frac{\lambda y_2 + y_1}{\lambda + 1} \right)\]

This formula compactly expresses the coordinates of \(P\) dividing the segment \(AB\) in the ratio \(m:n\) or equivalently \(\lambda:1\), where \(\lambda\) can be any real number, capturing both internal and external division scenarios.

Location of point P depending on lambda

The location of point \(P\), dividing a line segment \(AB\) in the ratio \(\lambda:1\) (where \(\lambda = \frac{m}{n}\)), relative to points \(A\) and \(B\), varies depending on the value of \(\lambda\):

1. \(\lambda = 0\): Point \(P\) coincides with point \(A\). This is because the division ratio effectively becomes \(0:1\), indicating that \(P\) is at \(A\).

2. \(\lambda>0\): Point \(P\) lies between \(A\) and \(B\). As \(\lambda\) changes from \(0\) to \(\infty\), \(P\) moves from \(A\) towards \(B\).

3. \(-1 < \lambda < 0\): Point \(P\) divides \(AB\) externally but is closer to \(A\). In this range, \(\lambda\) is negative, signifying external division, but since \(|\lambda| < 1\), \(P\) is positioned on the extension of \(AB\) on \(A\)'s side.

4. \(\lambda < -1\): Point \(P\) divides \(AB\) externally on the side of \(B\). Here, the absolute value of \(\lambda\) being greater than 1 means that \(P\) not only divides \(AB\) externally but also lies closer to \(B\), on the extension of \(AB\) beyond \(B\).

These scenarios illustrate how the value of \(\lambda\) determines \(P\)'s relative location to \(A\) and \(B\), spanning both internal and external divisions along and beyond the segment \(AB\).

Yet another way of writing the ratio

When the ratio of the lengths of segments \(AP\) to \(AB\) is taken as \(\lambda\), that is, \(AP:AB = \lambda\), a different approach is used to find the coordinates of point \(P\). This implies that \(AP\) is a fraction \(\lambda\) of the total length \(AB\). Consequently, the ratio \(AP:PB\) can be expressed as \(\lambda:(1-\lambda)\), since \(AP + PB = AB\) and \(PB = AB - AP\).

Given this, the coordinates of point \(P\) can be derived from the ratio \(AP:PB = \lambda:(1-\lambda)\) as follows:

\[P(x, y) = \left( \frac{\lambda x_2 + (1-\lambda) x_1}{1}, \frac{\lambda y_2 + (1-\lambda) y_1}{1} \right)\]

This formula simplifies to:

\[\color{green}P(x, y) = (\lambda x_2 + (1-\lambda) x_1, \lambda y_2 + (1-\lambda) y_1)\]

In the approach where the ratio \(AP:AB = \lambda\), the value of \(\lambda\) directly influences the position of point \(P\) relative to points \(A\) and \(B\) along or beyond the line segment \(AB\):

1. \(\lambda = 0\): Point \(P\) coincides with point \(A\). This corresponds to \(P\) being at the very start of the segment \(AB\).

2. \(0 < \lambda < 1\): Point \(P\) lies between \(A\) and \(B\) on the line segment \(AB\). As \(\lambda\) increases from 0 to 1, \(P\) moves from \(A\) towards \(B\).

3. \(\lambda = 1\): Point \(P\) coincides with point \(B\), marking the end of the segment \(AB\).

4. \(\lambda > 1\): \(P\) divides \(AB\) externally on the side of \(B\). In this scenario, \(P\) is located on the extension of \(AB\) beyond \(B\), indicating that \(P\) is further from \(A\) compared to \(B\).

5. \(\lambda < 0\): \(P\) divides \(AB\) externally on the side of \(A\). Here, \(P\) is positioned on the extension of \(AB\) beyond \(A\), suggesting an external division where \(P\) is closer to \(A\) than to \(B\).

This formulation provides a continuous mapping of \(\lambda\) to positions of \(P\) along and beyond the segment \(AB\), illustrating how changes in \(\lambda\) translate to different locations of \(P\) in relation to \(A\) and \(B\).

Midpoint and points of trisection

Midpoint

Given two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\), the midpoint \(M\) of the line segment \(\overline{AB}\) divides it in the ratio 1:1. Put \(lambda=1\) in the section formula \(M=\frac{\lambda B+A}{\lambda+1}\).Therefore, the coordinates of \(M\) are given by

\[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right). \]

Points of Trisection

Points of trisection of a line segment are the two points that divide the segment into three equal parts. Let \(A(x_1, y_1)\) and \(B(x_2, y_2)\) be the endpoints of the segment. We aim to find the coordinates of the points \(P\) and \(Q\) that trisect the line segment \(\overline{AB}\).

Points of trisection \(P\) and \(Q\) of a line segment into ratio \(1:2\) and \(2:1\) respectively.

Given a line segment \(\overline{AB}\), the section formula for a point dividing this segment in the ratio \(m:n\) is given by the coordinates:

\[ x = \frac{m x_2 + n x_1}{m + n}, \quad y = \frac{m y_2 + n y_1}{m + n} \]

For Point \(P\) (First Trisection Point):

For \(P\) dividing \(\overline{AB}\) in the ratio \(1:2\) (\(m=1\), \(n=2\)), the coordinates \(x_p, y_p\) are calculated as:

\[ x_p = \frac{1 \cdot x_2 + 2 \cdot x_1}{1 + 2}, \quad y_p = \frac{1 \cdot y_2 + 2 \cdot y_1}{1 + 2} \]

Simplifying, we obtain:

\[ x_p = \frac{x_2 + 2x_1}{3}, \quad y_p = \frac{y_2 + 2y_1}{3} \]

For Point \(Q\) (Second Trisection Point):

For \(Q\) dividing \(\overline{AB}\) in the ratio \(2:1\) (\(m=2\), \(n=1\)), the coordinates \(x_q, y_q\) are determined by:

\[ x_q = \frac{2 \cdot x_2 + 1 \cdot x_1}{2 + 1}, \quad y_q = \frac{2 \cdot y_2 + 1 \cdot y_1}{2 + 1} \]

Yielding:

\[ x_q = \frac{2x_2 + x_1}{3}, \quad y_q = \frac{2y_2 + y_1}{3} \]

Harmonic Conjugates

Let \(A(x_1, y_1)\) and \(B(x_2, y_2)\) be two points on a plane. Suppose a point \(P\) divides the line segment \(\overline{AB}\) internally in the ratio \(m:n\), and a point \(Q\) divides the same line segment externally in the same ratio \(m:n\). Then, points \(P\) and \(Q\) are referred to as harmonic conjugates with respect to \(A\) and \(B\).

Internal Division by \(P\)

For internal division, the coordinates of \(P(x_p, y_p)\) are determined using the section formula:

\[ x_p = \frac{m x_2 + n x_1}{m + n}, \quad y_p = \frac{m y_2 + n y_1}{m + n} \]

External Division by \(Q\)

For external division, the coordinates of \(Q(x_q, y_q)\) still follow a similar form but account for the external division by using a negative ratio for \(n\), effectively flipping the sign:

\[ x_q = \frac{m x_2 - n x_1}{m - n}, \quad y_q = \frac{m y_2 - n y_1}{m - n} \]

Given that \(P\) and \(Q\) are harmonic conjugates with respect to \(A(x_1, y_1)\) and \(B(x_2, y_2)\), where \(P\) divides \(AB\) internally in the ratio \(m:n\) and \(Q\) divides \(AB\) externally in the same ratio \(m:n\), we aim to find the ratio \(\lambda:1\) in which \(A\) divides the segment \(PQ\).

Step 1: Expressing \(A\), \(P\), and \(Q\) Using the Section Formula

For \(P\), which internally divides \(AB\), the coordinates are given by:

\[ x_p = \frac{m x_2 + n x_1}{m + n}, \quad y_p = \frac{m y_2 + n y_1}{m + n} \]

For \(Q\), which externally divides \(AB\), the coordinates are:

\[ x_q = \frac{m x_2 - n x_1}{m - n}, \quad y_q = \frac{m y_2 - n y_1}{m - n} \]

Step 2: Ratio in Which \(A\) Divides \(PQ\)

According to the problem, \(A\) divides \(PQ\) in the ratio \(\lambda:1\), implying:

\[ A = \frac{\lambda Q + P}{\lambda + 1} \]

Expanding this for the \(x\)-coordinate (and similarly for \(y\)), we have:

\[ x_1 = \frac{\lambda x_q + x_p}{\lambda + 1} \]

Substituting \(x_p\) and \(x_q\) from above:

\[ x_1 = \frac{\lambda \left( \frac{m x_2 - n x_1}{m - n} \right) + \left( \frac{m x_2 + n x_1}{m + n} \right)}{\lambda + 1} \]

Step 3: Solving for \(\lambda\)

Multiply both sides by \((\lambda + 1)(m - n)(m + n)\) to clear the denominators:

\[ x_1(\lambda + 1)(m^2 - n^2) = \lambda(m x_2 - n x_1)(m + n) + (m x_2 + n x_1)(m - n) \]

On simplification, we get:

\[\lambda = \frac{n-m}{m+n}\]

Similarly it can be proven that \(B\) divides \(PQ\)

Let \(P\) and \(Q\) be harmonic conjugates with respect to points \(A(x_1, y_1)\) and \(B(x_2, y_2)\). If \(P\) divides the segment \(\overline{AB}\) internally and \(Q\) divides the same segment externally, both in the ratio \(m:n\), then \(A\) and \(B\) also serve as harmonic conjugates with respect to \(P\) and \(Q\). Furthermore, \(A\) and \(B\) divide the segment \(\overline{PQ}\) in the ratio \((n-m):(m+n)\).

1. If \(n > m\), then \(A\) divides \(\overline{PQ}\) internally, and \(B\) divides it externally.

   

2. If \(n < m\), then \(A\) divides \(\overline{PQ}\) externally, and \(B\) divides it internally.

   

Applications of Section Formula

Collinearity of Three Points using section formulae

Interestingly, we can verify using section formula whether three points are collinear or not. To verify if three points \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\) are collinear using the section formula, we assume that point \(B\) divides the segment \(\overline{AC}\) in the ratio \(\lambda:1\). The section formula provides a method to calculate the coordinates of a point dividing a line segment internally in a given ratio.

Given that \(B\) divides \(\overline{AC}\) in the ratio \(\lambda:1\), the coordinates of \(B\) can be expressed as:

• For the \(x\)-coordinate:

\[x_2 = \frac{\lambda x_3 + x_1}{\lambda + 1}\]

• For the \(y\)-coordinate:

\[y_2 = \frac{\lambda y_3 + y_1}{\lambda + 1}\]

Isolate \(\lambda\), we rearrange the equations for both \(x_2\) and \(y_2\):

• From the \(x\)-coordinate equation:

\[\lambda = \frac{x_2 - x_1}{x_3 - x_2}\]

• From the \(y\)-coordinate equation:

\[\lambda = \frac{y_2 - y_1}{y_3 - y_2}\]

Now, for the points \(A\), \(B\), and \(C\) to be collinear, the value of \(\lambda\) obtained from the equations involving the \(x\)-coordinates must be equal to the value of \(\lambda\) obtained from the equations involving the \(y\)-coordinates. This is because the ratio of division by \(B\) should be consistent in both dimensions for the points to lie on the same straight line. If the values of \(\lambda\) are not equal, it indicates that the points do not lie on the same straight line, thus not being collinear.

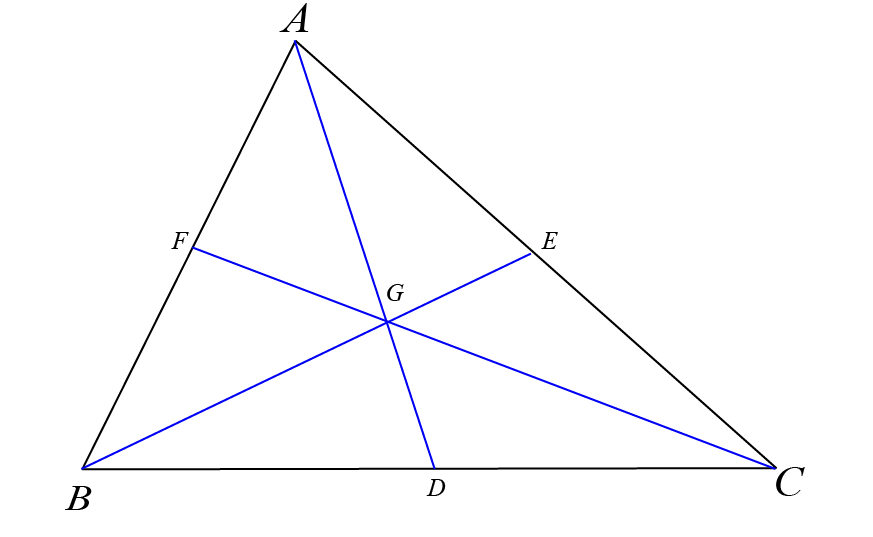
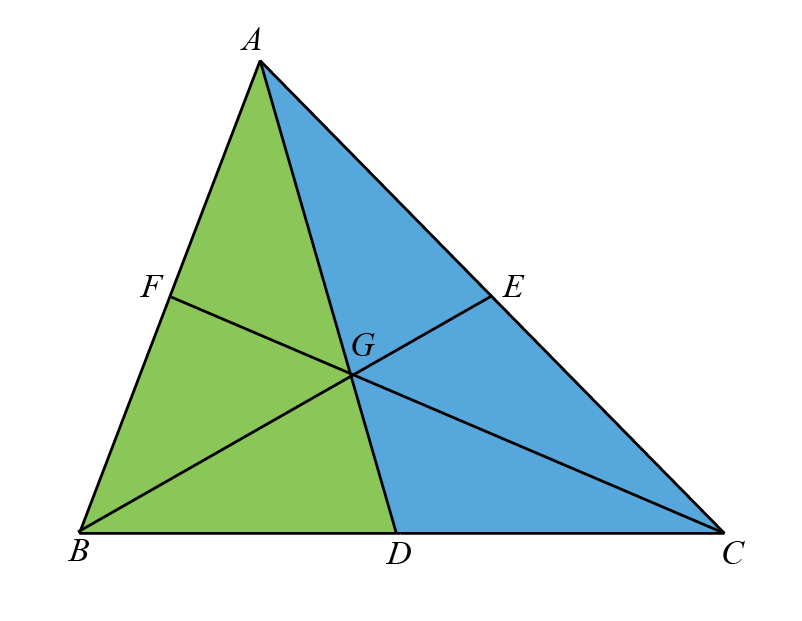
Median

In triangle \(ABC\), a median is a line segment that originates from a vertex and divides the opposite side into two equal parts. Specifically:

• The median from vertex \(A\) meets the midpoint of side \(BC\) at point \(D\), where \(D\) is such that \(BD = DC\).
• The median from vertex \(B\) meets the midpoint of side \(AC\) at point \(E\), where \(AE = EC\).
• The median from vertex \(C\) meets the midpoint of side \(AB\) at point \(F\), where \(AF = FB\).

These medians (\(\overline{AD}\), \(\overline{BE}\), and \(\overline{CF}\)) bisect the sides of the triangle to which they are drawn, and all three intersect at a single point, known as the centroid of the triangle.

A geometrical proof can be easily written for the fact that all three medians intersect in a common point. But we do not wish to because we will prove this using vectors later on.

Length of Median: Apollonius's Theorem

Apollonius's Theorem states that in any triangle \(ABC\), for a median \(AD\) with \(D\) as the midpoint of \(BC\), the relationship between the sides of the triangle and the median is given by:

\[AB^2 + AC^2 = 2(AD^2 + BD^2)\]

Here, \(AD\) is the median, \(BD\) is half the length of \(BC\), and \(AB\), \(AC\) are the lengths of the other two sides of the triangle. This theorem provides a method to compute the length of the median \(AD\) from the known lengths of the sides \(AB\), \(AC\), and the segment \(BD\).

Given that \(a = BC\), \(b = AC\), and \(c = AB\) in triangle \(ABC\), and using Apollonius's Theorem:

\[AB^2 + AC^2 = 2(AD^2 + BD^2)\]

We can express this in terms of \(a\), \(b\), and \(c\):

\[c^2 + b^2 = 2\left(AD^2 + \left(\frac{a}{2}\right)^2\right)\]

To solve for \(AD\), the length of the median from \(A\) to \(D\) (with \(D\) being the midpoint of \(BC\)), we isolate \(AD\):

\[AD^2 = \frac{c^2 + b^2}{2} - \left(\frac{a}{2}\right)^2\]

\[AD^2 = \frac{c^2 + b^2}{2} - \frac{a^2}{4}\]

\[AD^2 = \frac{2(c^2 + b^2) - a^2}{4}\]

Taking the square root of both sides gives us \(AD\):

\[AD = \sqrt{\frac{2(c^2 + b^2) - a^2}{4}}\]

\[AD = \frac{1}{2}\sqrt{2(c^2 + b^2) - a^2}\]

Hence, the length of the median \(AD\) in terms of the sides \(a\), \(b\), and \(c\) of the triangle is:

\[AD = \frac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}\]

Similarly other medians have lengths given by,

\[BE = \frac{1}{2}\sqrt{2a^2 + 2c^2 - b^2}\]

\[CF = \frac{1}{2}\sqrt{2a^2 + 2b^2 - c^2}\]

\[AD = \frac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}\]

\[BE = \frac{1}{2}\sqrt{2a^2 + 2c^2 - b^2}\]

\[CF = \frac{1}{2}\sqrt{2a^2 + 2b^2 - c^2}\]

Centroid

The centroid of triangle \(ABC\) is the point of intersection of its three medians, which are the line segments connecting each vertex to the midpoint of the opposite side.

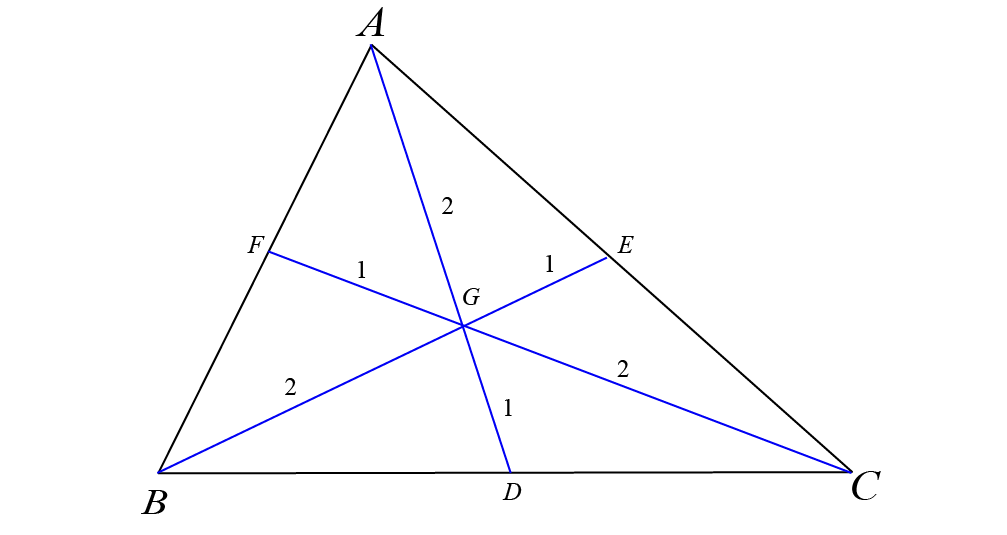
The centroid divides each median in the ratio of 2:1, with the larger segment being between the vertex and the centroid. If \( G \) is the centroid and \( AD \) is a median, then \( AG:GD = 2:1 \). Similarly, the centroid divides medians \( BE \) and \( CF \) in the ratio of \( 2:1 \), with \( BG:GE = 2:1 \) and \( CG:GF = 2:1 \), where \( G \) is closer to vertex \( B \) and vertex \( C \) respectively, than to points \( E \) and \( F \).

Coordinates of the Centroid of a Triangle

Given a triangle \( ABC \) with vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \), the centroid \( G \) of the triangle has coordinates

\[ G\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right). \]

Proof:

Let \( D \) be the midpoint of side \( BC \) of triangle \( ABC \). By definition of a midpoint in Cartesian coordinates,

\[ D\left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}\right). \]

Since the centroid \( G \) divides median \( AD \) in the ratio \( 2:1 \), the coordinates of \( G \) can be found using the section formula in the ratio \( 2:1 \) as follows:

\[ x_G = \frac{2\left(\frac{x_2 + x_3}{2}\right) + x_1}{2 + 1} = \frac{x_1 + x_2 + x_3}{3}, \]

\[ y_G = \frac{2\left(\frac{y_2 + y_3}{2}\right) + y_1}{2 + 1} = \frac{y_1 + y_2 + y_3}{3}. \]

Thus, the centroid \( G \) has coordinates

\[ G\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right). \]

\[ \mathbf{G} = \frac{\mathbf{A} + \mathbf{B} + \mathbf{C}}{3} \]

This concludes the proof.

Some important facts about centroid

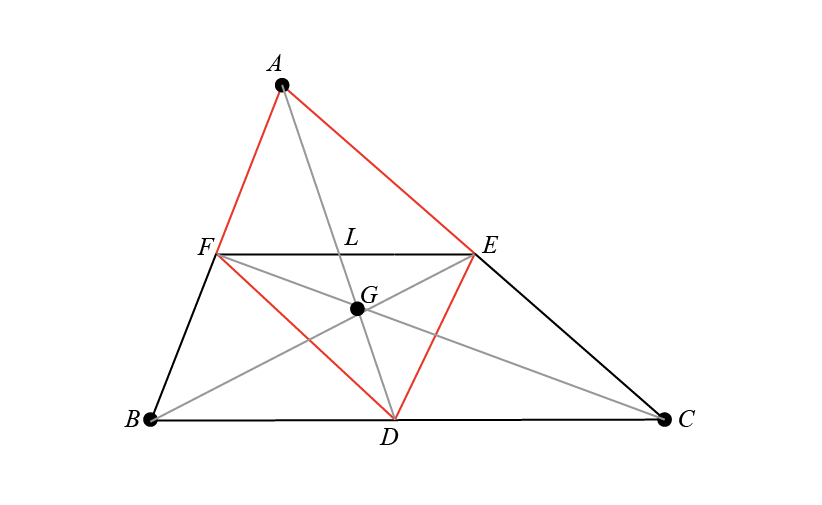
• In triangle \( ABC \), let \( D \), \( E \), and \( F \) be the midpoints of sides \( BC \), \( AC \), and \( AB \), respectively. When segments \( FE \), \( FD \), and \( DE \) are drawn, they create the *medial triangle \( DEF \). By the Midpoint Theorem, segment \( FE \) is parallel to \( BC \), segment \( FD \) is parallel to \( AC \), and segment \( DE \) is parallel to \( AB \). This theorem states that a line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. Therefore, medial triangle \( DEF \) is formed, whose sides are parallel to the respective sides of triangle \( ABC \) and half as long.

• The quadrilateral \(AFDE\) is a parallelogram. This is due to the fact that \(FD\) and \(AE\) are both parallel and equal to half of length of \(BC\) (as \(FD\) and \(AE\) are each half the length of \(BC\) by the Midpoint Theorem), and \(AF\) and \(DE\) are both parallel and equal to half of length of \(AB\) (again by the Midpoint Theorem).

  Within parallelogram \(AFDE\), diagonals \(AD\) and \(FE\) bisect each other at point \(L\). According to the properties of parallelograms, the diagonals bisect each other, meaning \(L\) is the midpoint of both \(AD\) and \(FE\). Therefore, by the midpoint formula, \(L\) is calculated as:

  \[ L = \frac{A + D}{2} = \frac{F + E}{2} \]

  From this, we deduce that vertex \(A\) can be found using the coordinates of \(D\), \(E\), and \(F\):

  \[ A = F + E - D \]

  To find the coordinates of vertices \(B\) and \(C\), we apply similar logic, considering parallelograms formed by other pairs of triangle medians:

  \[ B = D + F - E \]
  \[ C = E + D - F \]

  This method is effective for calculating the vertices of a triangle when the midpoints of its sides are known.

  Example

  Given the midpoints \( D(1, 2) \), \( E(-3, 4) \), and \( F(-5, -3) \), the vertices of triangle \( ABC \) can be calculated using the relationships established by the properties of parallelograms within the triangle. According to these properties:

  Vertex \( A \) can be found as \( A = F + E - D \):

  \[ A_x = F_x + E_x - D_x = (-5) + (-3) - (1) = -9 \]

  \[ A_y = F_y + E_y - D_y = (-3) + (4) - (2) = -1 \]

  So, \( A \) is at \( (-9, -1) \).

  Vertex \( B \) is found as \( B = D + F - E \):

  \[ B_x = D_x + F_x - E_x = (1) + (-5) - (-3) = -1 \]

  \[ B_y = D_y + F_y - E_y = (2) + (-3) - (4) = -5 \]

  So, \( B \) is at \( (-1, -5) \).

  Vertex \( C \) is calculated as \( C = E + D - F \):

  \[ C_x = E_x + D_x - F_x = (-3) + (1) - (-5) = 3 \]

  \[ C_y = E_y + D_y - F_y = (4) + (2) - (-3) = 9 \]

  So, \( C \) is at \( (3, 9) \).

  The vertices of triangle \( ABC \) are thus \( A(-9, -1) \), \( B(-1, -5) \), and \( C(3, 9) \).

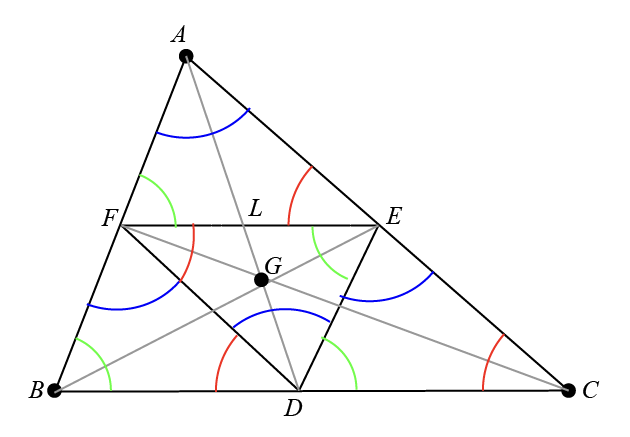
• Triangles \( AFE \), \( BDF \), and \( CDE \) are congruent to triangle \( DEF \).

  

  The congruency of these triangles can be established through the following properties:

  1. Parallel Sides: Each side of triangle \( DEF \) is parallel to one side of triangle \( ABC \).

  2. Proportional Sides: Because the medians divide the sides of triangle \( ABC \) into segments of equal length, the corresponding sides of triangles \( AFE \), \( BDF \), and \( CDE \) are equal to each other and half the length of the sides of triangle \( ABC \).

  3. Equal Angles: The angles of triangles \( AFE \), \( BDF \), and \( CDE \) are equal to the corresponding angles in triangle \( DEF \) because they are alternate interior angles created by transversal lines cutting parallel lines.

  These properties result in triangles \( AFE \), \( BDF \), \( CDE \), and \( DEF \) all being congruent.

• Given that triangles \( AFE \), \( BDF \), \( CDE \), and \( DEF \) are congruent, it follows that their areas are equal and thus,

  \[ \text{Area}(DEF) = \text{Area}(AFE) = \text{Area}(BDF) = \text{Area}(CDE) = \frac{1}{4}\text{Area}(ABC) \]

• Area of triangle \(ABD\) is equal to the area of triangle \(ACD\) because \(D\) is the midpoint of \(BC\), making \(AD\) and \(DC\) equal in length, and both triangles share the same height from \(A\) perpendicular to \(BC\).

  

  Similarly, the area of triangle \(BEC\) is equal to the area of triangle \(AEB\) because \(E\) is the midpoint of \(AC\), making \(BE\) and \(AE\) equal in length, with both triangles sharing the same height from \(B\) perpendicular to \(AC\).

  Finally, the area of triangle \(AFC\) is equal to the area of triangle \(AFB\) because \(F\) is the midpoint of \(AB\), making \(CF\) and \(BF\) equal in length, with both triangles sharing the same height from \(C\) perpendicular to \(AB\).

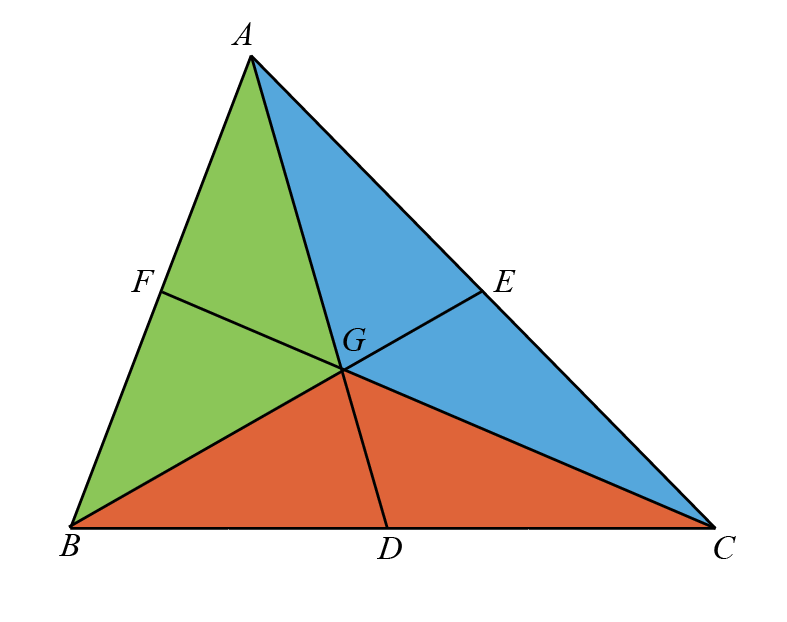
• In any triangle \(ABC\), where \(G\) is the centroid, the medians of the triangle divide it into three smaller triangles, \(AGB\), \(AGC\), and \(BGC\), that have equal areas.

  

  Proof:

  To prove that Area(\(AGB\)) = Area(\(AGC\)), we proceed as follows:

  1. Show that Area(\(BGD\)) = Area(\(CGD\)): Since \(D\) is the midpoint of \(BC\), \(BD = DC\), and \(GD\) is common to both triangles \(BGD\) and \(CGD\), the two triangles have the same base and height, hence the same area.

  2. Knowing that Area(\(ABD\)) = Area(\(ACD\)) (since \(AD\) is a median): Each of these areas is half of the entire triangle \(ABC\), as a median divides a triangle into two triangles of equal area.

  3. The area of \(AGB\) can be expressed as Area(\(ABD\)) - Area(\(BGD\)), and similarly, the area of \(AGC\) as Area(\(ACD\)) - Area(\(CGD\)).

  Thus, because Area(\(ABD\)) = Area(\(ACD\)) and Area(\(BGD\)) = Area(\(CGD\)), subtracting equal areas from equal areas gives us Area(\(AGB\)) = Area(\(AGC\)).

  Similarly, we can prove that Area(\(AGC\)) = Area(\(BGC\)) by observing that both triangles \(AGC\) and \(BGC\) share the common base \(GC\) and have the same height from vertex \(B\) and \(A\) respectively to line \(GC\).

  Thus, since Area(\(AGB\)) = Area(\(AGC\)) and Area(\(AGC\)) = Area(\(BGC\)), it follows that all three triangles \(AGB\), \(AGC\), and \(BGC\) have equal areas. This demonstrates that the medians of a triangle not only bisect the area of the triangle but also partition the triangle into six smaller triangles of equal area. \(\blacksquare\)

• Coincidence of Centroids of Triangle \( ABC \) and Medial Triangle \( DEF \)

  The centroid of triangle \( ABC \) and the centroid of the medial triangle \( DEF \), formed by the midpoints \( D \), \( E \), and \( F \) of the sides \( BC \), \( AC \), and \( AB \) of triangle \( ABC \), are the same point.

  Proof:

  1. Construct parallelogram \( AFDE \) as previously discussed, where \( AF \) and \( DE \) are parallel, as are \( AD \) and \( FE \).

  2. Diagonals \( AD \) and \( FE \) of parallelogram \( AFDE \) intersect at point \( L \), bisecting each other.

  3. Since \( L \) is the midpoint of \( FE \), and \( FE \) is a side of triangle \( DEF \), segment \( DL \) is a median of triangle \( DEF \).

  4. Median \( AD \) of triangle \( ABC \) coincides with median \( DL \) of triangle \( DEF \), as they are collinear and share the common midpoint \( L \).

  5. Similarly, median \( BE \) of triangle \( ABC \) is collinear with median \( EL \) of triangle \( DEF \), and median \( CF \) of triangle \( ABC \) with median \( FL \) of triangle \( DEF \).

  6. The three medians of triangle \( ABC \) intersect at the centroid \( G \), which, by the collinearity established in steps 3 and 4, must also be the point where the medians of triangle \( DEF \) intersect.

  7. Therefore, the centroid \( G \) of triangle \( ABC \) is also the centroid of the medial triangle \( DEF \).

  By this proof, we have established that the centroids of both triangle \( ABC \) and its medial triangle \( DEF \) are the same point.

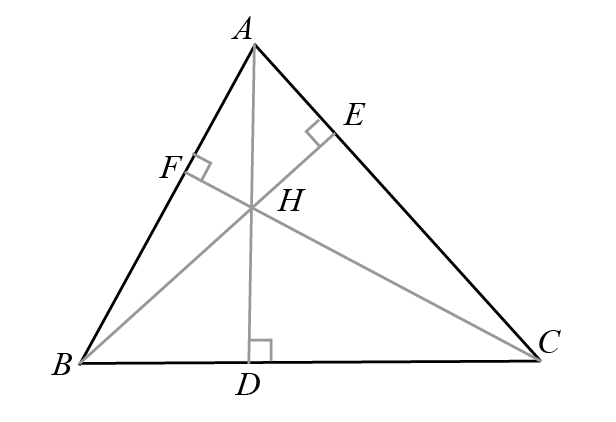
Orthocentre

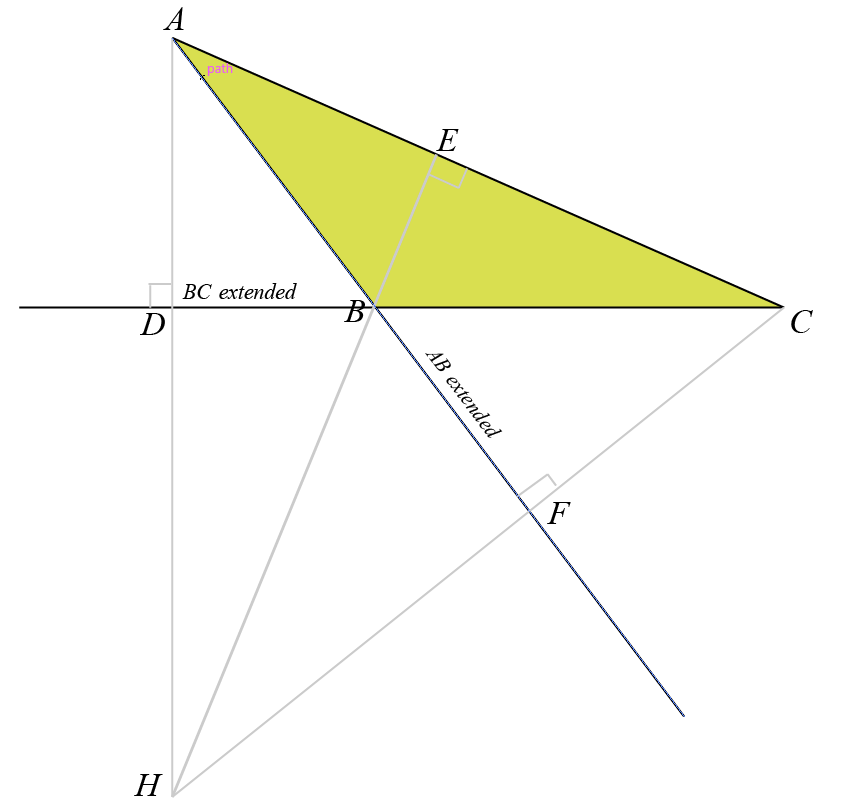
The orthocenter of a triangle is the point where the three altitudes intersect. An altitude of a triangle is a line which passes through a vertex of the triangle and is perpendicular to the opposite side.

In triangle \( ABC \), let the altitudes from vertices \( A \), \( B \), and \( C \) be \( AD \), \( BE \), and \( CF \), respectively. The point of intersection of these altitudes is denoted as \( H \), which is the orthocenter of the triangle.

The orthocenter of a triangle, denoted by \( H \), is the common point of intersection of the triangle's three altitudes. An altitude is a perpendicular segment from a vertex to the line containing the opposite side. The location of the orthocenter relative to the triangle depends on the type of triangle:

1. Acute Triangle: For an acute triangle, where all angles are less than 90 degrees, the orthocenter lies inside the triangle. This is because each altitude will be internal when drawn from a vertex to the opposite side.

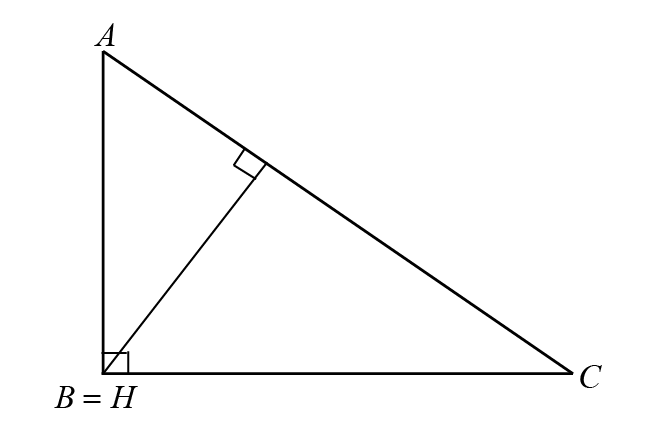
2. Right Triangle: In a right triangle, the orthocenter coincides with the vertex of the right angle. This happens because the sides of the triangle itself serve as altitudes: one altitude is the vertical side, another is the horizontal side, and the third is the line segment from the right angle vertex to the hypotenuse, which is already perpendicular by definition.

3. Obtuse Triangle: For an obtuse triangle, which has an angle greater than 90 degrees, the orthocenter falls outside the triangle. To draw the altitudes, extensions of the sides are needed since the perpendicular lines from the vertices opposite the obtuse angle will fall outside the triangle.

In any triangle \( ABC \) with altitudes \( AD \), \( BE \), and \( CF \), the point where these three altitudes meet is the orthocenter \( H \). To find \( H \) computationally or constructively, it typically requires only two altitudes; their intersection defines the orthocenter's exact location.

ACUTE TRIANGLE

RIGHT ANGLED TRIANGLE

OBTUSE TRIANGLE

Orthocenters of Triangles Formed by Orthocenter and Vertices

In triangle \( ABC \), if \( H \) is the orthocenter, then \( A \) is the orthocenter of triangle \( HBC \), \( B \) is the orthocenter of triangle \( HCA \), and \( C \) is the orthocenter of triangle \( HAB \).

Proof:

1. \( HD \) is an altitude of \( \triangle ABC \) because \( H \) is the orthocenter, implying \( HD \perp BC \).
2. \( HD \) is also an altitude of \( \triangle HBC \) since it is coincident with \( AD \) of \( \triangle ABC \) and lies on \( A \), one of the vertices of \( \triangle HBC \).

Similarly, for \( \triangle HCA \) and \( \triangle HAB \):

1. \( BE \) is the altitude of \( \triangle ABC \) extended through \( H \), which implies \( BE \perp AC \) and \( CE \) is the altitude of \( \triangle HCA \).
2. \( CF \) is the altitude of \( \triangle ABC \) extended through \( H \), which implies \( CF \perp AB \) and \( BF \) is the altitude of \( \triangle HAB \).

Since the altitudes of \( \triangle ABC \) serve as altitudes for \( \triangle HBC \), \( \triangle HCA \), and \( \triangle HAB \) respectively, through coincident lines, this establishes that \( A \), \( B \), and \( C \) serve as orthocenters for these triangles respectively.

Pedal Triangle amd Orthic Triangle

The pedal triangle \( DEF \) of a point \( P \) relative to \( \triangle ABC \) is the triangle formed by the points \( D \), \( E \), and \( F \), which are the feet of the perpendiculars from \( P \) to the sides \( BC \), \( CA \), and \( AB \) of \( \triangle ABC \), respectively.

• \( PD \perp BC \)
• \( PE \perp AC \)
• \( PF \perp AB \)

If \( P \) coincides with the orthocenter \( H \) of \( \triangle ABC \), then \( D \), \( E \), and \( F \) are the feet of the altitudes of \( \triangle ABC \), and the pedal triangle \( DEF \) is also known as the orthic triangle of \( \triangle ABC \).

Incentre

The incenter of a triangle \( ABC \) is the point from which the incircle, the unique circle that touches each of the sides \( AB \), \( BC \), and \( CA \) internally, is centered. The points where the incircle touches the sides are called the points of tangency, and they lie directly on the sides \( AB \), \( BC \), and \( CA \), equidistant from the incenter. The radius of the incircle is perpendicular to each side of the triangle at these points of tangency.

In triangle \( ABC \), the incircle is tangent to the sides at points \( D \), \( E \), and \( F \). The center of this incircle is the incenter, denoted as \( I \). The radius of the incircle, such as \( ID \), is perpendicular to the side it touches, in this case, side \( BC \).

Since the segments \( AE \) and \( AF \) are equal in length, being tangents to the incircle from the same external point \( A \), triangles \( AIE \) and \( AIF \) are congruent by the Side-Side-Side postulate. This congruency implies that angle \( IAC \) is equal to angle \( IAB \), which establishes that \( AI \) is the angle bisector of angle \( A \).

Similarly, because the incircle is tangent to \( AB \) at \( F \) and \( AC \) at \( E \), and the tangents from a common external point to a circle are equal, we can deduce that \( BI \) and \( CI \) bisect angles \( B \) and \( C \) respectively.

Thus, the incenter \( I \) can also be defined as the single point at which the three internal angle bisectors of triangle \( ABC \) intersect.

Coordinates of Incentre

The coordinates of the incenter \( I \) of triangle \( ABC \), with vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \) and side lengths \( a = BC \), \( b = AC \), and \( c = AB \), can be found using the formula:

\[ I \left( \frac{ax_1 + bx_2 + cx_3}{a+b+c}, \frac{ay_1 + by_2 + cy_3}{a+b+c} \right) \]

Proof:

To prove the formula for the incenter \( I \) of a triangle \( ABC \), we can employ the Angle Bisector Theorem. This theorem states that an angle bisector in a triangle divides the opposite side into two segments that are proportional to the lengths of the other two sides.

Given:

• Triangle \( ABC \) with side lengths \( AB = c \), \( AC = b \), and \( BC = a \).
• Vertices of the triangle are \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).

We proceed as follows:

Step 1: Applying the Angle Bisector Theorem to \( AL \)

The angle bisector theorem states that the angle bisector divides the opposite side in the ratio of the adjacent sides. If \( AL \) is the angle bisector of \( \angle A \), it divides side \( BC \) into two segments, \( BD \) and \( DC \), such that \( BD:DC = AB:AC = c:b \). Since we know the coordinates of \( B \) and \( C \), we can find the coordinates of \( D \) as:

\[ D\left(\frac{cx_3 + bx_2}{b + c}, \frac{cy_3 + by_2}{b + c}\right) \]

Step 2: Length of Segment \( AL \)

Using the section formula, the length of segment \( AL \), which is in the ratio \( c:b \) to side \( BC \), can be expressed as:

[ AL = \frac{c}{b + c} \cdot BC ] [ BC ] can be found by the distance formula, and then \( AL \) can be calculated.

Step 3: Apply the Angle Bisector Theorem to \( \triangle ABL \)

Similarly, \( BI \) is the angle bisector in \( \triangle ABL \), and it divides \( AL \) in the ratio of \( AB:BL \). Given that \( AB \) is to \( BL \) as \( c \) is to \( ac/(b+c) \), we have \( AI:IL = (b+c):a \).

The coordinates of \( I \) are found by dividing the segment \( AL \) in the ratio \( (b+c):a \) starting from \( A \) to \( L \). If \( L \) is the point on segment \( AL \) at which \( BI \) intersects \( AL \), then \( I \) can be determined by the section formula:

\[ I\left(\frac{ax_1 + (b+c)x_{\text{D}}}{a + b + c}, \frac{ay_1 + (b+c)y_{\text{D}}}{a + b + c}\right) \]

Substitute the coordinates of \( D \) from Step 1 into this equation to get the coordinates of the incenter \( I \).

\[ I = \left(\frac{ax_1 + (b+c)\frac{cx_3 + bx_2}{b + c}}{a + b + c}, \frac{ay_1 + (b+c)\frac{cy_3 + by_2}{b + c}}{a + b + c}\right) \]

Now we simplify the expressions for the coordinates of \( I \):

\[ I = \left(\frac{ax_1 + cx_3 + bx_2}{a + b + c}, \frac{ay_1 + cy_3 + by_2}{a + b + c}\right) \]

Thus, the coordinates of \( I \) are obtained by the formula above, giving us the incenter of triangle \( ABC \) in terms of the vertices coordinates \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \) and the lengths of the sides opposite these vertices, \( a \), \( b \), and \( c \).

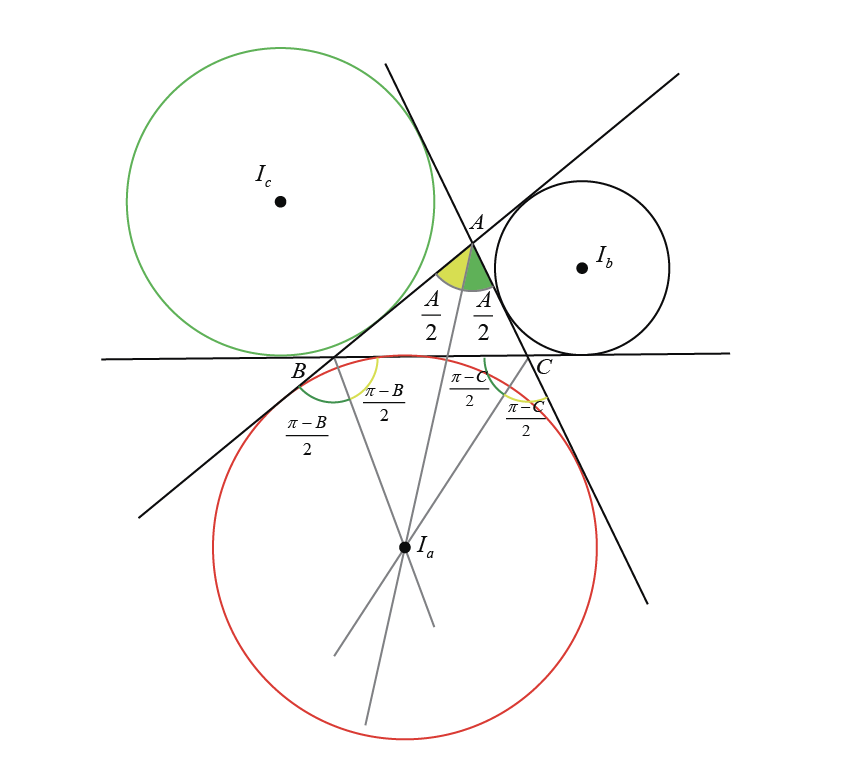
Excentres

Excenters of a triangle are the centers of the escribed circles, which are circles tangent to one side of the triangle and to the extensions of the other two sides. Each triangle has three excenters, corresponding to each of the triangle's vertices.

To construct an excenter, you need to extend the bisector of one interior angle and the bisectors of the exterior angles at the other two vertices. The point where these three lines intersect is the excenter.

For a triangle \(ABC\), the excenters are often denoted as \(I_a\), \(I_b\), and \(I_c\), opposite to the vertices \(A\), \(B\), and \(C\), respectively.

Formulas for excenters: Given the vertices \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\), and sides \(a\), \(b\), and \(c\) opposite these vertices, the coordinates of the excenters \(I_a\), \(I_b\), and \(I_c\) can be found using similar constructions as the incenter but using the exterior angle bisectors. The formulas are as follows:

• Excenter \(I_a\) opposite of vertex \(A\) and corresponding to side \(a\):

\[ I_a = \left( \frac{-ax_1 + bx_2 + cx_3}{-a + b + c}, \frac{-ay_1 + by_2 + cy_3}{-a + b + c} \right) \]

• Excenter \(I_b\) opposite of vertex \(B\) and corresponding to side \(b\):

\[ I_b = \left( \frac{ax_1 - bx_2 + cx_3}{a - b + c}, \frac{ay_1 - by_2 + cy_3}{a - b + c} \right) \]

• Excenter \(I_c\) opposite of vertex \(C\) and corresponding to side \(c\):

\[ I_c = \left( \frac{ax_1 + bx_2 - cx_3}{a + b - c}, \frac{ay_1 + by_2 - cy_3}{a + b - c} \right) \]

These formulas are based on the concept that to locate an excenter, you must consider the lengths of the sides with respect to the angles being bisected. For example, for the excenter \(I_a\), the angle bisector of \(A\) is extended outside the triangle to form the exterior angle, and then the lengths of the other sides are considered with their signs changed accordingly.

[We will study in more detail in the chapter Solutions of Triangle]

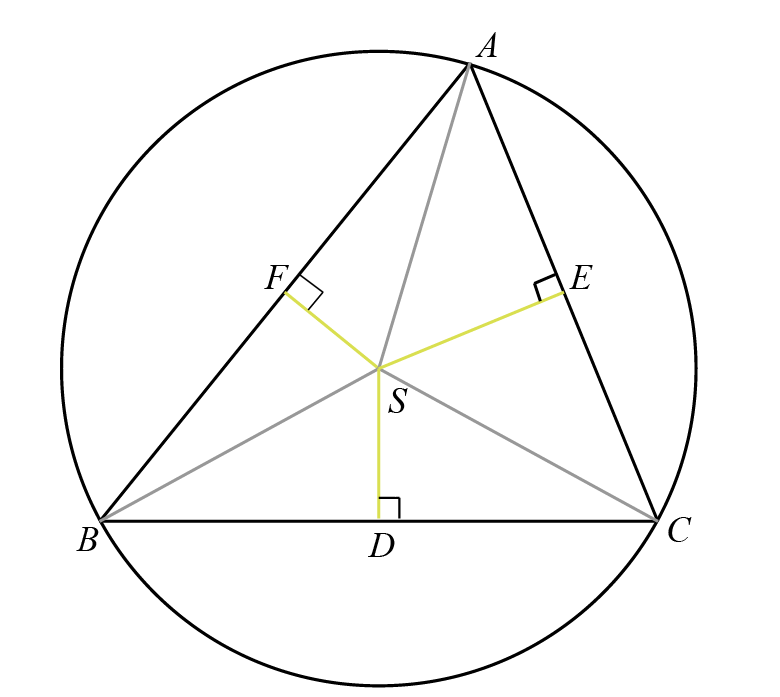
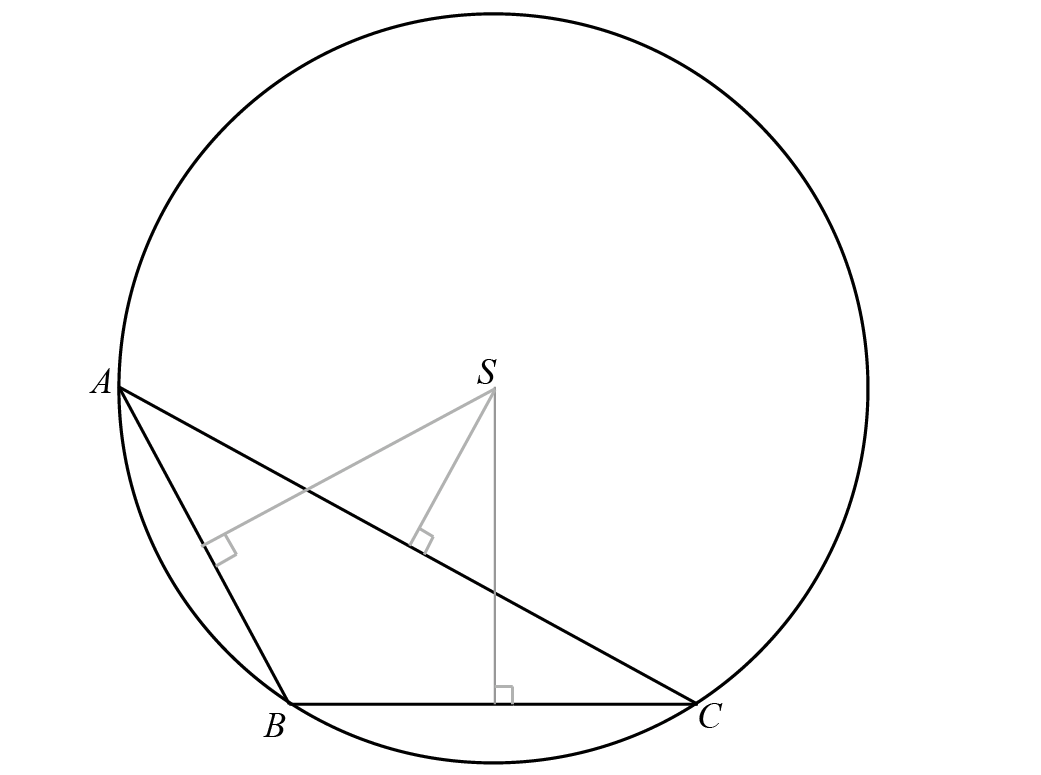
Circumcentre

The circumcircle of a triangle is the unique circle that passes through all three vertices of the triangle. The center of this circle is known as the circumcenter, and its radius is called the circumradius.

The figure illustrates triangle \( ABC \) inscribed in its circumcircle. Point \( S \) represents the circumcenter of the triangle. Perpendiculars \( SD \), \( SE \), and \( SF \) are dropped from \( S \) to the sides \( BC \), \( AC \), and \( AB \) respectively, bisecting each side. This bisecting property stems from the fact that a perpendicular drawn from the center of a circle to any chord of the circle bisects the chord. Consequently, the circumcenter \( S \) can also be defined as the intersection point of the perpendicular bisectors of the sides of the triangle.

Additionally, the lengths \( SA \), \( SB \), and \( SC \) are congruent as they are radii of the circumcircle. This equality is crucial for determining the location of \( S \) when the coordinates of \( A \), \( B \), and \( C \) are known. The circumcenter is equidistant from all vertices of the triangle.

Example

Find the circumcenter \( S(\alpha, \beta) \) of the triangle \( ABC \) with vertices \( A(2,5) \), \( B(-5,3) \), and \( C(0,-4) \).

Solution:

Given vertices: \( A(2,5) \), \( B(-5,3) \), and \( C(0,-4) \)

Let \( S(\alpha, \beta) \) be the circumcenter.

Equations based on radii equality:

\( SA = SC \)

\( SB = SC \)

From \( SA = SC \), we get the equation of the perpendicular bisector of \( AC \):

\[ (\alpha - 2)^2 + (\beta - 5)^2 = (\alpha - 0)^2 + (\beta + 4)^2 \]

Expanding and simplifying, we get:

\[ \alpha^2 - 4\alpha + 4 + \beta^2 - 10\beta + 25 = \alpha^2 + \beta^2 + 8\beta + 16 \]

\[ -4\alpha - 18\beta = -13 \quad \rightarrow \quad 4\alpha + 18\beta + 13 = 0 \quad \ldots \text{(i)} \]

From \( SB = SC \), we get the equation of the perpendicular bisector of \( BC \):

\[ (\alpha + 5)^2 + (\beta - 3)^2 = (\alpha - 0)^2 + (\beta + 4)^2 \]

Expanding and simplifying, we get:

\[ \alpha^2 + 10\alpha + 25 + \beta^2 - 6\beta + 9 = \alpha^2 + \beta^2 + 8\beta + 16 \]

\[ 10\alpha - 14\beta = -18 \quad \rightarrow \quad 10\alpha - 14\beta + 18 = 0 \quad \ldots \text{(ii)} \]

For the system of equations:

\[ 4\alpha + 18\beta + 13 = 0 \quad \text{(i)} \]

\[ 10\alpha - 14\beta + 18 = 0 \quad \text{(ii)} \]

We use the formulas:

\[ \alpha = \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1}, \quad \beta = \frac{a_1 c_2 - a_2 c_1}{a_1 b_2 - a_2 b_1} \]

For (i) \( a_1 = 4 \), \( b_1 = 18 \), \( c_1 = 13 \).

For (ii) \( a_2 = 10 \), \( b_2 = -14 \), \( c_2 = 18 \).

Now we calculate:

\[ \alpha = \frac{(13)(-14) - (18)(18)}{(4)(-14) - (10)(18)} = \frac{-182 - 324}{-56 - 180} = \frac{-506}{-236} = \frac{253}{118} \]

\[ \beta = \frac{(4)(18) - (10)(13)}{(4)(-14) - (10)(18)} = \frac{72 - 130}{-56 - 180} = \frac{-58}{-236} = \frac{29}{118} \]

The circumcenter \( S \) of triangle \( ABC \) has coordinates:

\[ S\left(\frac{253}{118}, \frac{29}{118}\right) \]

Circumcentre of a right angled triangle

For a right-angled triangle, the circumcenter lies at the midpoint of the hypotenuse, and the circumradius is equal to half of the length of hypotenuse.

Proof:

In the figure, the triangle is right-angled at \( A \). To prove that the circumcenter is the midpoint of the hypotenuse \( AB \), draw the perpendicular bisector of \( AB \) passing through point \( P \). Since this bisector is parallel to \( AC \) (as \( AC \) is also perpendicular to \( AB \)), by the Midpoint Theorem, it must also bisect the hypotenuse at \( S \). Similarly, the perpendicular bisector of \( AC \) bisects the hypotenuse at \( S \). Since both these bisectors intersect at \( S \), \( S \) must be the circumcenter.

Location of circumcentre

The circumcenter of a triangle may lie inside, on, or outside the triangle depending on the type of triangle:

• Acute Triangle: The circumcenter lies inside the triangle. This is because the perpendicular bisectors of the sides intersect at a point that is equidistant from all the vertices, which will be within the bounds of the triangle.

• Right Triangle: The circumcenter lies on the triangle, specifically on the midpoint of the hypotenuse. In a right triangle, the hypotenuse serves as the diameter of the circumcircle.

• Obtuse Triangle: The circumcenter lies outside the triangle. In an obtuse triangle, the perpendicular bisectors of the sides will intersect at a point outside the triangle, as the angle opposite the longest side (which is obtuse) requires the circumcenter to fall outside to be equidistant from all three vertices. See the figure below:

Some Miscellaneuous Facts based on centres of Circle

Image Orthocentre in sides

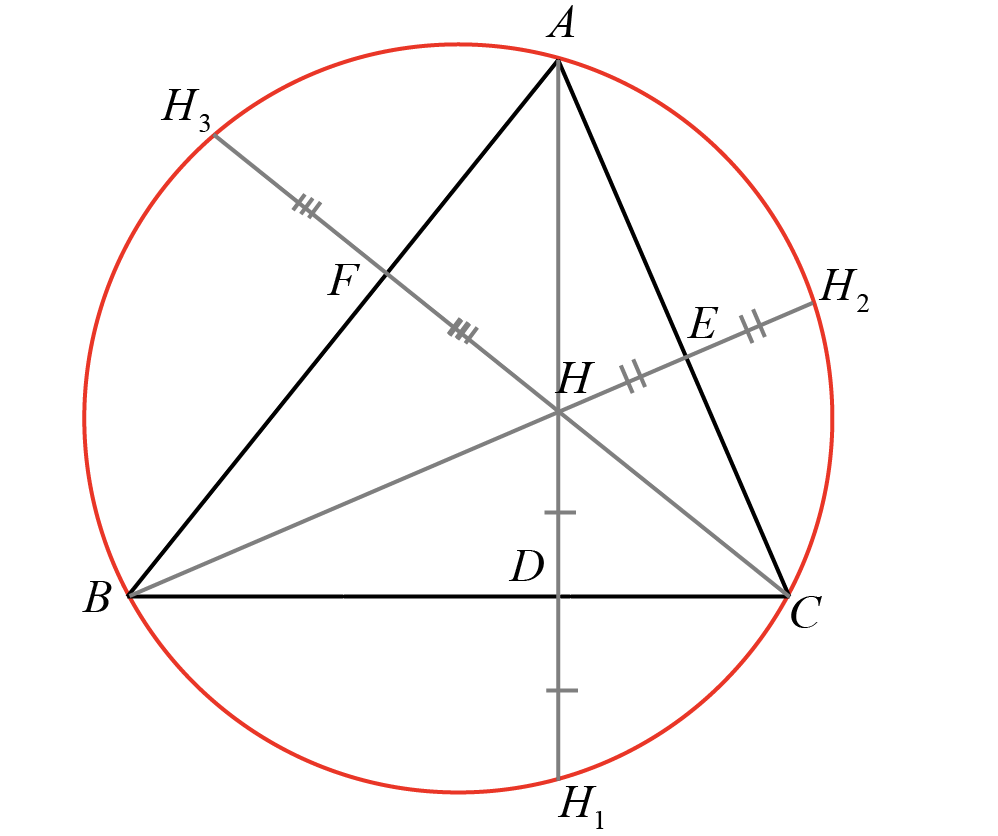
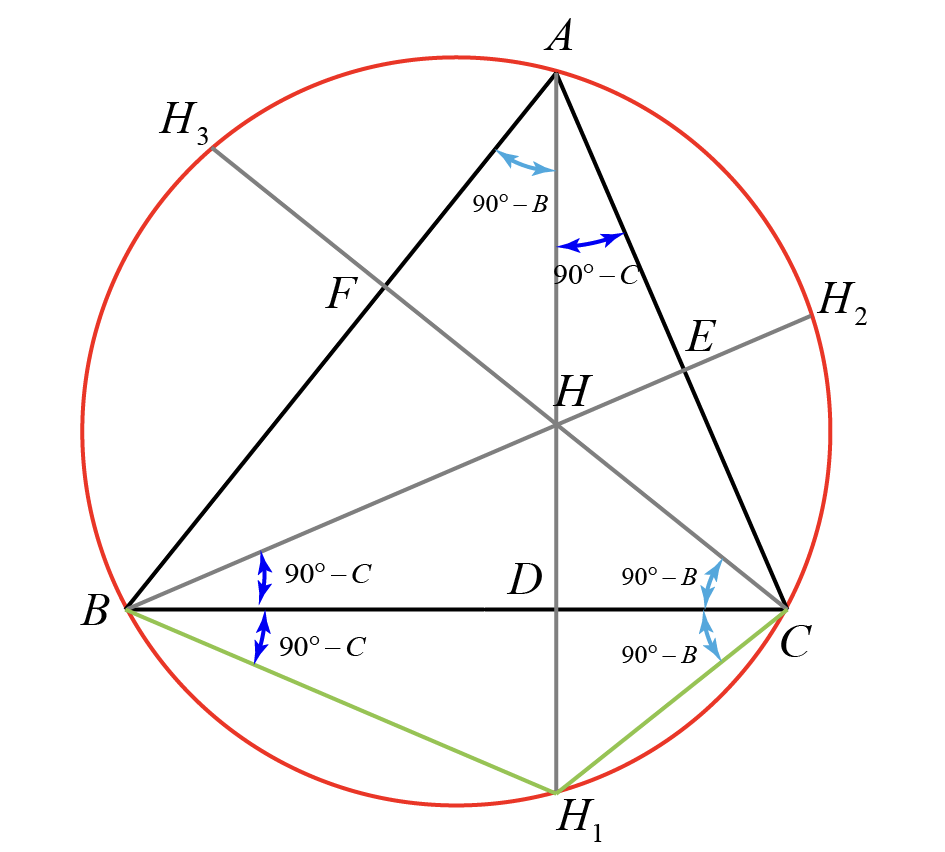
In triangle \( ABC \), let \( H \) be the orthocenter, and let \( H_1 \), \( H_2 \), and \( H_3 \) be the reflections of \( H \) over sides \( BC \), \( CA \), and \( AB \), respectively. Then, points \( H_1 \), \( H_2 \), and \( H_3 \) lie on the circumcircle of triangle \( ABC \).

The figure displays triangle \( ABC \), with \( AD \), \( BE \), and \( CF \) representing the altitudes from vertices \( A \), \( B \), and \( C \), respectively. These altitudes intersect at point \( H \), known as the orthocenter of the triangle. The triangle is inscribed in a circle, known as the circumcircle. The points \( H_1 \), \( H_2 \), and \( H_3 \) are depicted on the sides \( BC \), \( CA \), and \( AB \), respectively, and are the reflections of the orthocenter \( H \) across the respective sides of the triangle.

Proof:

To prove that \( H_1 \), \( H_2 \), and \( H_3 \) are the images of the orthocenter \( H \) in the sides of \( \triangle ABC \), begin by joining \( H_1B \) and \( H_1C \).

In \( \triangle ABD \), which is right-angled at \( D \), \( \angle BAD = 90^\circ - B \). The chord \( H_1B \) subtends \( \angle BAD \) at \( B \) and therefore must subtend the same angle at \( C \), which implies that \( \angle BCH_1 = 90^\circ - B \). Also, in \( \triangle BFC \), which is right-angled at \( F \), \( \angle BCF = 90^\circ - C \), and so \( \angle HCB = \angle H_1CB = 90^\circ - C \). Similarly, it can be shown that \( \angle HBD = \angle H_1BD = 90^\circ - B \).

Thus, by the ASA congruence criterion, \( \triangle HBC \) is congruent to \( \triangle H_1BC \), with \( BC \) being the common side. It follows that \( HD = DH_1 \), confirming that \( H_1 \) is the image of \( H \) in \( BC \). Similar arguments would show that \( H_2 \) and \( H_3 \) are the images of \( H \) in sides \( CA \) and \( AB \), respectively.

Pedal Triangle

In triangle \( ABC \), let point \( P \) be an arbitrary point. The pedal triangle of point \( P \) with respect to triangle \( ABC \) is constructed by dropping perpendiculars from \( P \) to the sides \( AB \), \( BC \), and \( CA \). These perpendiculars meet the sides of \( ABC \) at points \( D \), \( E \), and \( F \) respectively, which are the vertices of the pedal triangle \( DEF \).

The pedal triangle can be classified as follows based on the location of point \( P \):

• When \( P \) is the orthocenter of triangle \( ABC \), the pedal triangle \( DEF \) is known as the orthic triangle. Points \( D \), \( E \), and \( F \) are the feet of the altitudes of \( ABC \).

• If \( P \) is the centroid of triangle \( ABC \), the pedal triangle \( DEF \) is termed the medial triangle. Points \( D \), \( E \), and \( F \) are the midpoints of the sides \( BC \), \( CA \), and \( AB \) respectively.

• When \( P \) is the incenter of triangle \( ABC \), the pedal triangle \( DEF \) is referred to as the intouch triangle. In this case, \( D \), \( E \), and \( F \) are the points of tangency of the incircle with the sides \( BC \), \( CA \), and \( AB \).

When point \( P \) lies on the circumcircle of triangle \( ABC \), the feet of the perpendiculars from \( P \) to the sides of \( ABC \), namely points \( D \), \( E \), and \( F \), become collinear. This specific line on which \( D \), \( E \), and \( F \) lie is known as the Simson line, after Robert Simson.

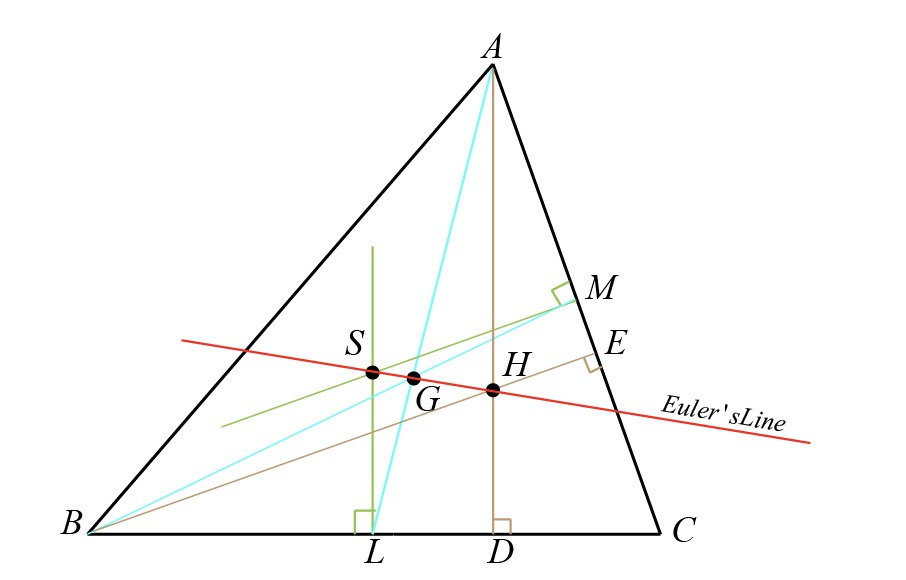
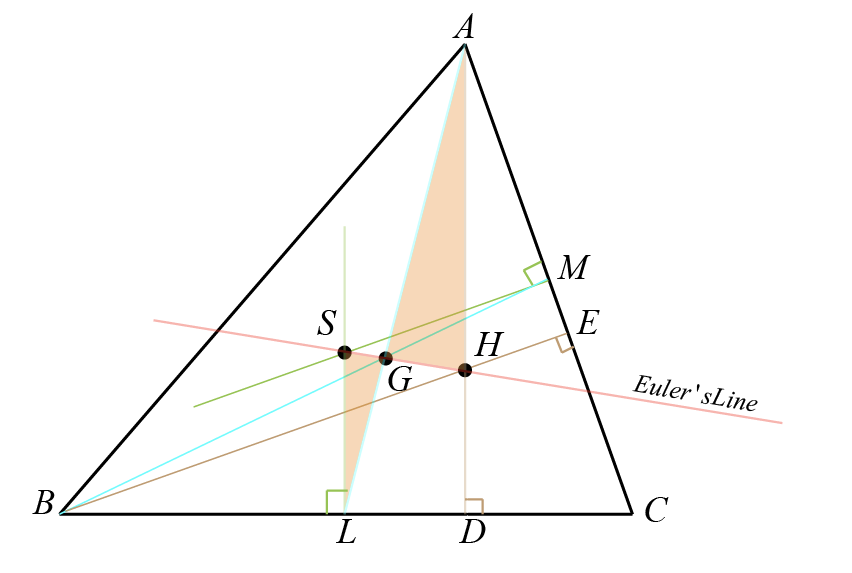
Euler's Line

In triangle \( ABC \), Euler's line is defined as the straight line that passes through several of the triangle's important centers: the centroid \( G \), the orthocenter \( H \), and the circumcenter \( S \).

The distances between these points are related in a fixed ratio. The centroid \( G \) divides the segment from the orthocenter \( H \) to the circumcenter \( S \) in the ratio 2:1. This means that \( HG:GS = 2:1 \). The centroid is twice as far from the orthocenter as it is from the circumcenter.

In the figure of triangle \( ABC \), Euler's line is illustrated by the red line intersecting the orthocenter \( H \), the centroid \( G \), and the circumcenter \( S \).

The orthocenter \( H \) is where the altitudes of the triangle meet, specifically altitudes \( AD \) and \( BE \), and the third altitude (not shown) would also converge at \( H \).

The centroid \( G \) is found at the intersection of the medians of the triangle, with medians \( AL \) and \( BM \) shown intersecting at \( G \). The third median from vertex \( C \) (not depicted) would also intersect at \( G \).

The circumcenter \( S \) is the point of intersection of the perpendicular bisectors of the triangle's sides. The perpendicular bisectors through points \( L \) and \( M \) are shown intersecting at \( S \). The perpendicular bisector of the third side (not labeled) would also pass through \( S \).

Euler's line connects points \( H \), \( G \), and \( S \), affirming their collinearity. The centroid \( G \) bisects the line segment joining the orthocenter \( H \) and the circumcenter \( S \) in a \( 2:1 \) ratio, with \( HG \) being twice as long as \( GS \).

In the figure, triangle \( AGH \) is similar to triangle \( SGL \) by the Angle-Angle (AA) similarity criterion, as they share an angle at \( G \) and both have a right angle by the definition of altitude and perpendicular bisector, respectively.

The ratios of the corresponding sides of similar triangles \( AGH \) and \( SGL \) are equal to the ratio of their respective sides. If \( AG \), \( GH \), and \( GL \) are the lengths of the sides in \( AGH \), and \( SG \), \( GL \), and \( LS \) are the lengths of the sides in \( SGL \), then the ratios are:

\[ \frac{AG}{GL} = \frac{HG}{GS} = \frac{AH}{SL} \]

Given that \( G \) is the centroid, it divides the medians in a \( 2:1 \) ratio, so if we let the entire median from \( A \) to \( L \) be \( 3x \), then \( AG = 2x \) and \( GL = x \). This further defines the ratio of \( GH \) to \( SG \) as \( 2:1 \). The other sides will have a ratio that maintains this proportionality.

Given the centroid \( G \) of a triangle \( ABC \) expressed in terms of the orthocenter \( H \) and the circumcenter \( S \):

\[ G = \frac{2S + H}{3} \]

\[ H = 3G - 2S \]

\[ S = \frac{3G - H}{2} \]

These expressions allow us to interchangeably use the coordinates or positions of \( G \), \( H \), and \( S \) based on the centroid equation. These formulae are pretty useful when we know two of the centres and we wish to find the third one.

A very useful case

If the circumcenter \( S \) of a triangle is at the origin, then its coordinates are \( (0,0) \). Given the centroid formula \( G = \frac{2S + H}{3} \), and substituting \( S \) with the origin, we have:

[ G = \frac{2(0,0) + H}{3} ] [ G = \frac{H}{3} ]

Solving for \( H \), we get:

\[ H = 3G \]

Thus, when the circumcenter is at the origin, the orthocenter \( H \) is three times the vector of the centroid \( G \).

For a triangle \( ABC \) with vertices at \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \), and if the circumcenter \( S \) is at the origin \( (0,0) \), then the coordinates of the centroid \( G \) are given by:

\[ G\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right) \]

Now, using the formula \( H = 3G \) when \( S \) is at the origin, the coordinates of the orthocenter \( H \) are:

\[ H\left(3 \cdot \frac{x_1 + x_2 + x_3}{3}, 3 \cdot \frac{y_1 + y_2 + y_3}{3}\right) \]

Simplifying this, we get:

\[ H(x_1 + x_2 + x_3, y_1 + y_2 + y_3) \]

This formula represents the orthocenter \( H \) in terms of the coordinates of the vertices of triangle \( ABC \) when the circumcenter is at the origin.

Equilateral triangle and its centres

In an equilateral triangle \( ABC \) with vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \), the incenter, centroid, circumcenter, and orthocenter all coincide at the same point due to the symmetry of the triangle. The common point, often referred to as the triangle's center, can be found using the formula for the centroid which applies to all these centers in the case of an equilateral triangle:

\[ \left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right) \]

This point is equidistant from all the vertices and also equidistant from all the sides of the equilateral triangle. It serves as the center for the inscribed circle (incircle), the circumscribed circle (circumcircle), and is also the point where the altitudes, which are the same as the medians and the angle bisectors, intersect.

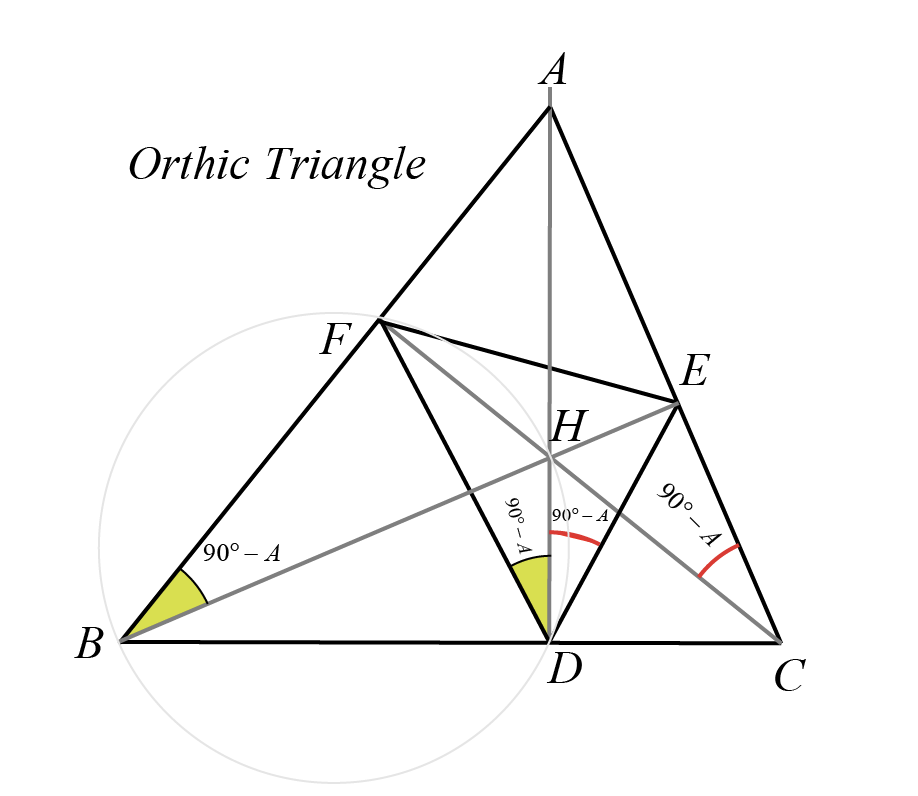
An important fact on Orthic Triangle

The orthic triangle \( DEF \) of the reference triangle \( ABC \) is formed by connecting the feet of the altitudes from each vertex of \( ABC \) to the opposite sides. In triangle \( ABC \), the points \( D \), \( E \), and \( F \) are the feet of the perpendiculars from vertices \( A \), \( B \), and \( C \), respectively.

In the orthic triangle \( DEF \), the incenter (the center of the inscribed circle) coincides with the orthocenter of the original triangle \( ABC \). This is because the altitudes of \( ABC \) are the angle bisectors of the orthic triangle \( DEF \). Since the incenter is the point where the angle bisectors of a triangle meet, the incenter of the orthic triangle \( DEF \) is indeed the point where the altitudes of triangle \( ABC \) intersect, which is the orthocenter of \( ABC \).

Explanation:

In triangle \( ABC \), \( DEF \) is the orthic triangle. \( FBDH \) is a cyclic quadrilateral because \( \angle BFH + \angle BDH = 180^\circ \) as both are right angles. Thus, there is a unique circle passing through all vertices of the quadrilateral. The angle subtended by chord \( FH \) at \( B \) is \( 90^\circ - A \) (as triangle \( ABE \) is right-angled at \( E \)). Then, the angle subtended by \( FH \) at \( D \) is also \( 90^\circ - A \). Similarly, \( HDCE \) is a cyclic quadrilateral; side \( HE \) subtends equal angles at \( D \) and \( C \), which is again \( 90^\circ - A \). Thus, \( \angle HDF = \angle HDE \) implying that \( AD \) is the angle bisector of \( \angle FDE \). Similarly, altitude \( BE \) is the angle bisector of \( \angle DEF \) and \( FC \) of \( \angle DFE \). Thus, the orthocenter of \( ABC \) is the incenter of the orthic triangle \( DEF \).