Concept of Sets, Notation and Operation

Why should one learn about Sets?

Sets serve as a foundational concept in mathematics, providing a framework for understanding and formalizing the notion of collections of objects. Knowledge of set theory is crucial because it forms the basis for various branches of mathematics, including algebra, geometry, and calculus.

For instance, consider the equation:

\[ (x(x - 1)(x - 2)(x - 3)(x - 4))^2 + ((x - 3)(x - 4)(x - 5))^2 = 0. \]

To find all real values of \( x \) that satisfy this equation, we apply the principle that if \( p^2 + q^2 = 0 \), then both \( p \) and \( q \) must be zero because the square of a real number is non-negative. Consequently, each term must independently equal zero.

Term 1: \( (x(x - 1)(x - 2)(x - 3)(x - 4))^2 = 0 \) yields solutions \( 0, 1, 2, 3, 4 \).

Term 2: \( ((x - 3)(x - 4)(x - 5))^2 = 0 \) yields solutions \( 3, 4, 5 \).

The comprehensive list of possible solutions is \( 0, 1, 2, 3, 4, 5 \) when combining all solutions. However, not all these values are actual solutions to the original equation; only \( x = 3 \) and \( x = 4 \) satisfy both terms simultaneously, thus making the entire expression equal to zero.

Using set theory, we can concisely express these findings. Let \( A = \{0, 1, 2, 3, 4\} \) represent the solutions from the first term, and \( B = \{3, 4, 5\} \) for the second term. The set containing all the potential solutions is \( A \cup B \), which is \( \{0, 1, 2, 3, 4, 5\} \). Nevertheless, the actual solution set, corresponding to values that satisfy both terms, is \( A \cap B = \{3, 4\} \). This illustrates the power of set theory in providing clear and succinct representations of complex concepts, highlighting its importance in mathematical problem-solving.

Definition of a Set

A set is an unordered collection of distinct, well-defined objects.

Unordered: The elements of a set do not have a specific sequence; their arrangement within the set does not matter. For example, if we consider a bag filled with colored balls, the order in which the balls are placed in the bag is irrelevant. Whether a red ball is added before a blue ball or vice versa, it does not change the contents of the bag.

Distinct: Sets contain unique elements, with no repetitions. Continuing with the bag analogy, even if we place several balls of the same color into the bag, within the context of set theory, we only acknowledge the presence of one ball of each color. If we were to list the contents, we would mention each color only once.

Well-Defined: The elements of a set must be clearly defined, allowing for unambiguous determination of whether an object belongs to the set or not. In terms of the bag analogy, this would be akin to having a rule that states only balls of certain colors can be included. If a ball's color is on the accepted list, it belongs in the bag; if not, it does not. This rule precisely determines the composition of the bag's contents.

An object in a set is referred to as an element or member of the set.

Set Notation

In set notation, sets are usually denoted by capital letters, and when there is a series of related sets, subscripts are employed to differentiate them. For example, \( A_1, A_2, A_3, \ldots \) might represent different sets in a sequence.

The curly braces \( \{ \} \) signify the collection of elements that constitute the set. These elements are written between the braces, separated by commas, and can include numbers, variables, or other types of objects.

Here are some examples of sets:

1. \( A = \{1, 2, 3, 4, 5, 6, 7\} \) is a set containing the first seven natural numbers.

2. \( B_{\text{odd}} = \{1, 3, 5, 7, 9\} \) represents a set of the first five odd numbers.

3. \( C_{\text{prime}} = \{2, 3, 5, 7, 11, 13, 17, 19, 23, \ldots\} \) represents the set of all prime numbers, which is infinite.

4. \( D_i = \{0, i, 2i, 3i, 4i\} \) where \( i \) is an integer and the set consists of the first five non-negative multiples of \( i \).

5. \( E_{\text{vowels}} = \{'a', 'e', 'i', 'o', 'u'\} \) is the set of lowercase vowels in the English alphabet.

Types of sets

• Null Set (Void Set or Empty Set): This is a set that contains no elements. It is denoted by \( \emptyset \) or \( \{\} \). The empty set is a subset of every set, including itself.

• Singleton Set: A singleton set contains exactly one element. For example, the set \( \{a\} \) is a singleton set because it contains only the element \( a \).

• Finite Set: A set is finite if it contains a limited number of elements. The number of elements in a finite set is a non-negative integer. For example, the set \( \{1, 2, 3, 4, 5\} \) is finite because it contains five elements.

• Infinite Set: A set is infinite if it contains an unlimited number of elements. In other words, an infinite set is not finite. The set of all natural numbers \( \mathbb{N} = \{1, 2, 3, \ldots\} \) is an example of an infinite set, as there is no limit to the counting numbers.

Special Symbols for some sets

Special sets in mathematics often represent collections of numbers with specific properties. YOu will be using this set throughout this course in every chapter.Here are descriptions of some of these sets:

1. \(\mathbb{R}\): Represents the set of all real numbers, which includes all rational and irrational numbers. Real numbers can be thought of as any point along an infinitely long line. This set encompasses all possible magnitudes and includes both positive and negative numbers, as well as zero.

2. \(\mathbb{Z}\): Denotes the set of all integers. Integers include all whole numbers and their negative counterparts, as well as zero. This set does not include fractions or decimal numbers.

3. \(\mathbb{N}\): Stands for the set of all natural numbers. Traditionally, natural numbers are the set of positive integers starting from 1, used for counting and ordering. Some definitions include zero in this set.

4. \(\mathbb{Q}\): Represents the set of all rational numbers. A rational number can be expressed as the quotient or fraction \(\frac{p}{q}\) of two integers, where \(p\) is the numerator, \(q\) is the denominator, and \(q \neq 0\). This set includes numbers such as \(\frac{1}{2}\), \(3\), and \(-\frac{4}{5}\).

5. \(\mathbb{W}\): Sometimes used to denote the set of whole numbers, though this notation is not as standardized as others. Whole numbers are similar to natural numbers but include zero, i.e., \(\{0, 1, 2, 3, \ldots\}\).

6. \(\mathbb{R} - \mathbb{Q}\): Represents the set of irrational numbers, which are real numbers that cannot be expressed as a ratio of two integers. These numbers have non-repeating, non-terminating decimal expansions. Examples include \(\sqrt{2}\) and \(\pi\).

7. \(\mathbb{R}^+\): Denotes the set of all positive real numbers. This set includes all real numbers greater than zero, covering both rational and irrational numbers, but excludes zero itself.

8. \(\mathbb{Z}^+\): Represents the set of all positive integers, also known as the set of natural numbers by some definitions. This includes numbers like \(1, 2, 3, \ldots\), excluding zero and any negative numbers.

These sets play crucial roles in various branches of mathematics, providing a foundation for defining numbers, operations, and mathematical concepts.

Set Membership Symbol

The set membership symbol \( \in \) denotes "is a member of" or "is an element of." Conversely, the symbol \( \notin \) indicates "does not belong to" or "is not an element of."

For example, using the set of prime numbers \( P = \{2, 3, 5, 7, 11, \ldots\} \):

• \( 3 \in P \) means 3 is a member of the set of prime numbers.
• \( 4 \notin P \) means 4 is not a member of the set of prime numbers.

Subset and Superset

Subset

A subset is defined as follows: Given two sets \( A \) and \( B \), if every element of set \( A \) is also an element of set \( B \), then \( A \) is a subset of \( B \), denoted as \( A \subseteq B \).

For example, consider the set of prime numbers less than 10, \( P = \{2, 3, 5, 7\} \), and the set of natural numbers \( \mathbb{N} = \{1, 2, 3, 4, 5, \ldots\} \). Since every element of \( P \) is also an element of \( \mathbb{N} \), we can say that \( P \) is a subset of \( \mathbb{N} \), or \( P \subseteq \mathbb{N} \).

Superset

A superset is defined in relation to the concept of a subset. Given two sets \( A \) and \( B \), if every element of \( A \) is also an element of \( B \), then \( A \) is a subset of \( B \), denoted as \( A \subseteq B \). Conversely, \( B \) is said to be a superset of \( A \), which means that \( B \) contains all elements of \( A \) along with possibly more elements not in \( A \). The notation for \( B \) being a superset of \( A \) is \( B \supseteq A \).

How to prove a set is subset of another set

To prove theoretically that a set \( A \) is a subset of another set \( B \), one typically follows these steps:

1. Assume an Arbitrary Element: Take an arbitrary element \( x \) from set \( A \). The choice of \( x \) is arbitrary to ensure that the argument applies to every element of \( A \) without exception.

2. Demonstrate Membership in \( B \): Then, using definitions, properties, or other logical arguments, demonstrate that this arbitrary element \( x \) also belongs to set \( B \), i.e., show that \( x \in B \).

3. Apply Universal Generalization: Since the element \( x \) was chosen arbitrarily from \( A \) and it was shown that \( x \in B \), by the principle of universal generalization, one can conclude that this argument holds for all elements of \( A \). Therefore, every element of \( A \) is also an element of \( B \), which means \( A \subseteq B \).

This method relies on the foundational logic that if a property holds for any arbitrary element of a set, then it holds for all elements of that set.

The empty set, denoted by \( \emptyset \), is indeed a subset of any set. This is because the statement that "every element of the empty set is also an element of any given set" is vacuously true, as the empty set contains no elements to contradict this statement. Thus, by definition, \( \emptyset \subseteq A \) for any set \( A \).

Similarly, any set \( A \) is a subset of itself, expressed as \( A \subseteq A \). This is because every element in \( A \) is, by definition, an element of \( A \), satisfying the criterion for being a subset.

Equality of Sets

Equality of two sets occurs when they contain exactly the same elements. A more precise definition is that two sets \( A \) and \( B \) are equal, denoted as \( A = B \), if every element of \( A \) is in \( B \) and every element of \( B \) is in \( A \). This condition implies that \( A \) is a subset of \( B \) (\( A \subseteq B \)) and \( B \) is a subset of \( A \) (\( B \subseteq A \)). The mutual subset relationship establishes that \( A \) and \( B \) have identical membership, hence are equal.

Let's consider two sets \( A = \{1, 2, 3\} \) and \( B = \{3, 2, 1\} \).

To demonstrate \( A = B \):

1. Show \( A \subseteq B \): Every element of \( A \) (which are 1, 2, and 3) is also found in \( B \). There is no element in \( A \) that is not in \( B \).

2. Show \( B \subseteq A \): Similarly, every element of \( B \) (which are 3, 2, and 1, noting the order does not matter in a set) is also found in \( A \). There is no element in \( B \) that is not in \( A \).

Since both \( A \subseteq B \) and \( B \subseteq A \) are true, by definition, \( A = B \). This demonstrates that despite the difference in how the elements are listed, the sets are equal because they contain the exact same elements.

Proper Subset

A proper subset is defined when set \( A \) is a subset of set \( B \), and there exists at least one element in \( B \) that is not in \( A \). This relationship is denoted as \( A \subsetneq B \) or simply \( A \subset B \), indicating that while all elements of \( A \) are in \( B \), \( A \) does not contain every element of \( B \), making \( A \) strictly smaller than \( B \) in terms of its composition. The distinction here is that \( A \) cannot be equal to \( B \); there must be at least one element that is unique to \( B \), which is not found in \( A \).

Let \( A = \{1, 2\} \) and \( B = \{1, 2, 3\} \).

In this case, \( A \) is a proper subset of \( B \) because:

• Every element of \( A \) (which are 1 and 2) is also in \( B \).
• There is at least one element in \( B \) (which is 3) that is not in \( A \).

Thus, \( A \subsetneq B \) or \( A \subset B \), demonstrating that \( A \) is a proper subset of \( B \).

Operations on Sets

Union

The union of two sets \( A \) and \( B \), denoted by \( A \cup B \), is the process of merging the elements of \( A \) and \( B \) into a single set where each distinct element appears only once. This operation does not consider the repetition of elements; if an element is present in both \( A \) and \( B \), it is included only once in the union.

Precisely defined, the union \( A \cup B \) can be represented as:

\[ A \cup B = \{x : x \in A \text{ or } x \in B\} \]

This means the set \( A \cup B \) consists of all elements \( x \) such that \( x \) is an element of \( A \), an element of \( B \), or an element of both.

Example

Let \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \).

The union \( A \cup B \) is:

\[ A \cup B = \{1, 2, 3, 4, 5\} \]

This set contains all distinct elements from both \( A \) and \( B \), with the element \( 3 \), which is common to both sets, included only once.

Intersection of two sets

The intersection of two sets \( A \) and \( B \), denoted by \( A \cap B \), is defined as the set containing all elements that are common to both \( A \) and \( B \). In other words, an element \( x \) is in \( A \cap B \) if and only if \( x \) is in both \( A \) and \( B \).

Formally, the intersection is represented as:

\[ A \cap B = \{x : x \in A \text{ and } x \in B\} \]

This definition implies that for an element to be included in the intersection set, it must satisfy the membership criteria for both of the original sets.

Example

I. Let \( A = \{1, 2, 3, 4\} \) and \( B = \{3, 4, 5, 6\} \).

The intersection \( A \cap B \) is:

\[ A \cap B = \{3, 4\} \]

These are the elements common to both sets \( A \) and \( B \).

II. The intersection of the set of integers \( \mathbb{Z} \) and the set of natural numbers \( \mathbb{N} \) is the set of all natural numbers, since natural numbers are a subset of integers that includes all positive integers starting from 1 (assuming the definition of \( \mathbb{N} \) does not include 0). Thus,

\[ \mathbb{Z} \cap \mathbb{N} = \mathbb{N} \]

This includes all positive integers \( \{1, 2, 3, 4, \ldots\} \).

The intersection of two sets can indeed be the null set, also known as the empty set \( \emptyset \), when the two sets have no elements in common. Sets with this property are referred to as disjoint sets.

Formally, two sets \( A \) and \( B \) are disjoint if their intersection is the empty set:

\[ A \cap B = \emptyset \]

This means there are no elements that both \( A \) and \( B \) share.

Universal Set

The universal set, typically denoted by \( U \), is the set that contains all objects or elements under consideration for a particular discussion or problem. Every other set within the context of that discussion is a subset of the universal set. The concept of a universal set is relative to the scope of the discussion; what constitutes \( U \) in one context may differ in another.

For example, if the discussion is limited to numbers involved in a certain mathematical problem, the universal set might consist of just those numbers. In a discussion about geometric shapes, the universal set would include all the shapes under consideration.

The universal set serves as a reference for operations like complementation, where the complement of a set \( A \) within \( U \) includes all elements in \( U \) that are not in \( A \).

Example

In a class students have preferences for either Mythology or Philosophy, the universal set \( U \) can be defined as the complete list of these students.

Let's consider the universal set \( U \) to be:

\[ U = \{\text{Zeus, Hera, Athena, Apollo, Artemis}\} \]

We define two subsets of \( U \):

• \( A \) for students who like Mythology.
• \( B \) for students who like Philosophy.

If Zeus, Athena, and Apollo like Mythology, and Athena and Artemis like Philosophy, then the sets can be represented as:

• \( A = \{\text{Zeus, Athena, Apollo}\} \)
• \( B = \{\text{Athena, Artemis}\} \)

In this context:

• The universal set \( U \) represents all students in the class.
• \( A \) and \( B \) are subsets of \( U \), where \( A \) includes the students interested in Mythology and \( B \) those interested in Philosophy. Athena, having an interest in both subjects, is included in both subsets \( A \) and \( B \).

Complement of a Set

The complement of a set \( A \), denoted by \( A^c \) (or sometimes \( \bar{A} \)), consists of all elements that are in the universal set \( U \) but not in \( A \). The concept of the complement relies on the existence of a universal set \( U \), which contains all objects or elements under consideration.

Formally, the complement of \( A \) is defined as:

\[ A^c = \{x \in U : x \notin A\} \]

This means that \( A^c \) includes every element that is part of \( U \) but is excluded from \( A \). It's important to note that the complement of \( A \) is relative to \( U \); changing \( U \) can change \( A^c \).

Example

Let's consider a universal set \( U \) that represents all the letters in the English alphabet:

\[ U = \{A, B, C, D, \ldots, Z\} \]

Now, define set \( A \) as the set of vowels in the English alphabet:

\[ A = \{A, E, I, O, U\} \]

The complement of set \( A \), denoted as \( A^c \), includes all the letters in the English alphabet that are not vowels, which means all the consonants. Therefore, \( A^c \) is:

\[ A^c = \{B, C, D, F, G, H, J, K, L, M, N, P, Q, R, S, T, V, W, X, Y, Z\} \]

Here, \( A^c \) represents all elements of the universal set \( U \) that are not in \( A \), showcasing that the complement set consists of all the consonants.

Example

In the context where the universal set \( U \) is the set of all real numbers \( \mathbb{R} \), and considering \( \mathbb{Q} \) as the set of all rational numbers, the complement of \( \mathbb{Q} \) in \( \mathbb{R} \), denoted as \( \mathbb{Q}^c \), would consist of all irrational numbers.

Thus, \( \mathbb{Q}^c \) is:

\[ \mathbb{Q}^c = \{x \in \mathbb{R} : x \notin \mathbb{Q}\} \]

This includes numbers such as \( \sqrt{2} \), \( \pi \), \( e \), and any other real number that cannot be expressed as a ratio of two integers.

Set Difference

The difference of two sets \( A \) and \( B \), denoted by \( A - B \) or \( A \setminus B \), consists of all elements that are in \( A \) but not in \( B \). This operation effectively "subtracts" the elements of \( B \) from \( A \).

Formally, the difference is defined as:

\[ A - B = \{x : x \in A \text{ and } x \notin B\} \]

This means that \( A - B \) includes every element that is a member of \( A \) but excludes any member that is also in \( B \). The difference of sets highlights the elements that are unique to the first set when compared to the second.

Example

Let \( A = \{1, 2, 3, 4, 5\} \) and \( B = \{4, 5, 6, 7\} \).

The difference \( A - B \) is:

\[ A - B = \{1, 2, 3\} \]

This set includes all the elements that are in \( A \) but not in \( B \), which are \( 1 \), \( 2 \), and \( 3 \).

Also,

The difference \( B - A \) is calculated as:

\[ B - A = \{6, 7\} \]

This represents the elements that are unique to \( B \) when the elements of \( A \) are removed, specifically \( 6 \) and \( 7 \).

Example

Given the universal set of real numbers \( \mathbb{R} \) and the set of rational numbers \( \mathbb{Q} \),

• \( \mathbb{R} - \mathbb{Q} \) represents the set of all irrational numbers, which are real numbers that cannot be expressed as the ratio of two integers. Examples include \( \sqrt{2} \), \( \pi \), and \( e \).

• \( \mathbb{Q} - \mathbb{R} \) is a theoretical expression that doesn't practically apply because \( \mathbb{Q} \) is a subset of \( \mathbb{R} \). Since all rational numbers are already within the real numbers, \( \mathbb{Q} - \mathbb{R} \) would result in the empty set \( \emptyset \), as there are no elements in \( \mathbb{Q} \) that are not in \( \mathbb{R} \).

Intervals

A brief history of real numbers

The history of numbers encompasses the evolution from counting numbers (natural numbers \(\mathbb{N}\)) to a more comprehensive understanding that includes whole numbers, fractions (rational numbers \(\mathbb{Q}\)), and the realization of irrational numbers. Initially, natural numbers (\(1, 2, 3, \ldots\)) were used for counting. The concept of zero was later introduced, expanding the set to whole numbers (\(0, 1, 2, 3, \ldots\)). Fractions led to the development of rational numbers, which can be expressed as the quotient \(\frac{a}{b}\), where \(a\) and \(b\) are integers, and \(b \neq 0\).

The Greeks, using ropes to measure lengths, could represent any rational number. For instance, if a rope is one unit long and divided into three parts, then two parts represent \(\frac{2}{3}\). However, the discovery that not all numbers are rational marked a significant advancement in mathematics. It was Hippasus of the Pythagorean school who first suggested that the square root of 2 (\(\sqrt{2}\)) could not be expressed as a fraction, implying its irrationality. He did that by showing that the diagonal of a square with side length 1 unit cannot be expressed as a rational number, though it clearly exists as a geometric length. This was a shocking revelation, as it contradicted the Pythagorean belief in the universality of rational numbers.

The formal proof of the irrationality of \(\sqrt{2}\) is due to Euclid, who showed that if \(\sqrt{2}\) were rational, it would lead to a contradiction, thereby establishing its irrational nature. This proof is a milestone in the history of mathematics, highlighting the existence of numbers beyond the rational spectrum, and leading to the broader concept of real numbers (\(\mathbb{R}\)), which includes both rational and irrational numbers.

Thus, the set of rational numbers (\(\mathbb{Q}\)) has "gaps," which are points on the number line that cannot be represented by any rational number. These gaps correspond to irrational numbers—numbers that cannot be expressed as the ratio of two integers. The existence of these gaps highlights the incompleteness of the rational numbers as a number system when compared to the real numbers (\(\mathbb{R}\)).

The real numbers include both rational numbers and irrational numbers, thereby "completing" the number line without gaps. This completeness is a fundamental property of the real numbers, essential for the development of calculus, analysis, and much of modern mathematics.

In foundational mathematics, real numbers are often introduced through intuitive concepts or as an axiom set, especially at elementary levels, allowing for an immediate application in calculus and analysis. However, in higher mathematics, the construction and properties of real numbers are treated with rigorous formalism, based on set theory and axiomatic frameworks.

In the higher mathematics framework, particularly in real analysis, the real numbers (\(\mathbb{R}\)) are constructed and understood through rigorous axiomatic approaches. Beyond considering real numbers as an intuitive or axiomatic set, advanced mathematical treatments often involve principles like the Nested Interval Property (NIP), and the Axiom of Completeness, to systematically construct and analyze real numbers. One foundational approach to constructing the real numbers (\(\mathbb{R}\)) is through the completion of the rational numbers (\(\mathbb{Q}\)), using techniques like Dedekind cuts or Cauchy sequences.

Negative Numbers

Negative numbers were initially met with skepticism due to their abstract nature. Their early use can be traced back to ancient China and India, where they were used for practical purposes like accounting and solving equations. Chinese mathematicians during the Han Dynasty and Indian mathematicians like Brahmagupta in the 7th century AD were among the first to formally recognize and use negative numbers.

In Europe, the acceptance of negative numbers evolved slowly, gaining traction in the 15th and 16th centuries with their utility in solving quadratic equations and bookkeeping. It wasn't until the 17th century, with mathematicians such as John Wallis and Isaac Newton, and the advent of coordinate geometry by René Descartes, that negative numbers became widely accepted. By the 18th and 19th centuries, with the formalization of mathematical concepts, negative numbers were fully integrated into mathematics, becoming indispensable across various fields.

Definition of an Interval

An interval is a set of real numbers lying between two specific real numbers, serving as the set's endpoints. This concept closely parallels the geometric idea of segments or cuts on the real line, where an interval represents a continuous stretch or segment between two points on this line. Just as a segment in geometry connects two points on a plane or in space, an interval connects two points on the number line, encompassing all the real numbers that lie between these two points.

Why is an interval a set?

An interval is a set because it meets the definition of a set: a collection of distinct objects considered as a whole. In the context of intervals within the real numbers, these "objects" are the real numbers that fall within specified boundaries (endpoints). Like any set, an interval can be described by its members' properties, specifically those real numbers that lie between its endpoints, whether or not including the endpoints themselves. This collection of numbers, defined by a common property of lying within certain bounds on the real number line, thus forms a set according to the principles of set theory.

Closed Interval

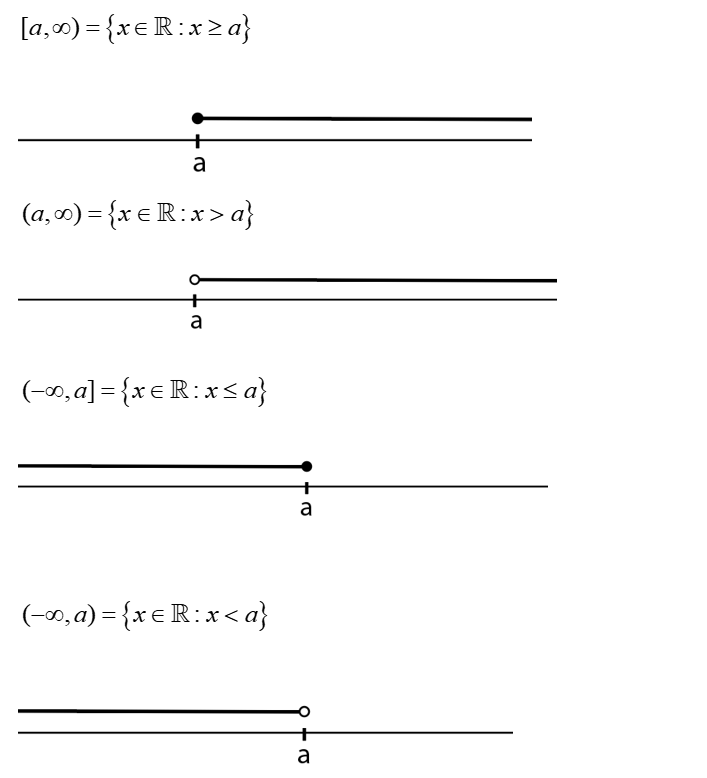
A closed interval is a set of real numbers that includes all the numbers between two specified endpoints, and importantly, it also includes the endpoints themselves. If \(a\) and \(b\) are the endpoints, the closed interval is denoted by \([a, b]\), where \(a \leq x \leq b\) for any \(x\) in the interval. This means every number greater than or equal to \(a\) and less than or equal to \(b\) is part of the interval, making it "closed" because it contains its boundary points.

A closed interval \([a, b]\) can be written in set-builder form as:

\[ \{x \in \mathbb{R} \mid a \leq x \leq b\} \]

This denotes the set of all real numbers \(x\) such that \(x\) is greater than or equal to \(a\) and less than or equal to \(b\).

This visual representation depicts a closed interval on the real number line. The darkened horizontal line between the points labeled \( a \) and \( b \) represents all the real numbers that are included in the interval. The filled-in circles at \( a \) and \( b \) indicate that these endpoint values are included in the interval. The closed interval includes all real numbers from \( a \) to \( b \), inclusive of the endpoints. This interval is mathematically denoted as \([a, b]\).

Open Interval

An open interval is a set of real numbers that includes all the numbers between two specified endpoints but does not include the endpoints themselves. If \( a \) and \( b \) are the endpoints, the open interval is denoted by \( (a, b) \), where \( a < x < b \) for any \( x \) in the interval. This means every number that is strictly greater than \( a \) and strictly less than \( b \) is part of the interval, making it "open" because it excludes its boundary points. In set-builder notation, an open interval is written as:

\[ \{ x \in \mathbb{R} \mid a < x < b \} \]

This denotes the set of all real numbers \( x \) such that \( x \) is greater than \( a \) and less than \( b \), without including \( a \) and \( b \) themselves.

This diagram represents an open interval on the real number line. The line segment between the points labeled \( a \) and \( b \) symbolizes all the real numbers that lie between \( a \) and \( b \). The open circles at \( a \) and \( b \) illustrate that these endpoint values are not included in the interval. Mathematically, this open interval is denoted as \( (a, b) \), encompassing all real numbers greater than \( a \) and less than \( b \), but excluding the endpoints \( a \) and \( b \) themselves.

Maximum and Minimum of a set

The maximum of a set is an element belonging to the set such that it is greater than or equal to every other element in the set. Conversely, the minimum of a set is an element belonging to the set such that it is less than or equal to every other element in the set.

For the set \( \{1, 2, 3, 4, 5\} \):

• The maximum is 5, because it is the element in the set that is greater than or equal to all other elements.
• The minimum is 1, because it is the element in the set that is less than or equal to all other elements.

An important difference between closed and open intervals

For the closed interval \([-2, 3]\):

• The maximum is 3, because 3 is included in the interval and there is no other number in the interval that is greater than 3.
• The minimum is -2, because -2 is included in the interval and there is no other number in the interval that is less than -2.

Since the interval is closed, both endpoints -2 and 3 are included in the interval, and they serve as the minimum and maximum, respectively.

For the open interval \((-2, 3)\):

• The maximum does not exist because, although numbers in the interval can get arbitrarily close to 3, there is no largest number since 3 itself is not included.
• Similarly, the minimum does not exist because numbers can get arbitrarily close to -2 from above, but -2 is not an element of the interval.

In the open interval, for any number you choose that you might think is the greatest, you can always find another number closer to 3 but still not equal to 3. This means there is no "last" number before 3, so no maximum exists in the set. The same reasoning applies for not having a minimum value in the set. The numbers can always get closer to -2 from the right without ever reaching -2, so there is no "first" number after -2. For example:

\[ 2.9 < 2.99 < 2.999 < 2.9999 < \ldots \]

This sequence can continue indefinitely with more 9s being added, getting increasingly closer to 3, but never actually reaching 3. Since the interval is open, 3 itself is not included, and hence, we can never actually arrive at the maximum. Similarly, approaching the lower bound, we find:

\[ -1.9 > -1.99 > -1.999 > -1.9999 > \ldots \]

This shows how you can always choose a number closer to -2 from the right, yet never include -2 itself, thus the interval does not have a minimum either.

In general, a closed interval includes its endpoints, meaning it has both a maximum and a minimum element. An open interval, on the other hand, does not include its endpoints, and therefore does not have a maximum or a minimum element.

Semi-closed Interval

A semi-closed interval, or half-open interval, is an interval that includes one of its endpoints but leaves the other endpoint excluded. This leads to two main types of semi-closed intervals:

1. Left-Closed, Right-Open Interval \([a, b)\): This type includes the left endpoint \(a\) but excludes the right endpoint \(b\), covering all real numbers \(x\) where \(a \leq x < b\). The inclusion of \(a\) is indicated by a square bracket, while the exclusion of \(b\) is denoted by a parenthesis.

   Set-builder notation for this interval is \(\{x \in \mathbb{R} \mid a \leq x < b\}\).

   

2. Left-Open, Right-Closed Interval \((a, b]\): This interval excludes the left endpoint \(a\) but includes the right endpoint \(b\), and it consists of all real numbers \(x\) where \(a < x \leq b\).

   Set-builder notation for this interval is \(\{x \in \mathbb{R} \mid a < x \leq b\}\).

   

When involving infinity, semi-closed intervals extend without a bound in one direction, which impacts the existence of a maximum or minimum:

• Extending to Positive Infinity \([a, \infty)\): Includes all real numbers \(x\) greater than or equal to \(a\) and extends without limit towards positive infinity. Here, the interval includes its left endpoint \(a\), but since it extends towards infinity, there is no maximum value, reflecting the interval's open nature on the right.

  Set-builder notation: \(\{x \in \mathbb{R} \mid x \geq a\}\).

• Extending to Negative Infinity \((-\infty, b]\): Includes all real numbers \(x\) less than or equal to \(b\) and extends without limit towards negative infinity. The interval includes its right endpoint \(b\), but due to its extension towards negative infinity, there is no minimum value, making the interval open on the left.

  Set-builder notation: \(\{x \in \mathbb{R} \mid x \leq b\}\).

In such intervals that extend towards infinity, the absence of a bound on one side means that there is no maximum (for intervals extending to positive infinity) or no minimum (for intervals extending to negative infinity), thus maintaining their open characteristic on the respective infinite end.

The interval \((- \infty, \infty)\) is equivalent to the set of all real numbers, \(\mathbb{R}\), representing the entire real number line without any bounds.

Degenerate Intervals

Degenerate intervals refer to intervals that consist of a single point or no points at all:

• The closed interval \([a, a]\) represents a degenerate interval that includes exactly one point, \(a\). This can be equivalently written as the singleton set \(\{a\}\), indicating that the interval spans no distance on the number line but contains the point \(a\).

• The open interval \((a, a)\) is another form of a degenerate interval, equivalent to the empty set \(\emptyset\). This interval spans no distance and includes no points, as the open nature excludes both endpoints, even though they are the same.

Operations on Intervals

Since intervals are sets, all standard set operations such as union, intersection, and difference are valid for intervals as well. These operations on intervals follow the same principles as they do for any other sets.

Union

The union of two intervals is a set that contains all the elements that are in either interval or in both. This operation combines the ranges covered by the intervals into a single set, which may consist of a single continuous interval or multiple disjoint intervals, depending on the overlap between the original intervals.

The union of two intervals results in either a single continuous interval or two disjoint intervals, depending on the relationship between the intervals:

1. Single Continuous Interval: The union forms a single continuous interval if the intervals overlap, directly meet at a boundary point, or one interval includes a boundary point that the other interval approaches but does not include. This encompasses cases where intervals share common elements or if the end of one interval coincides with the start of another, with at least one of the intervals including this common endpoint.

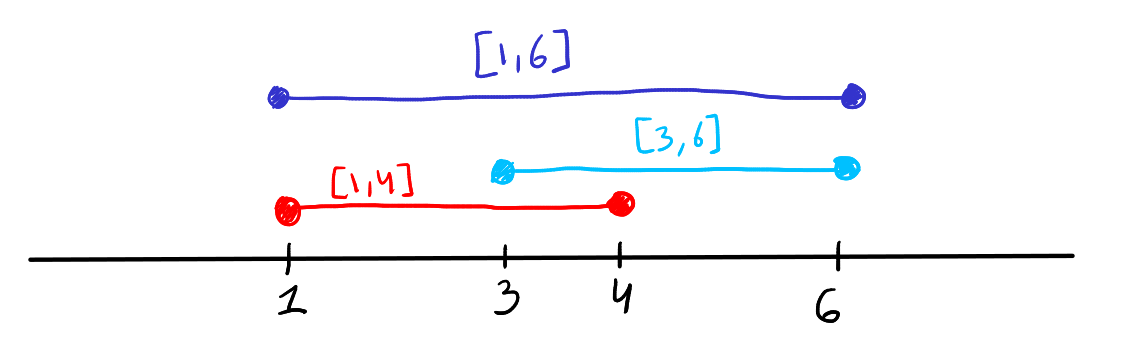
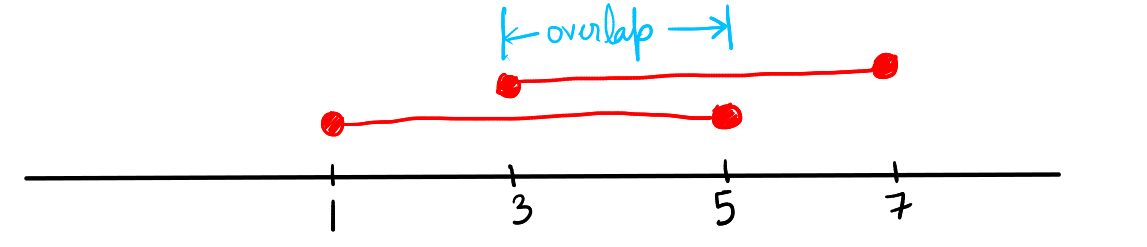
   • Overlap Example: For intervals \(A = [1, 4]\) and \(B = [3, 6]\), the union \(A \cup B = [1, 6]\) because they have ana overlap from 3 to 4, creating a single continuous interval from 1 to 6.

   

   • Meeting at a Boundary Example: For intervals \(A = (-1, 3)\) and \(B = [3, 7)\), although \(A\) does not include 3 and \(B\) does, the union \(A \cup B = (-1, 7)\) forms a single continuous interval because \(B\) includes the boundary point where \(A\) ends, bridging the potential gap.

   

2. Two Disjoint Intervals: The union results in two disjoint intervals if there's a gap between the intervals, meaning they neither overlap nor touch at any point. In this case, the union reflects a set comprising two separate intervals with no common elements.

   • Disjoint Example: For intervals \(A = [1, 2]\) and \(B = [3, 4]\), there's a clear gap between them. The union \(A \cup B\) cannot be simplified to a single interval due to the absence of shared or touching elements, resulting in two disjoint intervals: \([1, 2] \cup [3, 4]\).

     

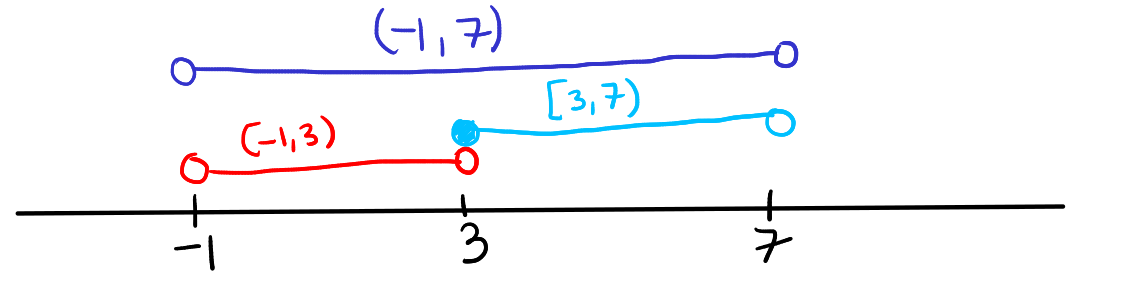
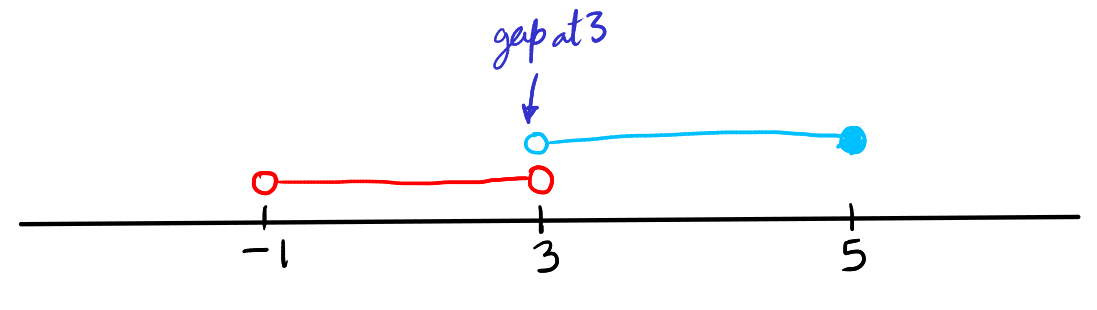
     Consider union of \( (-1, 3) \) and \( (3, 5] \). For the intervals \( (-1, 3) \) and \( (3, 5] \), both intervals approach the point 3 but neither includes it; \( (-1, 3) \) is open at 3, and \( (3, 5] \) is also open at 3. Since there is no shared endpoint included in either interval, they do not directly meet or overlap at any point. In this case, the union \( (-1, 3) \cup (3, 5] \) does not form a single continuous interval because there is no common element to connect them seamlessly. Instead, the union represents a set comprising two disjoint intervals: one stretching from -1 to just below 3, and the other from just above 3 to 5, inclusive of 5. So, despite their proximity, the absence of a shared, included boundary point keeps \( (-1, 3) \) and \( (3, 5] \) as distinct, separate intervals within their union.

     

In summary, whether the union of two intervals forms a single continuous interval or remains as two disjoint intervals hinges on their overlap or direct connection at a boundary point (with at least one interval including it) versus a complete separation without shared or adjacent points.

Example

A. \((- \infty, 1) \cup (0, 4] \cup (5, 8]\)

Solution:

The union \((- \infty, 1) \cup (0, 4] \cup (5, 8]\) forms two intervals: \((- \infty, 4]\) and \((5, 8]\), since the first two intervals overlap and combine into a single continuous interval, while the third interval remains separate due to a gap. The final answer is thus \((- \infty, 4] \cup (5, 8]\).

B. \((1, 3) \cup \{3\}\)

Solution:

The union \((1, 3) \cup \{3\}\) results in the interval \((1, 3]\), which includes all numbers greater than 1 and up to and including 3.

Intersection of Intervals

The intersection of intervals refers to the set of all elements that are common to both intervals. Mathematically, if there are two intervals \(A\) and \(B\), their intersection is denoted by \(A \cap B\), and it includes all points that lie within both \(A\) and \(B\). The result of an intersection can be:

• A non-empty interval, if \(A\) and \(B\) share a common range of points. This interval could be open, closed, or semi-closed, depending on the specific endpoints of \(A\) and \(B\) that fall within the intersection.
• An empty set, denoted by \(\emptyset\), if \(A\) and \(B\) do not share any points, indicating that there is no overlap between the two intervals. This is still considered an interval, albeit a degenerate one, as it represents the set of all real numbers that are in both intervals, of which there are none.

Examples

1. • Let \( A = [1, 5] \) and \( B = [3, 7] \).
   • The intersection \( A \cap B = [3, 5] \). This interval includes all points that are common to both \( A \) and \( B \), specifically the numbers from 3 to 5, inclusive.

   Example 1: Overlapping Closed Intervals

   

2. Example 2: One Open and One Closed Interval

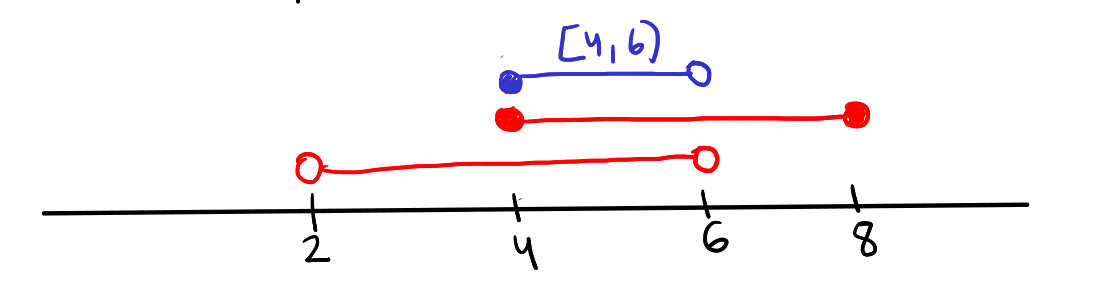
   • Let \( A = (2, 6) \) and \( B = [4, 8] \).
   • The intersection \( A \cap B = [4, 6) \). In this case, the intersection is closed at 4, because 4 lies in A as well as B, and it is open at 6 because 6 is not in A.

   

3. Example 3: Disjoint Intervals

   • Let \( A = [0, 2] \) and \( B = (3, 5) \).
   • The intersection \( A \cap B = \emptyset \). These intervals do not overlap; there are no points common to both \( A \) and \( B \), resulting in an empty intersection.

4. Example 4: Semi-Closed Intervals Touching at a Point

   • Let \( A = [1, 4) \) and \( B = (4, 6] \).
   • The intersection \( A \cap B = \emptyset \). Although \( A \) ends at 4 and \( B \) starts from 4, \( A \) does not include 4 and \( B \) is open at 4, so they have no points in common, resulting in an empty intersection.

5. Example 5: Nested Intervals

   • Let \( A = [1, 10] \) and \( B = [3, 8] \).
   • The intersection \( A \cap B = [3, 8] \). Here, \( B \) is entirely contained within \( A \), so their intersection is simply \( B \), the interval that lies completely within both intervals.

6. Example 6: The intersection of the intervals \((-1, 1]\) and \([1, 3)\) is the set \(\{1\}\), which is the point where the two intervals meet. Since one interval includes 1 and the other starts at 1, their intersection includes just this single point, making it a degenerate interval represented by the singleton set containing the element 1.

Difference of Intervals

The difference of two intervals \(A\) and \(B\), denoted as \(A - B\) or \(A \setminus B\), consists of all elements that are in \(A\) but not in \(B\). This operation effectively "subtracts" the elements of \(B\) from \(A\), and the result can vary widely depending on the specific intervals involved:

• It could result in a single interval if \(B\) only partially overlaps with \(A\) or does not overlap at all.
• It might produce two disjoint intervals if \(B\) is contained within \(A\), creating a gap in the middle of \(A\).
• The difference could also be an empty set if \(A\) is entirely contained within \(B\), meaning all elements of \(A\) are also in \(B\).

Examples

1. \(\mathbb{R} - (-1, 1) = (-\infty, -1] \cup [1, \infty)\)

   • Removing the open interval \((-1, 1)\) from the set of all real numbers (\(\mathbb{R}\)) excludes all numbers strictly between -1 and 1. The result is two disjoint intervals: \((- \infty, -1]\) includes every number up to and including -1 (closed at -1), and \([1, \infty)\) includes every number from 1 onwards but does not include 1 itself (open at 1).

2. \(\mathbb{R} - [-1, 1] = (-\infty, -1) \cup (1, \infty)\)

   • Subtracting the closed interval \([-1, 1]\) from \(\mathbb{R}\) removes all numbers from -1 to 1, inclusive of the endpoints. The intervals \((- \infty, -1)\) and \((1, \infty)\) are both open, meaning they do not include -1 and 1, respectively, reflecting that numbers as close as possible to -1 and 1 are included without including -1 and 1 themselves.

3. \(\mathbb{R} - (-1, 1] = (-\infty, -1] \cup (1, \infty)\)

   • Here, subtracting the semi-closed interval \((-1, 1]\) from \(\mathbb{R}\) excludes numbers greater than -1 up to and including 1. The result combines a closed interval \((- \infty, -1]\) with an open interval \((1, \infty)\), signifying inclusion of -1 but exclusion of 1 from the result.

4. \((-1, 1) - (0, \infty) = (-1, 0]\)

   • This operation subtracts all numbers greater than 0 from the open interval \((-1, 1)\), leaving only numbers from -1 up to and including 0. Since -1 is not included and 0 is, the result is a semi-closed interval \((-1, 0]\), which is open at -1 and closed at 0.

5. \(\mathbb{R} - \{3\} = (-\infty, 3) \cup (3, \infty)\)

   • Subtracting the singleton set \(\{3\}\) from the set of all real numbers leaves every number except 3. This results in two disjoint intervals: one stretching from negative infinity up to, but not including, 3, and another from just above 3 to positive infinity, effectively excluding only the number 3 from the real number line.

6. \((-1, 1) - \mathbb{R}=\emptyset\)

   • The operation \((-1, 1) - \mathbb{R}\) does not follow the typical context of set difference because subtracting all real numbers (\(\mathbb{R}\)) from any interval, including \((-1, 1)\), results in the empty set, denoted as \(\emptyset\). This is because \(\mathbb{R}\) contains all possible real numbers, including those in the interval \((-1, 1)\), and subtracting the entire set of real numbers from a subset of itself leaves nothing.