Quadratic Expressions
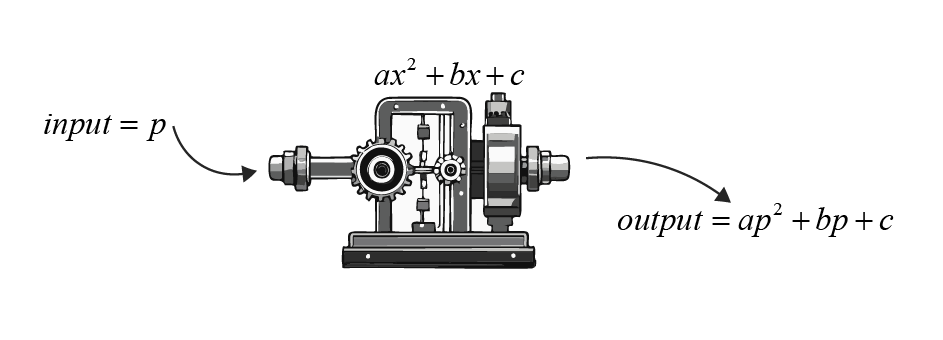
A quadratic expression is one of the simplest forms of a polynomial, characterized by an exponent of two as its highest power. Written in its most recognizable form, \( ax^2 + bx + c \), each of the constants—\( a \), \( b \), and \( c \)—play a specific role in shaping its graph. Here, \( a \) must be a non-zero number to ensure that the expression is indeed quadratic. \(x\) is the variable of the expression and it can be any real number.
Consider a quadratic expression as a machine where you put in a number for \( x \), and it gives you a number back. This is like feeding a number into a calculator programmed with the quadratic expression, and it displays the result. You put some input into it and it produces some output. When you put some value of \(x\), say \(p\) into it, it gives you the output \(ap^2+bp+c\).
Take an example.
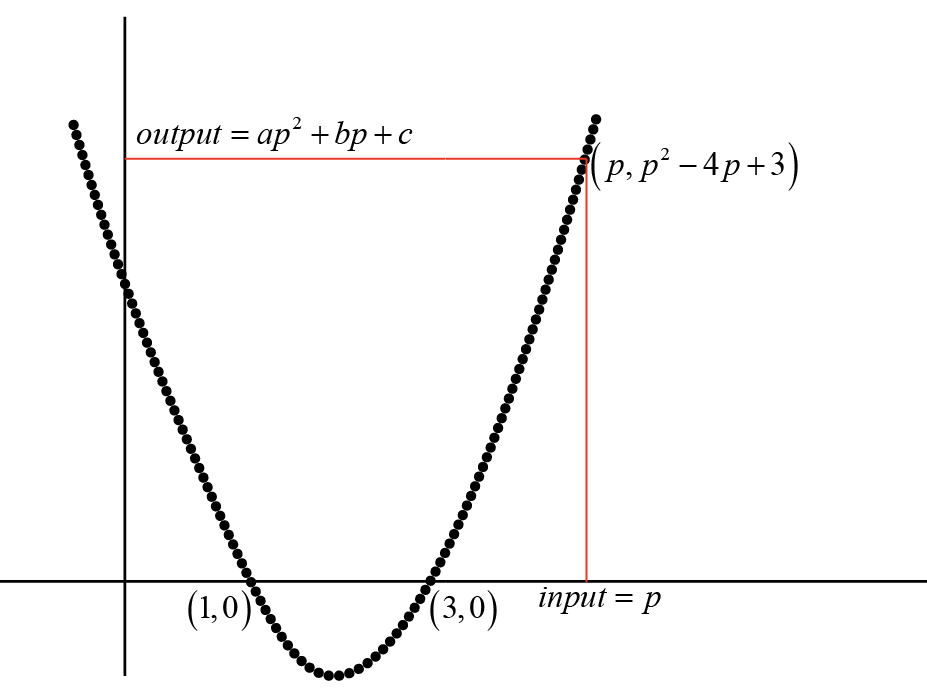
For the quadratic expression \( x^2 - 4x + 3 \), we can find the output for different inputs. For example:
- If we input \( x = 0 \), the output is 3, because \( 0^2 - 4 \times 0 + 3 = 3 \).
- With \( x = 1 \), the output is 0, making \( x = 1 \) a special input known as a root of the equation.
- An input of \( x = 2 \) gives us an output of \( -1 \), calculated by \( 2^2 - 4 \times 2 + 3 = -1 \).
Since \( x \) can be any number, there are infinitely many possible inputs. We can visualize these infinite input-output relationship using aa cartesian coordinate sytem. Each input and its output can be written as a pair of numbers, (input, output). For example, \( (0, 3) \), \( (1, 0) \), and \( (2, -1) \) are all pairs that we can place on a graph. Upon plotting all these infinite pairs on a graph, they don't just fall anywhere; they align to trace a specific curve. This alignment isn't random but rather a reflection of the inherent relationship dictated by the quadratic formula.
The curve that we visualize as a result of plotting a quadratic expression is the parabola. Its distinctive 'U' shape, whether it opens upwards like a cup or downwards like an umbrella, depends on the sign of the coefficient \( a \). The parabola is symmetrical and has a vertex, which is either the highest or lowest point of the curve.
While we're not going into the detailed method of plotting the entire graph, it's important to recognize how the graph's appearance varies with the values of \( a \) and the discriminant (commonly represented as \( \Delta \), and calculated as \( b^2 - 4ac \)). These determine the direction in which the parabola opens and whether it crosses the horizontal axis.
Different Possibilities of Graphs of a Quadratic Expression
Solving quadratic inequalities is a pivotal skill in algebra. To master this, one must become familiar with the foundational aspects of the graphs of quadratic expressions, especially how they vary based on two key parameters: the coefficient \( a \), and the discriminant \( \Delta \), where \( \Delta = b^2 - 4ac \).
The value of \( a \), the coefficient of the quadratic term \( x^2 \), dictates the direction in which the parabola—the graph of a quadratic expression—opens. If \( a \) is positive, the parabola opens upwards like a smile; if \( a \) is negative, it opens downwards like a frown. This aspect of the quadratic graph tells us about the general behavior of the expression's values—whether they tend to be positive or negative as \( x \) moves away from the vertex.
The discriminant \( \Delta \), on the other hand, gives us insight into the nature and position of the roots of the quadratic expression. It tells us whether the expression has two distinct real roots, one real repeated root, or no real roots at all. These roots are the points where the graph intersects the x-axis, and knowing their nature is crucial because it informs us about the intervals where the quadratic expression takes positive or negative values.
When we set out to solve a quadratic inequality, such as \( ax^2 + bx + c > 0 \) or \( ax^2 + bx + c < 0 \), our goal is to find the range of \( x \) values that make the inequality true. By visualizing the graph of the related quadratic expression \( ax^2 + bx + c \), we can intuitively determine these ranges. The graph acts as a guide, illustrating when the expression's values lie above or below the x-axis—corresponding to positive or negative values, respectively.
Consider a Quadratic Expression \( ax^2 + bx + c \). There six distinctive possibilities that you should know.
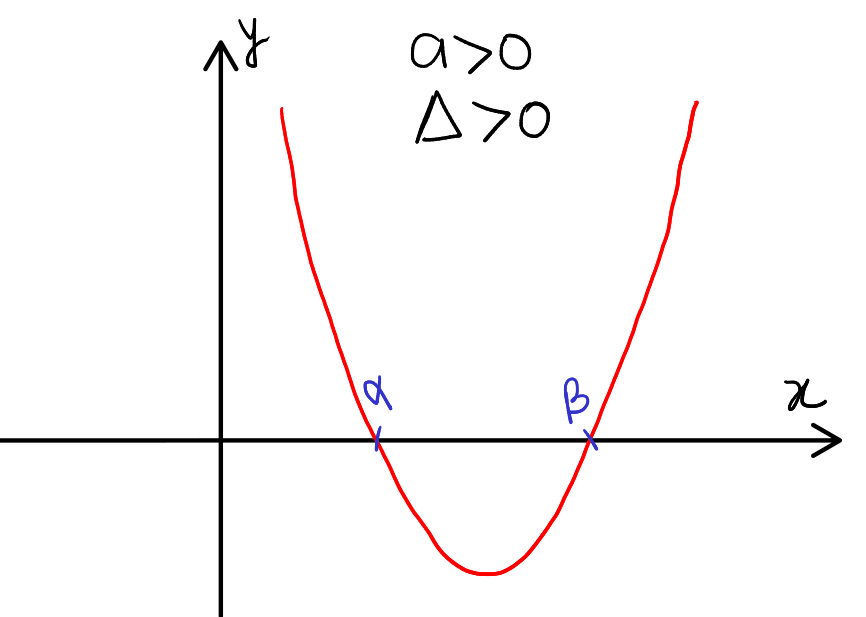
Case 1: Leading coefficient is positive and Discriminant is also positive
In this case, \(a>0\) indicates that the parabola opens upwards, and the discriminant being greater than zero indicates that there are two distinct real roots, labeled here as \( \alpha \) and \( \beta \).
For the inequality \( ax^2 + bx + c > 0 \), the solution set includes all values of \( x \) for which the quadratic expression is positive. Given the upward-opening parabola with roots \( \alpha \) and \( \beta \), the expression is positive outside the interval between the roots. This yields the solution as \( x \in (-\infty, \alpha) \cup (\beta, \infty) \).
Conversely, for the inequality \( ax^2 + bx + c < 0 \), the solution set is the interval between the roots where the parabola dips below the x-axis. Therefore, the solution is \( x \in (\alpha, \beta) \).
Example
Let's consider the inequality \( x^2 - 5x + 6 > 0 \) and \( x^2 - 5x + 6 < 0 \) with the quadratic expression \( x^2 - 5x + 6 \).
Firstly, factor the quadratic expression:
This expression has two distinct roots: \( x = 2 \) and \( x = 3 \). The parabola opens upwards since the coefficient of \( x^2 \) is positive.
Solve \( x^2 - 5x + 6 > 0 \):
For the expression to be greater than zero, we look for values of \( x \) outside the interval between the roots: The solution set is \( x \in (-\infty, 2) \cup (3, \infty) \).
Solve \( x^2 - 5x + 6 < 0 \):
For the expression to be less than zero, we seek values of \( x \) within the interval of the roots: The solution set is \( x \in (2, 3) \).
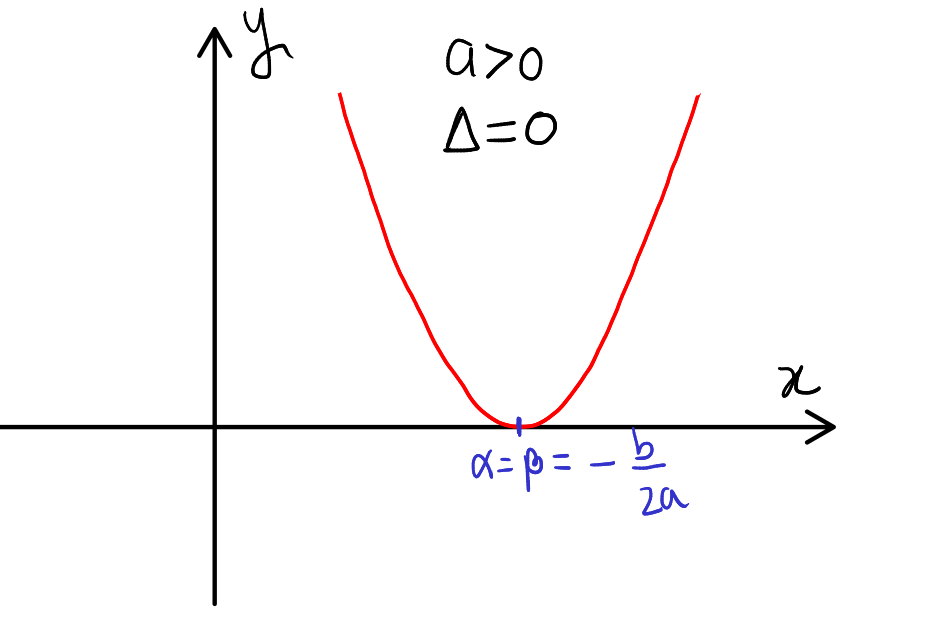
Case 2: Leading coefficient is positive and Discriminant is zero
When \( a > 0 \) and \( \Delta = 0 \), the quadratic expression \( ax^2 + bx + c \) represents a parabola that opens upwards and has its vertex lying on the x-axis. This vertex is the single solution to the equation \( ax^2 + bx + c = 0 \), and it occurs at \( x = -\frac{b}{2a} \). The significance of this single intersection point is that the quadratic expression will always yield non-negative values for all real numbers \( x \). Thus, the expression is never negative.
This understanding is neatly captured in a theorem which states:
Theorem:
If for a quadratic expression \( ax^2 + bx + c \), the coefficient \( a \) is positive and the discriminant \( \Delta \) is zero, then \( ax^2 + bx + c \geq 0 \) for all real numbers \( x \).
Example
Consider the quadratic expression \( x^2 + 18x + 81 \). To understand its behavior, let's first confirm that it's a perfect square by factoring it:
This factorization reveals that the expression is indeed a perfect square since it can be written as \( (x + 9) \) multiplied by itself. Therefore, our coefficient \( a \) is 1 (which is positive), and the discriminant \( \Delta \) is \( (18)^2 - 4(1)(81) = 0 \).
Given these conditions, we apply our theorem and conclude that \( x^2 + 18x + 81 \geq 0 \) for any real number \( x \). Graphically, this corresponds to a parabola that opens upwards and touches the x-axis at \( x = -9 \), its lone root and vertex.
Solving the inequalities \( x^2 + 18x + 81 > 0 \) and \( x^2 + 18x + 81 < 0 \) becomes straightforward with this visualization:
- For \( x^2 + 18x + 81 > 0 \), the solution set is all real numbers except \( x = -9 \).
- For \( x^2 + 18x + 81 < 0 \), there are no real solutions because the expression never yields a negative value for any real number \( x \).
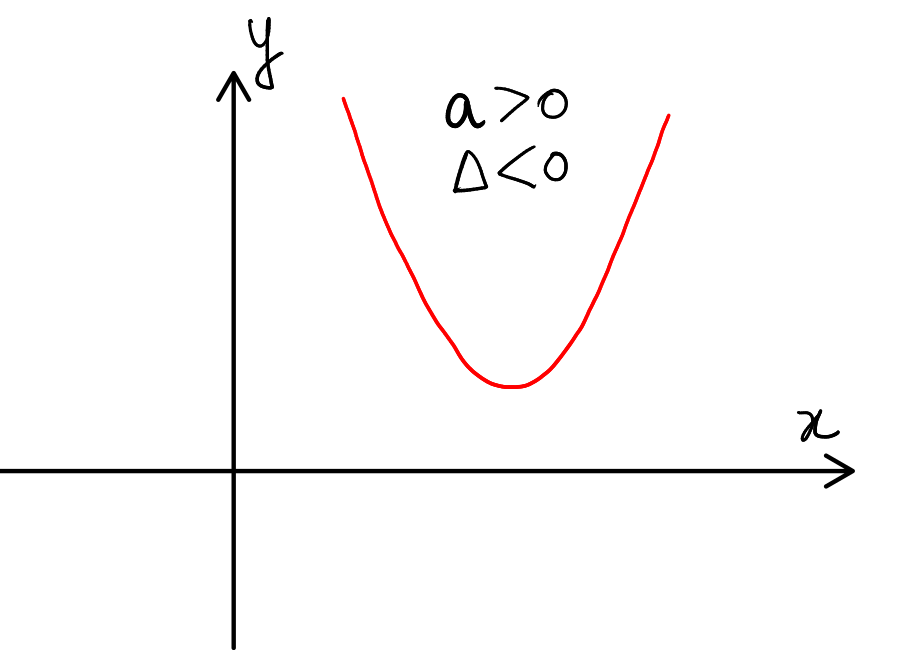
Case 3: Leading coefficient is positive and Discriminant is also negative
When we examine the graph of a quadratic expression with a positive leading coefficient \( a \) and a negative discriminant \( \Delta \), it shows a parabola that opens upward and does not intersect the x-axis at any point. If it never intersects the x-axis, it means there no real roots. This absence of real roots (x-intercepts) is a direct consequence of the negative discriminant (\( \Delta < 0 \)).
Implications of \( a > 0 \) and \( \Delta < 0 \):
For such a parabola, since it opens upwards and the vertex lies above the x-axis, the quadratic expression will always yield values greater than or equal to zero for all real numbers \( x \). The vertex represents the minimum value of the quadratic expression. No matter how far left or right along the x-axis we travel, the value of the quadratic expression remains non-negative.
Theorem:
If for a quadratic expression \( ax^2 + bx + c \), the coefficient \( a \) is positive (\( a > 0 \)) and the discriminant \( \Delta \) is negative (\( \Delta < 0 \)), then the expression \( ax^2 + bx + c \) is greater than or equal to zero (\( \geq 0 \)) for every real number \( x \). Moreover, the converse of this theorem is also true. If a quadratic expression is non-negative for all real numbers \( x \), then it must have \( a > 0 \) and \( \Delta \leq 0 \).
Example
Solve the inequation \( x^2 + x + 1 > 0 \).
To solve the inequality \( x^2 + x + 1 > 0 \), we consider the sign of \( a \), which is positive, and we calculate the discriminant:
Since the discriminant is negative, there are no real roots, and the parabola does not cross the x-axis. As a result, the expression \( x^2 + x + 1 \) will always be positive for all real numbers \( x \). The solution to the inequality is therefore all real numbers, \( x \in \mathbb{R} \).
Example
Solve the inequality:
Solution:
We first examine the quadratic expression \( x^2 - 2x + 6 \).
Step 1: Determine the nature of the quadratic expression \( x^2 - 2x + 6 \):
The coefficient \( a \) is positive, and we calculate the discriminant \( \Delta \):
Since \( \Delta < 0 \), there are no real roots for the quadratic expression, and thus, it is always positive for any real number \( x \). Given that this part of the expression is always positive, it will not affect the sign of the inequality.
Step 2: Simplify the inequality:
We can ignore \( x^2 - 2x + 6 \) as it is always positive and simplify the inequality to:
Step 3: Solve the simplified inequality:
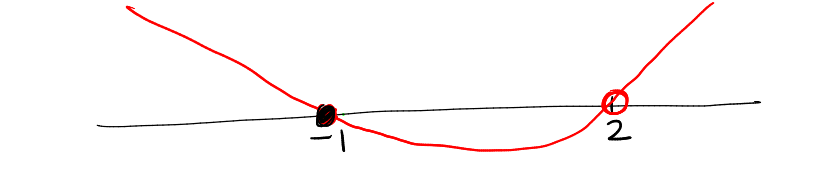
To solve \( \frac{x + 1}{x - 2} \geq 0 \), we draw a wavy curve that considers the zeros of the numerator \( x + 1 \) and the undefined point of the denominator \( x - 2 \):
- The numerator \( x + 1 \) is zero at \( x = -1 \).
- The denominator \( x - 2 \) is zero (and the expression is undefined) at \( x = 2 \).
We plot these points on the number line and determine the intervals where the expression is positive or negative by drawing a wavy curve through these points:
The wavy curve crosses the x-axis at \( x = -1 \) and has an undefined point at \( x = 2 \).
Step 4: Write the solution set:
Based on the wavy curve, the solution to \( \frac{x + 1}{x - 2} \geq 0 \) includes the intervals where the expression is positive or zero. The solution set is:
This includes \( x = -1 \) since at this point the expression is equal to zero, which satisfies the inequality. The point \( x = 2 \) is not included because the expression is undefined there.
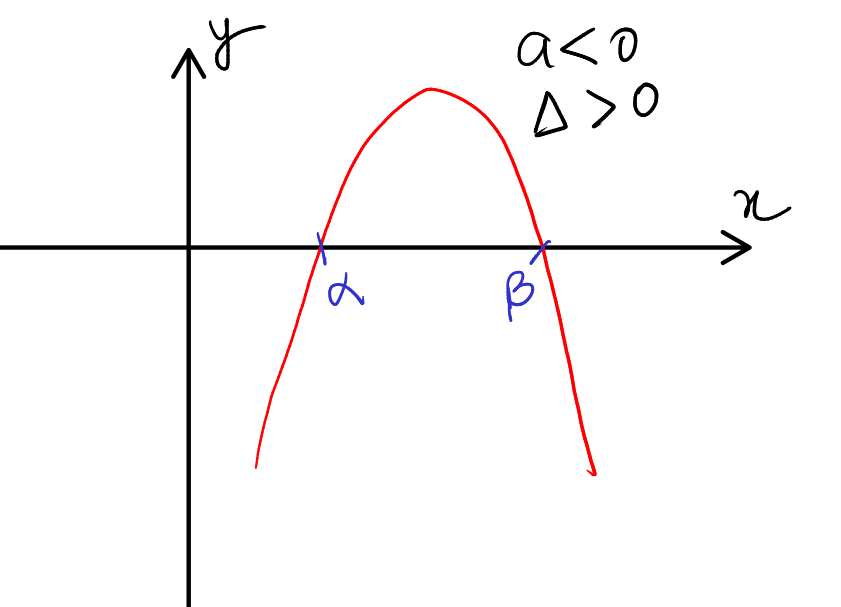
Case 4: Leading Coefficient Negative and Discriminant Positive
In this case, where the leading coefficient \( a \) of the quadratic expression \( ax^2 + bx + c \) is negative (\( a < 0 \)), and the discriminant (\( \Delta \)) is positive (\( \Delta > 0 \)), the graph is characterized by a downward-opening parabola that intersects the x-axis at two distinct points. The positive discriminant indicates the parabola will intersect the x-axis at two distinct points, which are the real and distinct solutions (roots) of the equation \( ax^2 + bx + c = 0 \).
Inequality Solutions for \( ax^2 + bx + c > 0 \):
Given the downward orientation of the parabola, the expression \( ax^2 + bx + c \) will be greater than zero in the intervals where the graph is above the x-axis, which occurs between the roots. Therefore, the solution for the inequality \( ax^2 + bx + c > 0 \) is:
Inequality Solutions for \( ax^2 + bx + c < 0 \):
Conversely, the expression will be less than zero where the graph lies below the x-axis, which is to the left of the smaller root and to the right of the larger root. Hence, the solution for the inequality \( ax^2 + bx + c < 0 \) is:
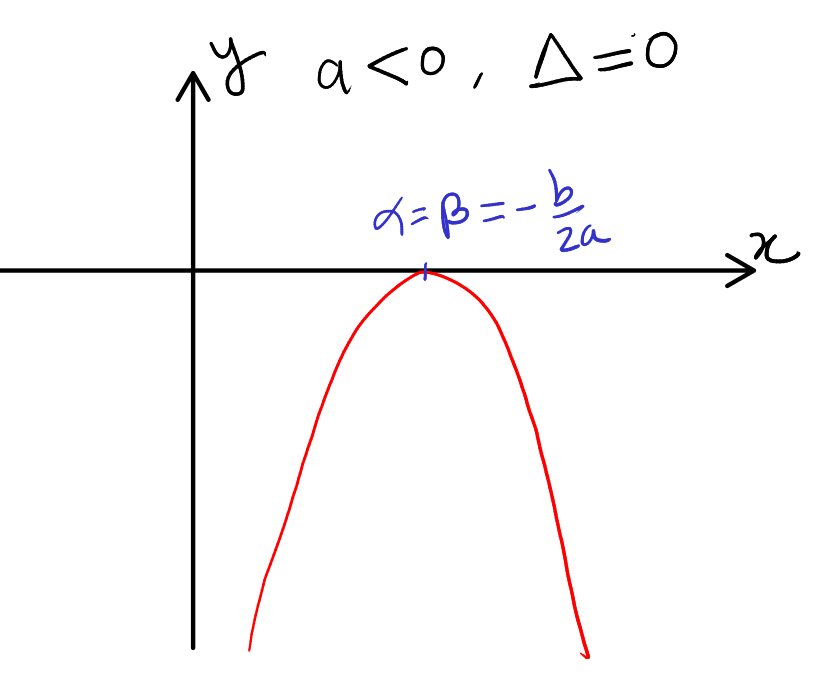
Case 5: Leading Coefficient Negative and Discriminant Zero
In this case, the quadratic expression \( ax^2 + bx + c \) has a negative leading coefficient (\( a < 0 \)) and a discriminant (\( \Delta \)) of zero (\( \Delta = 0 \)). This particular combination leads to a graph that displays a downward-opening parabola which touches the x-axis at exactly one point, often referred to as the vertex of the parabola.
If the leading coefficient \( a \) is negative and the discriminant \( \Delta \) is zero, the quadratic expression \( ax^2 + bx + c \) is always less than or equal to zero for all real numbers \( x \). This is symbolically represented as:
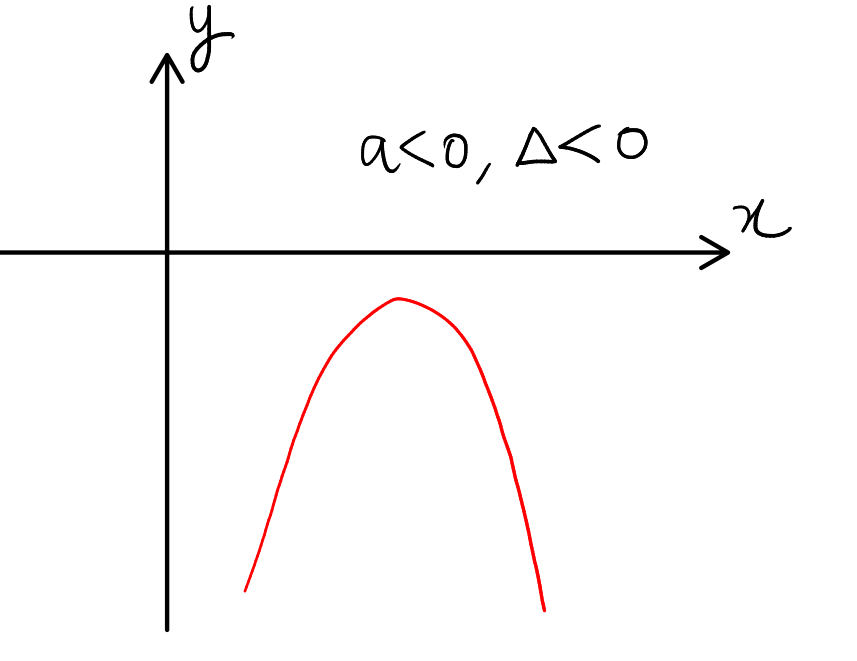
Case 6: Leading Coefficient Negative and Discriminant Negative
For a quadratic expression \( ax^2 + bx + c \) where the leading coefficient \( a \) is negative (\( a < 0 \)) and the discriminant (\( \Delta \)) is negative (\( \Delta < 0 \)), the graph is a parabola that opens downwards and has no real intersections with the x-axis, which means that the entire graph of the quadratic expression lies below the x-axis.
If the leading coefficient \( a \) is negative and the discriminant \( \Delta \) is negative for the quadratic expression \( ax^2 + bx + c \), then the expression is strictly less than zero for all real numbers \( x \). This can be formally stated as:
Conclusion
The six cases of quadratic expressions categorized by the signs of the leading coefficient \( a \) and the discriminant \( \Delta \) provide a comprehensive framework for solving quadratic inequalities. This framework is grounded in understanding the shape and position of the parabola on the graph, which is determined by these two parameters.
- When \( a > 0 \) and \( \Delta > 0 \), the parabola opens upwards with two distinct real roots, and the expression is positive outside the interval between the roots.
- If \( a > 0 \) and \( \Delta = 0 \), the parabola opens upwards, touching the x-axis at one point, the vertex, and the expression is non-negative for all real numbers.
- When \( a > 0 \) and \( \Delta < 0 \), the parabola again opens upwards but has no real roots, remaining positive for all real numbers.
- For \( a < 0 \) and \( \Delta > 0 \), the parabola opens downwards with two real roots, and the expression is negative outside the interval between the roots.
- If \( a < 0 \) and \( \Delta = 0 \), the downward-opening parabola touches the x-axis at the vertex, and the expression is non-positive for all real numbers.
- Lastly, when \( a < 0 \) and \( \Delta < 0 \), the parabola opens downwards without intersecting the x-axis, making the expression strictly negative for all real numbers.
By identifying which of these six cases applies to a given quadratic inequality, we can immediately determine the intervals on the real number line where the expression is positive or negative. This significantly simplifies the process of finding the solution sets for inequalities such as \( ax^2 + bx + c > 0 \) or \( ax^2 + bx + c < 0 \), as we can infer the behavior of the quadratic expression without having to perform the complete square or use other algebraic methods.