Interaction of Points with a Line

Introduction

Given a point \( P(x_1, y_1) \) and a line described by the equation \( ax + by + c = 0 \), we explore three significant geometric concepts:

1. The perpendicular distance from point \( P \) to the line is the shortest distance between the point and any point on the line. It is measured along the line perpendicular to the given line passing through \( P \).

2. The foot of the perpendicular from \( P \) to the line is the point of intersection of the line and the perpendicular drawn from \( P \). This point is significant as it is the closest point on the line to \( P \).

3. The image of point \( P \) in the line is the point \( P' \) such that \( P \) and \( P' \) are symmetric with respect to the line. The line segment connecting \( P \) and \( P' \) is bisected by the line, and this segment is perpendicular to the line.

Perpendicular Distance of a Point from a Line

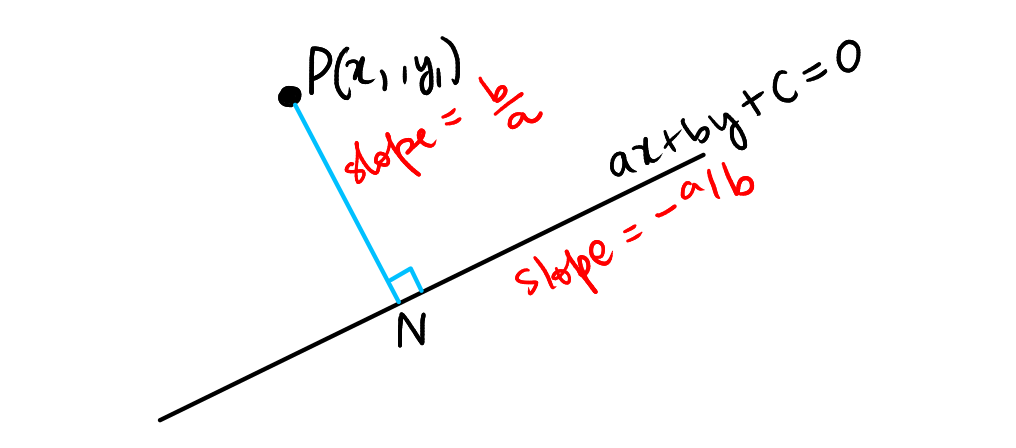
Let \( P(x_1, y_1) \) be a point in the plane and let \( ax + by + c = 0 \) be the equation of a non-vertical line. The perpendicular distance \( d \) from the point \( P \) to the line is given by the formula:

\[ d = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}} \]

Proof:

To find the perpendicular distance of a point \( P(x_1, y_1) \) from the line \( ax + by + c = 0 \), we construct a line perpendicular to \( ax + by + c = 0 \) that passes through point \( P \). This perpendicular intersects the given line at point \( N \), which is the foot of the perpendicular from \( P \).

The slope of the given line is \( -\frac{a}{b} \), thus the slope of the perpendicular line \( PN \) is \( \frac{b}{a} \). If the angle this line makes with the positive x-axis is \( \theta \), then \( \tan(\theta) = \frac{b}{a} \). Using trigonometric identities, we find:

\[ \cos(\theta) = \frac{a}{\sqrt{a^2 + b^2}} \quad \text{and} \quad \sin(\theta) = \frac{b}{\sqrt{a^2 + b^2}} \]

The symmetric form of the equation of line \( PN \) is given by:

\[ \frac{x - x_1}{\cos(\theta)} = \frac{y - y_1}{\sin(\theta)} = r \]

The coordinates of \( N \) can be represented as \( (x_1 + r\cos(\theta), y_1 + r\sin(\theta)) \) for some value of \( r \). Since \( N \) lies on the line \( ax + by + c = 0 \), we substitute the coordinates of \( N \) into the line equation and solve for \( r \), yielding:

\[ a(x_1 + r\cos(\theta)) + b(y_1 + r\sin(\theta)) + c = 0 \]

Substituting \( \cos(\theta) = \frac{a}{\sqrt{a^2 + b^2}} \) and \( \sin(\theta) = \frac{b}{\sqrt{a^2 + b^2}} \) yields:

\[ a\left(x_1 + r\frac{a}{\sqrt{a^2 + b^2}}\right) + b\left(y_1 + r\frac{b}{\sqrt{a^2 + b^2}}\right) + c = 0 \]

Solving for \( r \):

\[ ar\frac{a}{\sqrt{a^2 + b^2}} + br\frac{b}{\sqrt{a^2 + b^2}} = -ax_1 - by_1 - c \]

\[ r\left(\frac{a^2}{\sqrt{a^2 + b^2}} + \frac{b^2}{\sqrt{a^2 + b^2}}\right) = -ax_1 - by_1 - c \]

Recognizing that \( \frac{a^2}{\sqrt{a^2 + b^2}} + \frac{b^2}{\sqrt{a^2 + b^2}} = \sqrt{a^2 + b^2} \):

\[ r\sqrt{a^2 + b^2} = -ax_1 - by_1 - c \]

Simplifying and solving for \( r \) we obtain:

\[ r = -\frac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}} \]

The absolute value \( |r| \) gives the actual perpendicular distance.

Coordinates of foot of perpendicular dropped from a point to a line

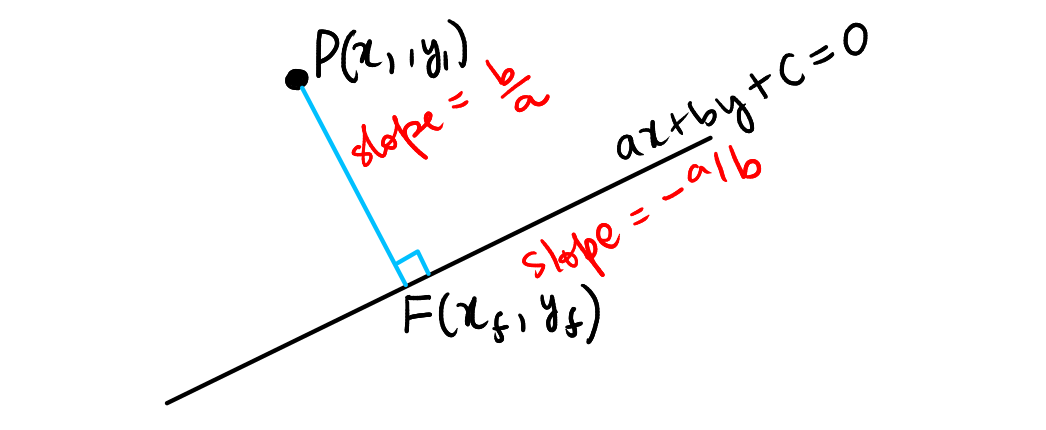
The coordinates \( (x_f, y_f) \) of the foot of a perpendicular dropped from a point \( (x_1, y_1) \) to the line \( ax + by + c = 0 \) are given by the following relations:

\[ \frac{x_f - x_1}{a} = \frac{y_f - y_1}{b} = -\frac{ax_1 + by_1 + c}{a^2 + b^2} \]

Proof:

Draw a perpendicular from \( P(x_1, y_1) \) to the line \( ax + by + c = 0 \) having foot at \( F(x_f, y_f) \).

Slope of the given line is \( -\frac{a}{b} \). Then the slope of \( PF \) is \( \frac{b}{a} \). If \( PF \) makes an angle \( \theta \) with the positive x-axis, then \( \tan\theta = \frac{b}{a} \). This implies that \( \sin\theta = \frac{b}{\sqrt{a^2 + b^2}} \) and \( \cos\theta = \frac{a}{\sqrt{a^2 + b^2}} \).

We write the symmetric form of \( PF \) as \( \frac{x - x_1}{\cos\theta} = \frac{y - y_1}{\sin\theta} = r \).

Thus coordinates of \( F \) are \( x_f = x_1 + r_f \cos\theta \) and \( y_f = y_1 + r_f \sin\theta \) for some \( r = r_f \).

F also lies on \( ax + by + c = 0 \)

\( \Rightarrow ax_f + by_f + c = 0 \)

\( \Rightarrow a(x_1 + r_f \cos\theta) + b(y_1 + r_f \sin\theta) + c = 0 \)

\( \Rightarrow r_f = - \frac{ax_1 + by_1 + c}{a \cos\theta + b \sin\theta} \)

But \( a \cos\theta + b \sin\theta = \frac{a^2}{\sqrt{a^2 + b^2}} + \frac{b^2}{\sqrt{a^2 + b^2}} \)

\( = \sqrt{a^2 + b^2} \)

Thus, \( \frac{x_f - x_1}{\cos\theta} = \frac{y_f - y_1}{\sin\theta} = - \frac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}} \)

\( \Rightarrow \frac{x_f - x_1}{a/\sqrt{a^2+b^2}} = \frac{y_f - y_1}{b/\sqrt{a^2+b^2}} = - \frac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}} \)

\( \Rightarrow \frac{x_f - x_1}{a} = \frac{y_f - y_1}{b} = - \frac{ax_1 + by_1 + c}{a^2 + b^2} \)

\(\blacksquare\)

Image of a point with respect to a line

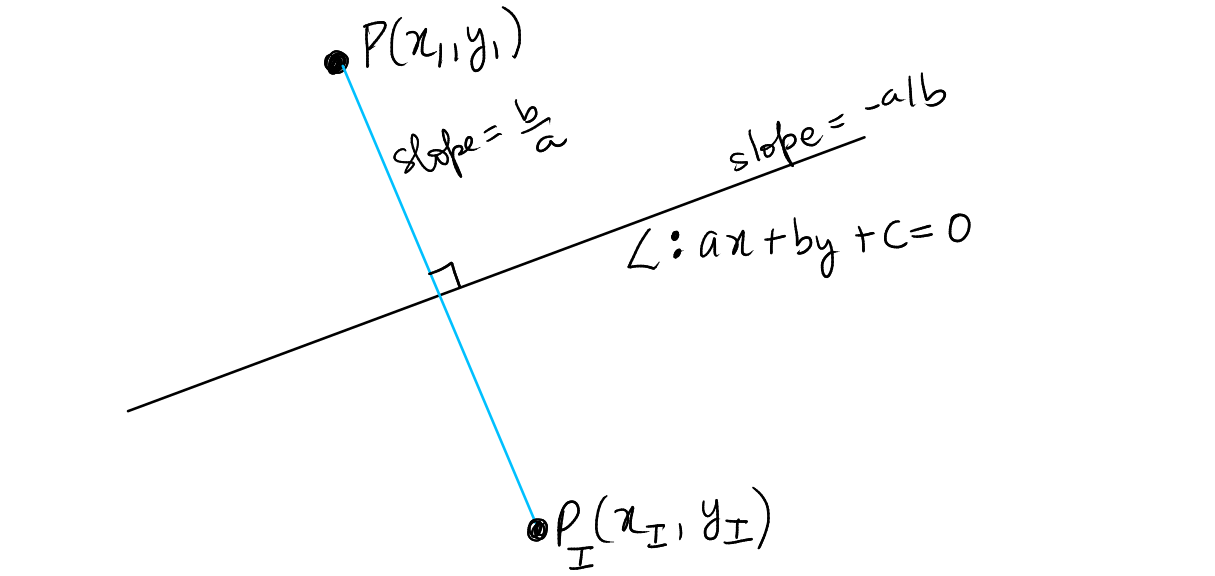
The image \((x_I, y_I)\) of the point \((x_1, y_1)\) in the line \(ax+by+c=0\) is given by the relation:

\[ \frac{x_I - x_1}{a} = \frac{y_I - y_1}{b} = -\frac{2(ax_1 + by_1 + c)}{a^2 + b^2} \]

Proof:

The image \(P_I(x_I, y_I)\) of the point \(P(x_1, y_1)\) in the line \(L: ax+by+c=0\) can be found using the following procedure:

Draw the line joining \(P\) and \(P_I\) cutting \(L\) at \(F\). Clearly \(F\) is the midpoint of \(P\) and \(P_I\) and \(PP_I\) is perpendicular to \(L\).

Slope of \(L\) is \(-\frac{a}{b}\) => Slope of \(PP_I\) is \(\frac{b}{a}\).

Let \(PP_I\) make an angle \(\theta\) with positive x-axis. Then, \(\tan\theta = \frac{b}{a}\) => \(\cos\theta = \frac{a}{\sqrt{a^2+b^2}}\) and \(\sin\theta = \frac{b}{\sqrt{a^2+b^2}}\).

The symmetric form of the line \(PP_I\) is \(\frac{x-x_1}{\cos\theta} = \frac{y-y_1}{\sin\theta} = r\).

Then, coordinates of \(P_I\) can be written as: \(x_I = x_1 + r_I \cos\theta\) and \(y_I = y_1 + r_I \sin\theta\) for some \(r=r_I\).

Midpoint of \(P\) and \(P_I\) is \(F\) which lies on \(L\). Therefore,

\(a\left(\frac{x_1 + x_I}{2}\right) + b\left(\frac{y_1 + y_I}{2}\right) + c = 0\)

\(\Rightarrow a\left(2x_1 + r_I\cos\theta\right) + b\left(2y_1 + r_I\sin\theta\right) + 2c = 0\)

\(\Rightarrow r_I = -2\left(\frac{ax_1 + by_1 + c}{a\cos\theta + b\sin\theta}\right)\)

Now \(a\cos\theta + b\sin\theta = \frac{a^2}{\sqrt{a^2+b^2}} + \frac{b^2}{\sqrt{a^2+b^2}} = \sqrt{a^2+b^2}\)

\(\therefore r_I = -2\left(\frac{ax_1 + by_1 + c}{\sqrt{a^2+b^2}}\right)\)

\(\therefore \frac{x_I - x_1}{a/\sqrt{a^2+b^2}} = \frac{y_I - y_1}{b/\sqrt{a^2+b^2}} = -2\left(\frac{ax_1 + by_1 + c}{a^2+b^2}\right)\)

\(\Rightarrow \frac{x_I - x_1}{a} = \frac{y_I - y_1}{b} = \frac{-2\left(ax_1 + by_1 + c\right)}{a^2+b^2}\) \(\blacksquare\)

Distance of a point from a line measured along another line

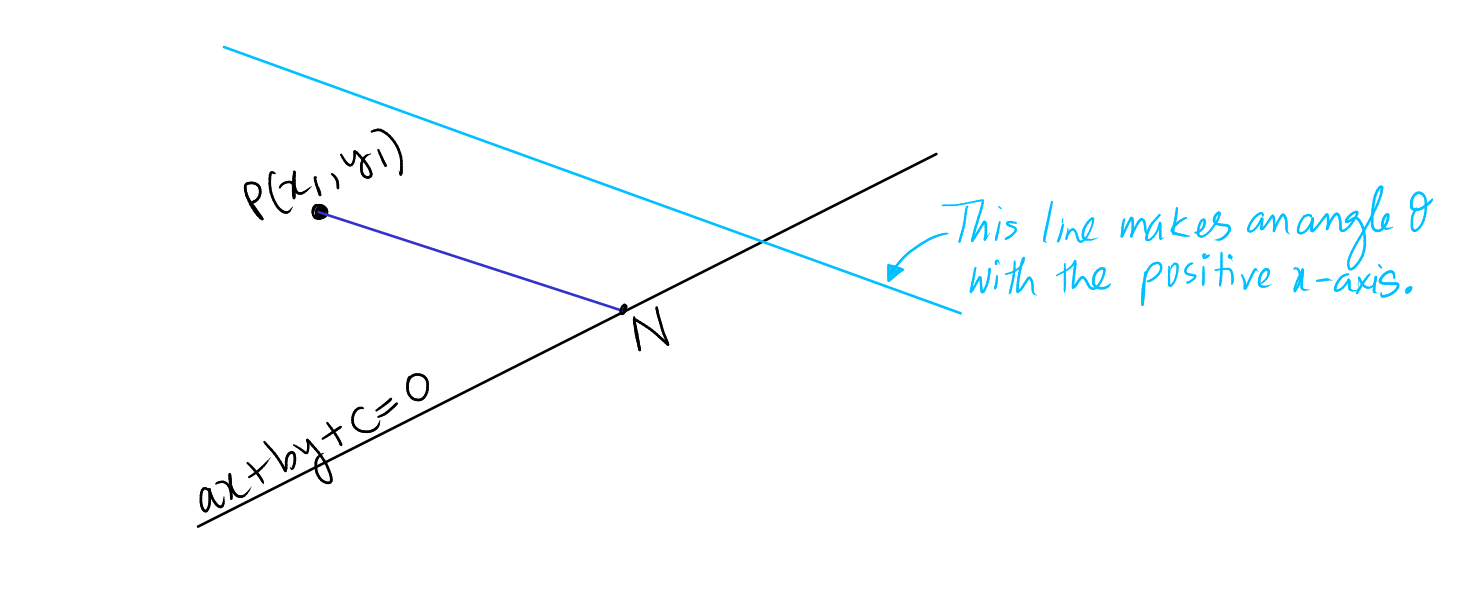
The distance \( d \) of a point \( P(x_1, y_1) \) from the line \( ax + by + c = 0 \) measured along another line which makes an angle \( \theta \) with the positive x-axis is given by:

\[ d = \frac{|ax_1 + by_1 + c|}{|a\cos\theta + b\sin\theta|} \]

Proof:

To prove the distance of a point \( P(x_1, y_1) \) from a line \( ax + by + c = 0 \) measured along another line making an angle \( \theta \) with the positive x-axis:

Draw a line \( PN \) parallel to the line which makes an angle of \( \theta \) with the positive x-axis. The equation of \( PN \) in symmetric form is \( \frac{x - x_1}{\cos\theta} = \frac{y - y_1}{\sin\theta} = r \). Thus, the coordinates of \( N \) can be written as \( x = x_1 + r\cos\theta \) and \( y = y_1 + r\sin\theta \) for some \( r \) in \( \mathbb{R} \).

Since \( N \) lies on the line \( ax + by + c = 0 \), substituting the coordinates of \( N \) we get \( a(x_1 + r\cos\theta) + b(y_1 + r\sin\theta) + c = 0 \). Solving for \( r \) gives \( r = -\frac{ax_1 + by_1 + c}{a\cos\theta + b\sin\theta} \).

Thus, \( PN = |r| = \left| -\frac{ax_1 + by_1 + c}{a\cos\theta + b\sin\theta} \right| \).

This results in the formula for the distance of a point from a line along a given direction:

\[ d = \left| \frac{ax_1 + by_1 + c}{a\cos\theta + b\sin\theta} \right| \]

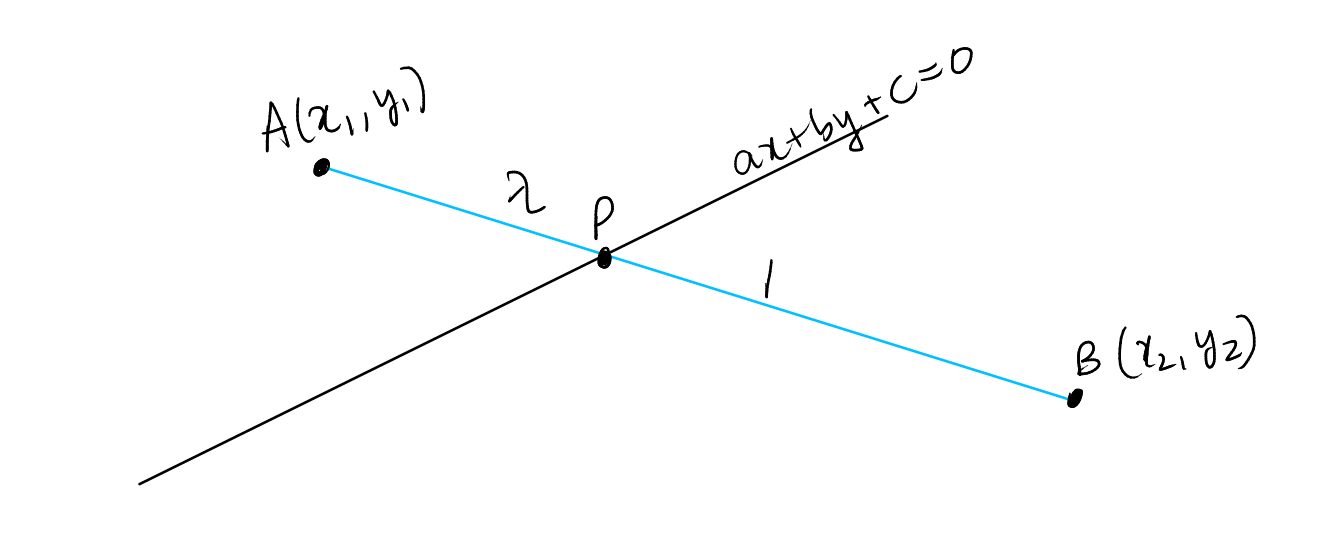
Ratio in which a line divides the line segment joining two points

The ratio in which the line \( ax + by + c = 0 \) divides the line segment joining points \( A(x_1, y_1) \) and \( B(x_2, y_2) \) is given by:

\[ \text{Ratio}= \lambda = -\frac{ax_1 + by_1 + c}{ax_2 + by_2 + c} \]

Proof:

Let the line \( ax + by + c = 0 \) divide the line joining \( A(x_1, y_1) \) and \( B(x_2, y_2) \) in the ratio \(\lambda : 1\). Let it cut \( AB \) at \( P \).

Thus, \( \frac{AP}{PB} = \lambda \).

Coordinates of \( P \) thus, are

\[ \left( \frac{\lambda x_2 + x_1}{\lambda + 1}, \frac{\lambda y_2 + y_1}{\lambda + 1} \right) \]

\( P \) lies on \( ax + by + c = 0 \)

Thus, substituting \( P \)'s coordinates:

\[ a\left( \frac{\lambda x_2 + x_1}{\lambda + 1} \right) + b\left( \frac{\lambda y_2 + y_1}{\lambda + 1} \right) + c = 0 \]

Multiply through by \( \lambda + 1 \) to clear the denominator:

\[ a(\lambda x_2 + x_1) + b(\lambda y_2 + y_1) + c(\lambda + 1) = 0 \]

Reorganize and isolate terms involving \( \lambda \):

\[ \lambda (ax_2 + by_2+c) + ax_1 + by_1 + c = 0 \]

Solve for \( \lambda \):

\[ \lambda (ax_2 + by_2+c) = -(ax_1 + by_1 + c) \]

\[ \lambda = -\frac{(ax_1 + by_1 + c)}{(ax_2 + by_2+c)} \]

\(\blacksquare\)

Example

Determine the ratio in which the line \(x + 2y + 1 = 0\) divides the line segment joining points \(A(2, 1)\) and \(B(-1, 3)\).

Solution:

To find the ratio, use the formula derived:

\[ \text{Ratio} = -\frac{ax_1 + by_1 + c}{ax_2 + by_2 + c} \]

Here, \(a = 1\), \(b = 2\), and \(c = 1\). The coordinates for \(A\) are \(x_1 = 2\), \(y_1 = 1\) and for \(B\) are \(x_2 = -1\), \(y_2 = 3\).

Plugging in these values:

\[ \text{Ratio} = -\frac{(1 \times 2) + (2 \times 1) + 1}{(1 \times -1) + (2 \times 3) + 1} \]

\[ \text{Ratio} = -\frac{2 + 2 + 1}{-1 + 6 + 1} \]

\[ \text{Ratio} = -\frac{5}{6} \]

Thus, the line \(x + 2y + 1 = 0\) divides the line segment joining points \(A(2, 1)\) and \(B(-1, 3)\) in the ratio of \(-\frac{5}{6}\).

This result indicates that the division is external, and the line passes through a point closer to \(A\) than \(B\) on the line segment \(AB\).

Relative Position of two points with respect to a line

Given a line \( L(x, y): ax + by + c = 0 \) and two points \( A(x_1, y_1) \) and \( B(x_2, y_2) \):

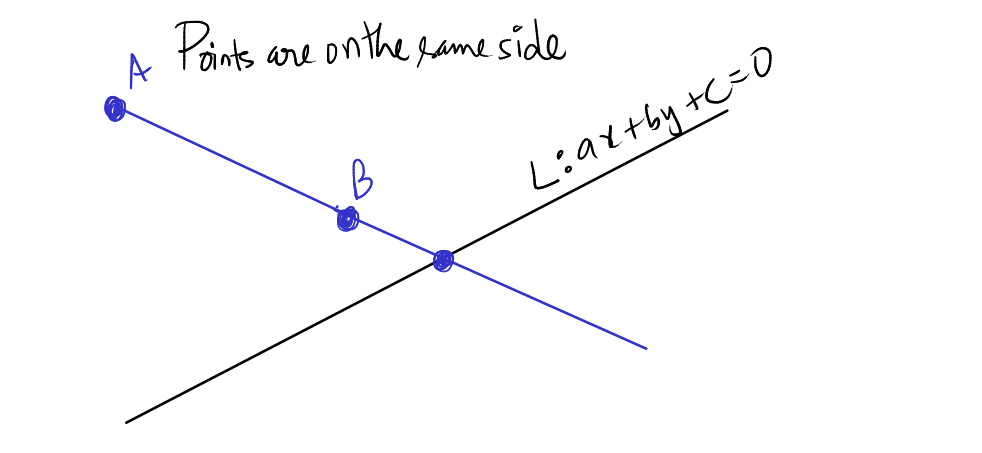
• The points \( A \) and \( B \) are on the same side of the line \( L \) if the expression \((ax_1 + by_1 + c)(ax_2 + by_2 + c) > 0\). As a short notation, we can write as \( L(x_1, y_1) \times L(x_2, y_2) > 0 \).

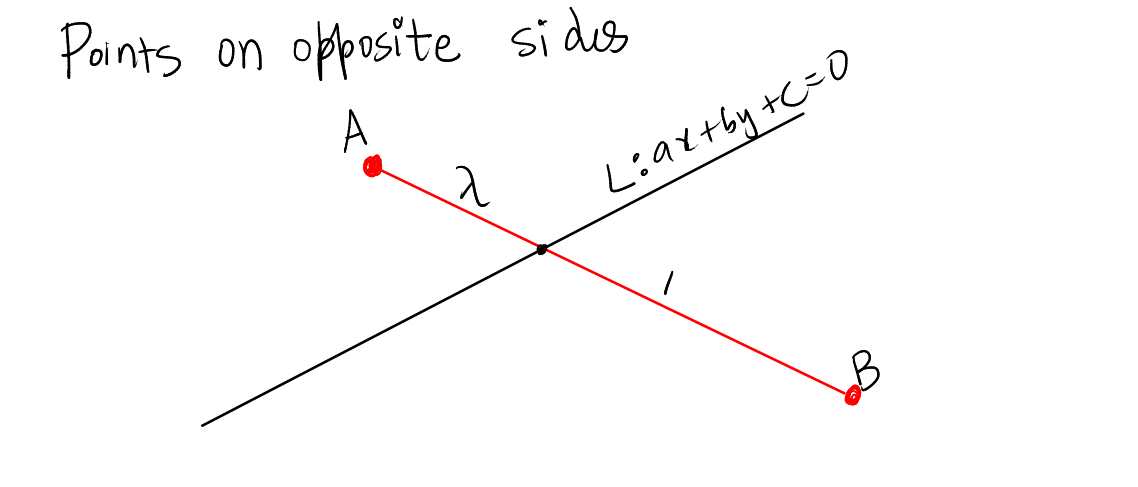
• The points \( A \) and \( B \) are on opposite sides of the line \( L \) if the expression \((ax_1 + by_1 + c)(ax_2 + by_2 + c) < 0\). As a short notation, we can write as \( L(x_1, y_1) \times L(x_2, y_2) < 0 \).

This theorem is used to determine the relative position of two points with respect to a given line without proving their actual positions.

Proof:

To prove the relative positions of two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\) with respect to the line \(L: ax+by+c=0\), we utilize the concept that if two points are on the same side of the line, then the line \(L\) divides the line segment \(AB\) externally, and the ratio \(\lambda = -\frac{(ax_1 + by_1 + c)}{(ax_2 + by_2 + c)}\) is negative. This is to say that \(-\frac{(ax_1 + by_1 + c)}{(ax_2 + by_2 + c)} < 0\) implies \(\frac{(ax_1 + by_1 + c)}{(ax_2 + by_2 + c)} > 0\), which leads to \((ax_1 + by_1 + c)(ax_2 + by_2 + c) > 0\).

If they are on opposite sides, then the line \(L\) divides \(AB\) internally and thus the ratio \(\lambda = -\frac{(ax_1 + by_1 + c)}{(ax_2 + by_2 + c)} > 0\) implies \((ax_1 + by_1 + c)(ax_2 + by_2 + c) < 0\). This shows that the products of their algebraic distances from the line have opposite signs, confirming that the points lie on opposite sides of the line. \(\blacksquare\)

A line divides a plane into two halves

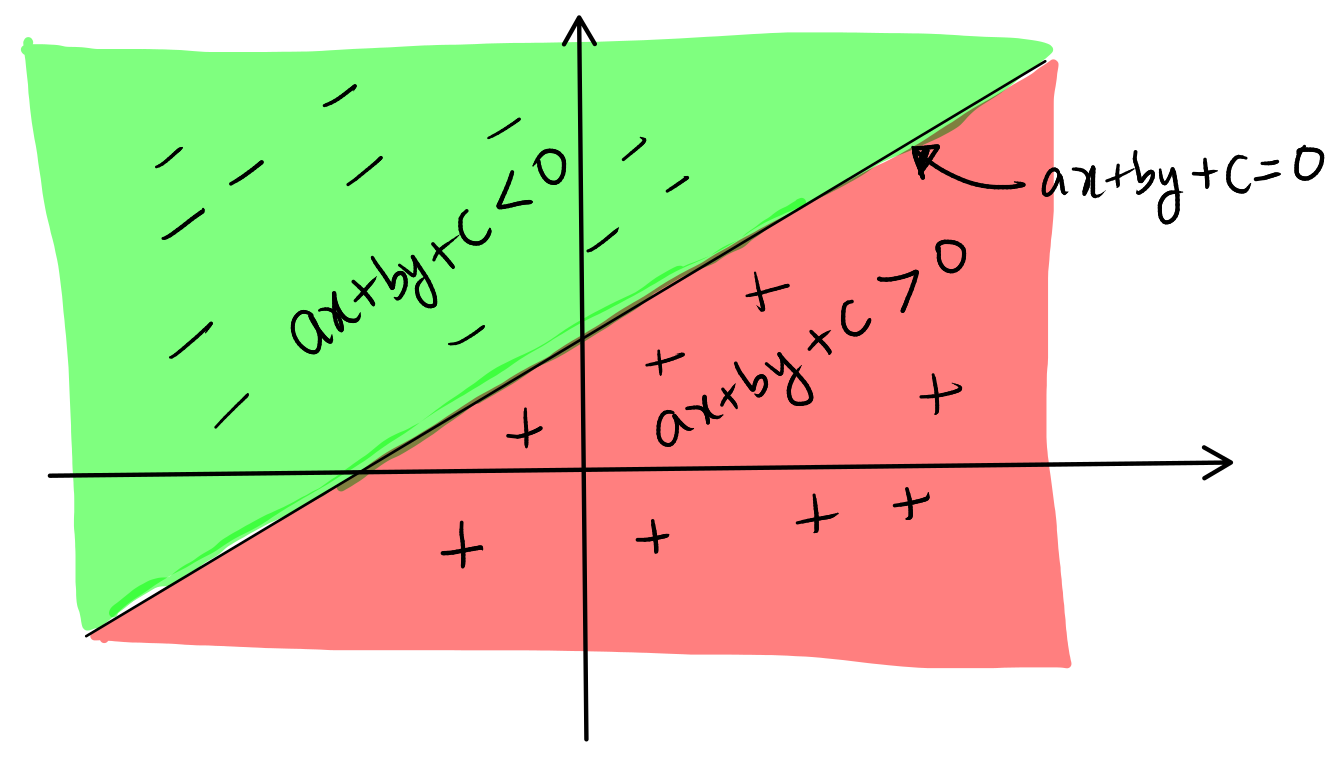
From above theorem we can conclude that the line \( ax + by + c = 0 \) divides the Euclidean plane into two distinct half-planes. To understand the classification of points in these regions, consider a point \((x, y)\) not on the line. There are two cases for the expression \( ax + by + c \):

1. Positive Region: If \( ax + by + c > 0 \), the point \((x, y)\) lies in the region where all points satisfy this inequality. This region is referred to as the positive half-plane relative to the line.

2. Negative Region: Conversely, if \( ax + by + c < 0 \), the point \((x, y)\) is in the region where all points satisfy this inequality, known as the negative half-plane.

The line \( ax + by + c = 0 \) itself is the boundary between these two regions. It serves as the set of points that neither belong to the positive nor the negative region but exactly satisfy the linear equation. Each point on this line is equidistant from both regions, underlining the line's role as a divider of the plane based on the sign of the linear expression \( ax + by + c \).

To determine which half-plane corresponds to \( ax + by + c > 0 \) and which corresponds to \( ax + by + c < 0 \), it is practical to use a test point. This point should be easy to evaluate and not lie on the line \( ax + by + c = 0 \).

A common choice for a test point is the origin (0,0) if it is not on the line. Substituting \( x = 0 \) and \( y = 0 \) into the equation, the sign of \( c \) provides immediate insight:

• If \( c > 0 \), then at the origin, \( ax + by + c = c > 0 \). Therefore, the half-plane containing the origin is the positive region.
• If \( c < 0 \), then \( ax + by + c = c < 0 \). This implies the half-plane containing the origin is the negative region.

If the origin lies on the line, or if another specific region needs to be checked, choose another simple point like \( (\alpha,0) \) or \( (0,\beta) \), assuming that we are sure that they do not lie on the line. Evaluating the line equation at this point will indicate the nature of the region similarly.

By testing such points, one can effectively categorize the two regions created by the line without complex calculations. This method of using test points simplifies the classification of regions in linear inequalities.

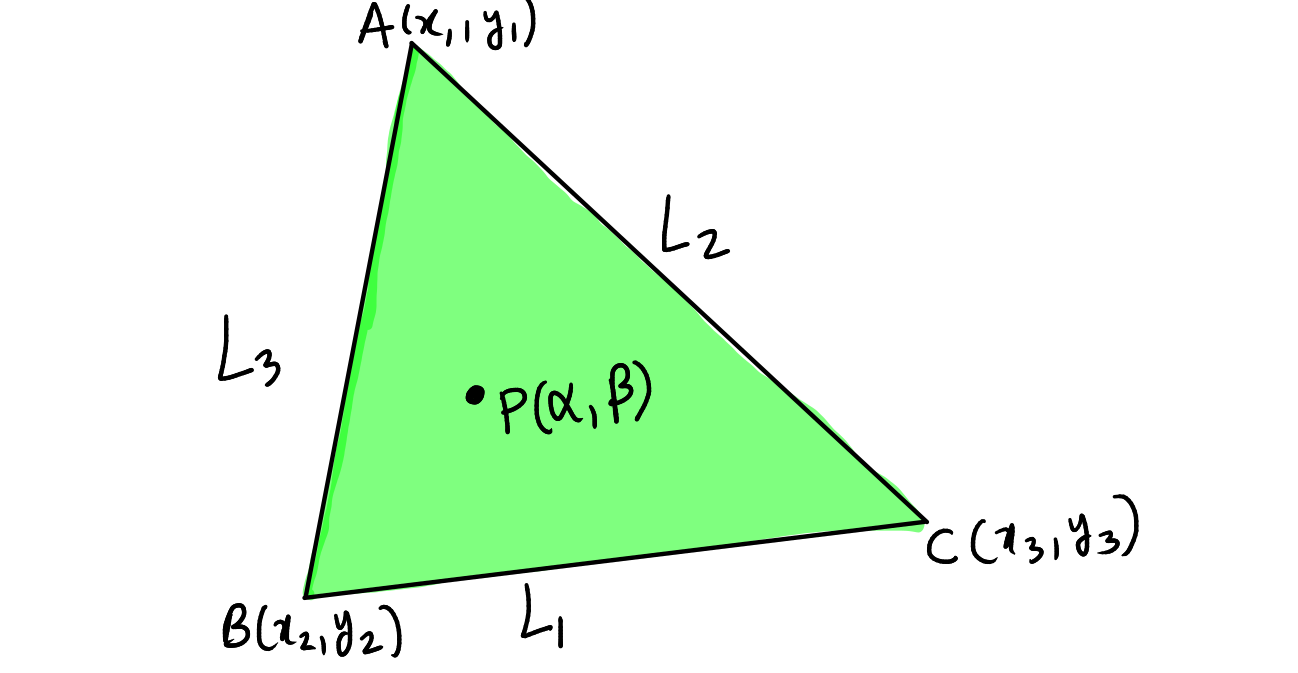
A point lies inside a triangle

Using Relative location of points

Consider a triangle \( \triangle ABC \) where vertices \( A \) are given as \( (x_1, y_1) \), \( B \) as \( (x_2, y_2) \), and \( C \) as \( (x_3, y_3) \). We want to determine if \( P(\alpha, \beta) \) lies inside the triangle. We can do this plotting all points. But, it is not necessary to plot all points. Instead, this can be determined algebraically by finding the line equations for each of the triangle's sides, denoted as \( L_1 \), \( L_2 \), and \( L_3 \).

These equations represent the sides \( BC \), \( CA \), and \( AB \) respectively. To establish if \( P \) is within \( \triangle ABC \), it should lie on the same side of each line as the opposite vertex of the triangle. Specifically:

• \( P \) and \( A \) must be on the same side of \( L_1 \) (line \( BC \)).
• \( P \) and \( B \) must be on the same side of \( L_2 \) (line \( CA \)).
• \( P \) and \( C \) must be on the same side of \( L_3 \) (line \( AB \)).

This is confirmed algebraically by checking the sign of the expressions:

• \( L_1(\alpha, \beta) \times L_1(x_1, y_1) > 0 \)
• \( L_2(\alpha, \beta) \times L_2(x_2, y_2) > 0 \)
• \( L_3(\alpha, \beta) \times L_3(x_3, y_3) > 0 \)

If all these conditions are satisfied, then \( P(\alpha, \beta) \) lies inside \( \triangle ABC \).

Example

Does the point \( P(1,2) \) lie inside the triangle \( ABC \), where \( A \) is at \( (0,3) \), \( B \) is at \( (5,-4) \), and \( C \) is at \((-2,0)\)?

Solution:

First, we find the equations of the sides of the triangle \( ABC \):

• Equation of AB:

  \( \frac{y - 3}{x - 0} = \frac{-4 - 3}{5 - 0} \) simplifies to \( y - 3 = -\frac{7}{5}x \). Multiplying through by 5 gives \( 5y = -7x + 15 \) or \( 7x + 5y - 15 = 0 \).

• Equation of BC:

  \( \frac{y + 4}{x - 5} = \frac{0 + 4}{-2 - 5} \) simplifies to \( y + 4 = -\frac{4}{7}(x - 5) \). Clearing the fraction by multiplying through by 7 gives \( 7y = -4x + 20 + 28 \) or \( 4x + 7y + 8 = 0 \).

• Equation of CA:

  \( \frac{y - 0}{x + 2} = \frac{3 - 0}{0 + 2} \) simplifies to \( y = \frac{3}{2}(x + 2) \). Multiplying through by 2 gives \( 2y = 3x + 6 \) or \( 3x - 2y + 6 = 0 \).

To check if \( P \) lies inside \( \triangle ABC \), we evaluate the sign of the expressions:

• For line BC (4x + 7y + 8 = 0):

  Substituting \( P(1,2) \) gives \( 4(1) + 7(2) + 8 = 26 \) (positive),

  Substituting \( A(0,3) \) gives \( 4(0) + 7(3) + 8 = 29 \) (positive), indicating \( P \) and \( A \) are on the same side of \( BC \).

• For line CA (3x - 2y + 6 = 0):

  Substituting \( P(1,2) \) gives \( 3(1) - 2(2) + 6 = 5 \) (positive),

  Substituting \( B(5,-4) \) gives \( 3(5) - 2(-4) + 6 = 29 \) (positive), indicating \( P \) and \( B \) are on the same side of \( CA \).

• For line AB (7x + 5y - 15 = 0):

  Substituting \( P(1,2) \) gives \( 7(1) + 5(2) - 15 = 2 \) (positive),

  Substituting \( C(-2,0) \) gives \( 7(-2) + 5(0) - 15 = -29 \) (negative), indicating \( P \) and \( C \) are on opposite sides of \( AB \).

Conclusion: Since \( P \) does not satisfy the condition of being on the same side as the vertices across each corresponding side of the triangle, \( P \) does not lie inside the triangle \( ABC \).

Alternative Method using area of triangles

To determine whether a point \( P(\alpha, \beta) \) lies inside a triangle formed by the vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \), we can use the area method. This method involves calculating the areas of the sub-triangles formed by the point \( P \) and the vertices of the triangle.

1. Calculate the Area of the Triangle \( \Delta ABC \)

   The area of the triangle \( \Delta ABC \) can be found using the determinant formula:

   \[ \text{Area}_{ABC} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]

2. Calculate the Area of the Triangle \( \Delta PBC \)

   Similarly, the area of the triangle \( \Delta PBC \) is given by:

   \[ \text{Area}_{PBC} = \frac{1}{2} \left| \alpha(y_2 - y_3) + x_2(y_3 - \beta) + x_3(\beta - y_2) \right| \]

3. Calculate the Area of the Triangle \( \Delta PCA \)

   The area of the triangle \( \Delta PCA \) is:

   \[ \text{Area}_{PCA} = \frac{1}{2} \left| x_1(\beta - y_3) + \alpha(y_3 - y_1) + x_3(y_1 - \beta) \right| \]

4. Calculate the Area of the Triangle \( \Delta PAB \)

   The area of the triangle \( \Delta PAB \) is:

   \[ \text{Area}_{PAB} = \frac{1}{2} \left| x_1(y_2 - \beta) + x_2(\beta - y_1) + \alpha(y_1 - y_2) \right| \]

5. Sum of the Areas of Sub-Triangles

   Calculate the sum of the areas of the sub-triangles \( \Delta PBC \), \( \Delta PCA \), and \( \Delta PAB \):

   \[ \text{Sum of Sub-Triangle Areas} = \text{Area}_{PBC} + \text{Area}_{PCA} + \text{Area}_{PAB} \]

6. Compare with the Area of \( \Delta ABC \)

   If the sum of the areas of the sub-triangles is equal to the area of the main triangle \( \Delta ABC \), then the point \( P \) lies inside the triangle. Mathematically:

   \[ \text{Area}_{ABC} = \text{Area}_{PBC} + \text{Area}_{PCA} + \text{Area}_{PAB} \]