Pair of Angle Bisectors

Equation of Pair of Angular Bisectors:

Consider the pair of straight lines given by \( ax^2 + 2hxy + by^2 = 0 \). We aim to find the joint equation of the pair of angle bisectors of these lines.

Let \( y = m_1x \) and \( y = m_2x \) be the lines represented by the equation \( ax^2 + 2hxy + by^2 = 0 \).

We know that:

\[ m_1 + m_2 = -\frac{2h}{b} \quad \text{and} \quad m_1m_2 = \frac{a}{b} \]

Further, let \( \alpha_1 \) and \( \alpha_2 \) be the angles made by \( y = m_1x \) and \( y = m_2x \) with the x-axis. Thus,

\[ \tan \alpha_1 = m_1 \quad \text{and} \quad \tan \alpha_2 = m_2 \]

Observe that the bisector \( B_1 \) makes an angle \(\frac{\alpha_1 + \alpha_2}{2}\) with the x-axis, and bisector \( B_2 \) makes an angle \(\frac{\pi}{2} + \frac{\alpha_1 + \alpha_2}{2}\) with the x-axis. Thus,

\[ m_{B_1} = \tan \left( \frac{\alpha_1 + \alpha_2}{2} \right) \quad \text{and} \quad m_{B_2} = \tan \left( \frac{\pi}{2} + \frac{\alpha_1 + \alpha_2}{2} \right) = -\cot \left( \frac{\alpha_1 + \alpha_2}{2} \right) \]

Therefore, the equations of the angular bisectors are:

\[ y = \tan \left( \frac{\alpha_1 + \alpha_2}{2} \right)x \quad \text{and} \quad y = -\cot \left( \frac{\alpha_1 + \alpha_2}{2} \right)x \]

The corresponding joint equation is:

\[ \left[ y - \tan \left( \frac{\alpha_1 + \alpha_2}{2} \right)x \right] \left[ y + \cot \left( \frac{\alpha_1 + \alpha_2}{2} \right)x \right] = 0 \]

Expanding and simplifying:

\[ \begin{align*} y^2 + \left( \cot \left( \frac{\alpha_1 + \alpha_2}{2} \right) - \tan \left( \frac{\alpha_1 + \alpha_2}{2} \right) \right)xy - x^2 &= 0 \\ \text{Using the identity } \cot \theta - \tan \theta = 2 \cot 2\theta:& \\ y^2 + 2 \cot \left( \alpha_1 + \alpha_2 \right) xy - x^2 &= 0 \\ \text{Substituting } \alpha_1 \text{ and } \alpha_2 \text{ with } m_1 \text{ and } m_2:& \\ y^2 + 2 \left( \frac{1 - \tan \alpha_1 \tan \alpha_2}{\tan \alpha_1 + \tan \alpha_2} \right) xy - x^2 &= 0 \\ y^2 + 2 \left( \frac{1 - m_1 m_2}{m_1 + m_2} \right) xy - x^2 &= 0 \\ y^2 + 2 \left( \frac{1 - \frac{a}{b}}{-\frac{2h}{b}} \right) xy - x^2 &= 0 \\ y^2 + \frac{2(b - a)}{-2h} xy - x^2 &= 0 \\ y^2 - \frac{a - b}{h} xy - x^2 &= 0 \\ \text{Multiplying through by } h:& \\ h (y^2 - x^2) &= (a - b) xy \end{align*} \]

Therefore, the joint equation of the pair of angular bisectors is:

\[ \boxed{h(x^2 - y^2) = (a - b)xy} \]

Example

Find the pair of angle bisectors for the equation \( 2x^2 - 3xy - 4y^2 = 0 \).

Solution:

Given the equation \( 2x^2 - 3xy - 4y^2 = 0 \), we need to find the equation of the pair of angle bisectors.

We have the general form of the joint equation of the angle bisectors as:

\[ h(x^2 - y^2) = (a - b)xy \]

For our given equation, \( a = 2 \), \( b = -4 \), and \( 2h = -3 \). Therefore, \( h = -\frac{3}{2} \).

Using the formula and substituting the values, we get:

\[ \begin{align*} h(x^2 - y^2) &= (a - b)xy \\ -\frac{3}{2}(x^2 - y^2) &= (2 + 4)xy \\ -\frac{3}{2}(x^2 - y^2) &= 6xy \\ 3(x^2 - y^2) &= -12xy \\ x^2 - y^2 &= -4xy \\ \end{align*} \]

Therefore, the equation of the pair of angle bisectors is:

\[ \boxed{x^2 - y^2 + 4xy = 0} \]

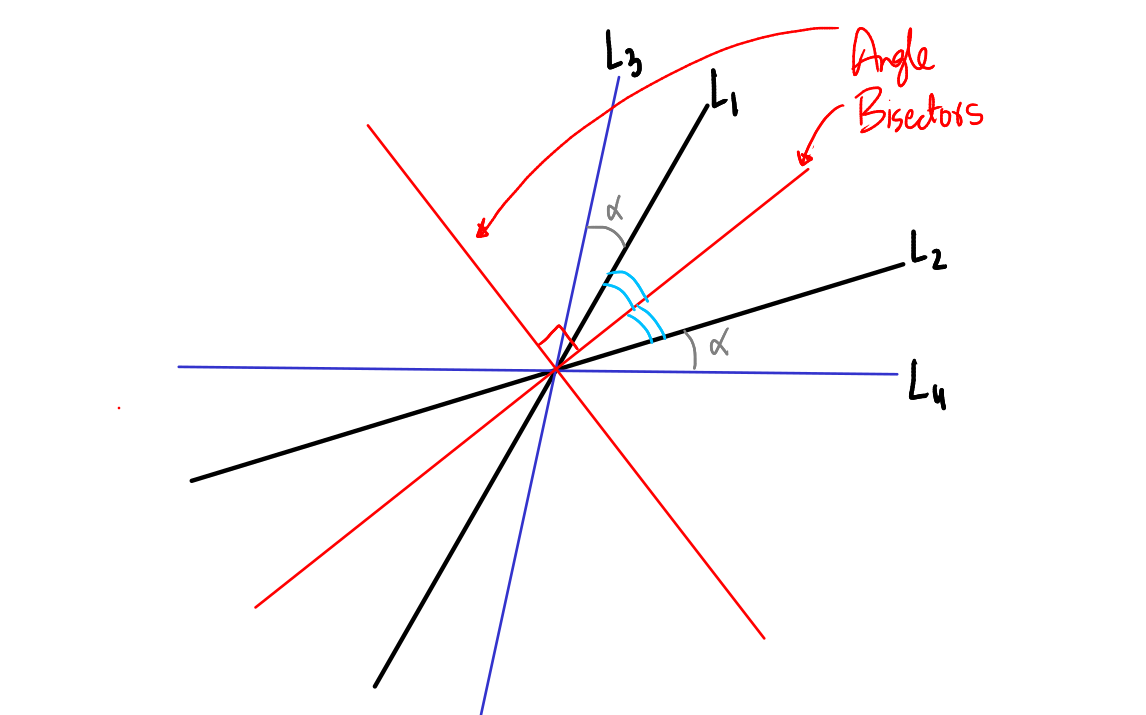
Equal Inclination of a Pair of Straight Lines with other stuff

Two pairs of straight lines are equally inclined with each other if they have the same pair of angle bisectors.

To support this statement, consider two pairs of straight lines \( L_1L_2: a_1x^2 + 2h_1xy + b_1y^2 = 0 \) and \( L_3L_4: a_2x^2 + 2h_2xy + b_2y^2 = 0 \).

If \( L_1 \) and \( L_3 \) make the same angle with each other as \( L_2 \) and \( L_4 \), then we say they are equally inclined to each other. In that case, the geometry confirms that their angle bisectors are the same.

For the first pair, the equation of the angle bisectors is:

\[ h_1(x^2 - y^2) = (a_1 - b_1)xy \]

For the second pair, the equation of the angle bisectors is:

\[ h_2(x^2 - y^2) = (a_2 - b_2)xy \]

Since both represent the same pair of angle bisectors, we have:

\[ \frac{h_1}{h_2} = \frac{(a_1 - b_1)}{(a_2 - b_2)} \]

Therefore, if two pairs of straight lines are equally inclined, their angle bisectors are the same, and this relationship holds:

\[ \boxed{\frac{h_1}{h_2} = \frac{(a_1 - b_1)}{(a_2 - b_2)}} \]

Example

Consider the two pairs of straight lines given by the equations \( 2x^2 - 3xy - y^2 = 0 \) and \( x^2 - 6xy - 5y^2 = 0 \).

To determine if these pairs of straight lines are equally inclined to each other, we use the condition for equally inclined lines:

\[ \frac{h_1}{h_2} = \frac{(a_1 - b_1)}{(a_2 - b_2)} \]

For the first equation, we have:

\[ a_1 = 2, \; b_1 = -1, \; 2h_1 = -3 \Rightarrow h_1 = -\frac{3}{2} \]

For the second equation, we have:

\[ a_2 = 1, \; b_2 = -5, \; 2h_2 = -6 \Rightarrow h_2 = -3 \]

Now, check the condition:

\[ \frac{h_1}{h_2} = \frac{-\frac{3}{2}}{-3} = \frac{1}{2} \]

\[ \frac{(a_1 - b_1)}{(a_2 - b_2)} = \frac{2 - (-1)}{1 - (-5)} = \frac{3}{6} = \frac{1}{2} \]

Both ratios are equal, confirming that the pairs of straight lines \( 2x^2 - 3xy - y^2 = 0 \) and \( x^2 - 6xy - 5y^2 = 0 \) are equally inclined.