Triangles and Pair of Straight Lines

Triangles formed by a pair of lines with another line

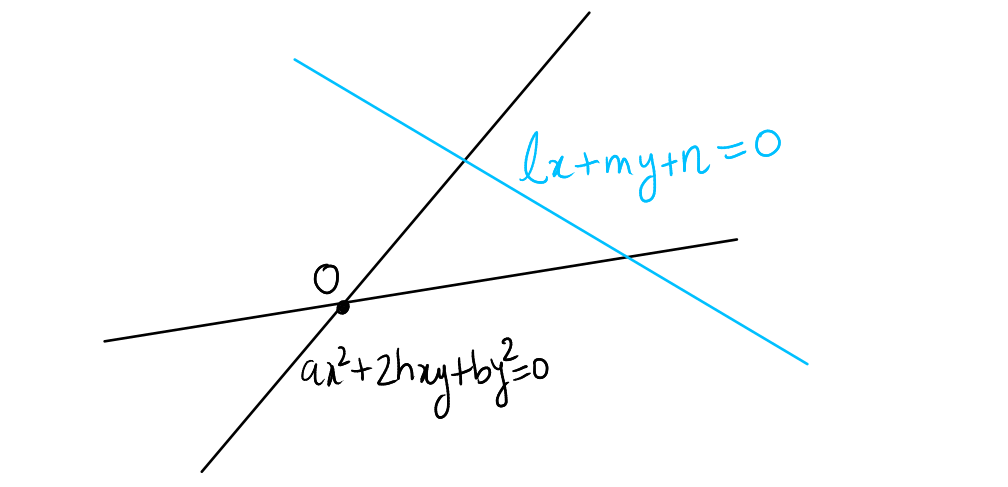
Consider a pair of straight lines \( ax^2 + 2hxy + by^2 = 0 \) and a line \( lx + my + n = 0 \). They intersect at two points, \( A \) and \( B \). We are interested in the nature of \( \Delta OAB \).

The triangle \( \Delta OAB \) formed by the lines represented by \( ax^2 + 2hxy + by^2 = 0 \) and a line \( lx + my + n = 0 \) is isosceles if \( h(l^2 - m^2) = (a - b)lm \).

Proof:

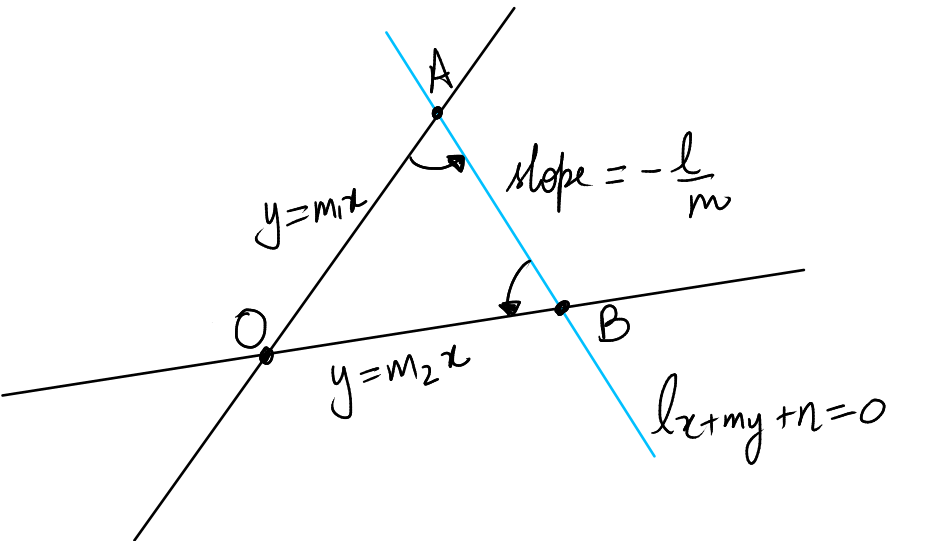
Let \( y = m_1x \) and \( y = m_2x \) be lines represented by \( ax^2 + 2hxy + by^2 = 0 \).

\[ m_1 + m_2 = -\frac{2h}{b} \]

\[ m_1m_2 = \frac{a}{b} \]

Slope of line \( AB \) is \(-\frac{l}{m} \).

Since \( \angle OAB = \angle OBA \):

\[ \tan \angle OAB = \tan \angle OBA \]

\[ \implies \frac{-\frac{l}{m} - m_1}{1 + \frac{l}{m} m_1} = \frac{m_2 + \frac{l}{m}}{1 - \frac{l}{m} m_2} \]

\[ \implies \frac{-l - mm_1}{m + lm_1} = \frac{m_2m + l}{m - lm_2} \]

\[ \implies (l + mm_1)(m - lm_2) = (lm_1 - m)(l + mm_2) \]

\[ \implies lm - l^2m_2 + m^2m_1 - mm_1lm_2 = l^2m_1 + lm_1m_2 - m^2m_2 \]

\[ \implies 2lm = 2lm m_1m_2 + l^2(m_1 - m_2) - m^2(m_1 - m_2) \]

Substituting \( m_1 + m_2 = -\frac{2h}{b} \) and \( m_1m_2 = \frac{a}{b} \):

\[ \implies 2lm = 2lm \frac{a}{b} - (l^2 - m^2)\frac{2h}{b} \]

\[ \implies 2lmb = 2lma - (l^2 - m^2)2h \]

\[ \implies lmb = lma - (l^2 - m^2)h \]

\[ \implies (l^2 - m^2)h = lm(a - b) \]

Therefore, the triangle \( \Delta OAB \) is isosceles if:

\[ \boxed{h(l^2 - m^2) = (a - b)lm} \]

This completes the proof.

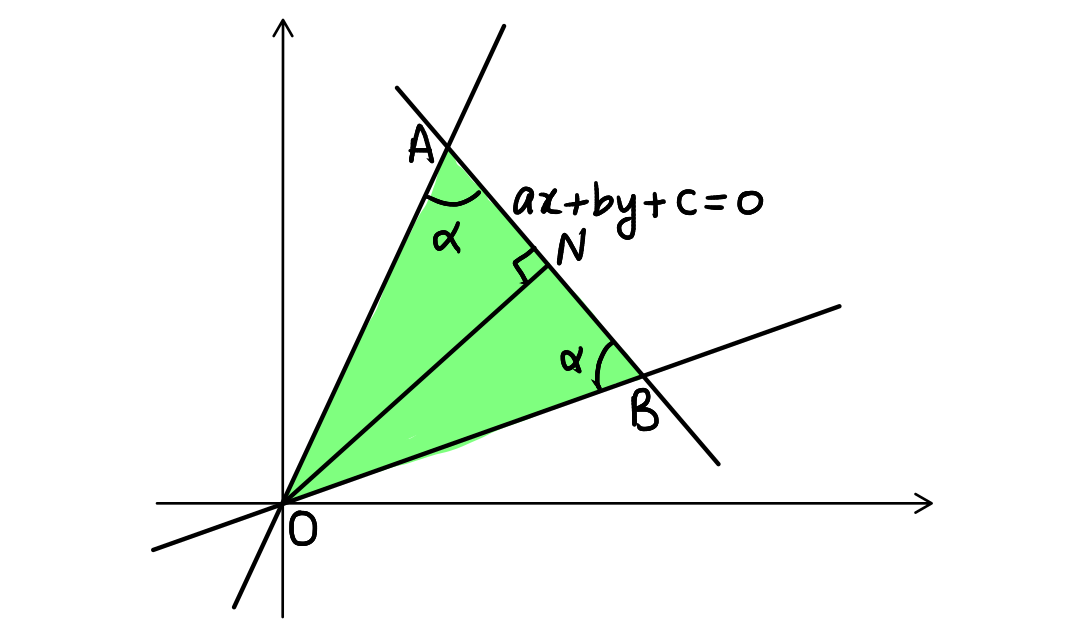
Consider a straight line \( ax + by + c = 0 \). We wish to find a pair of straight lines passing through the origin and forming an isosceles triangle with \( ax + by + c = 0 \) as the base, where the vertex angle is \( \alpha \).

Theorem: The equation of a pair of straight lines passing through the origin and forming an isosceles triangle with a given line \( ax + by + c = 0 \) as the base, where the vertex angle is \( \alpha \), is \( (ax + by)^2 - \tan^2 \alpha (bx - ay)^2 = 0 \).

Proof:

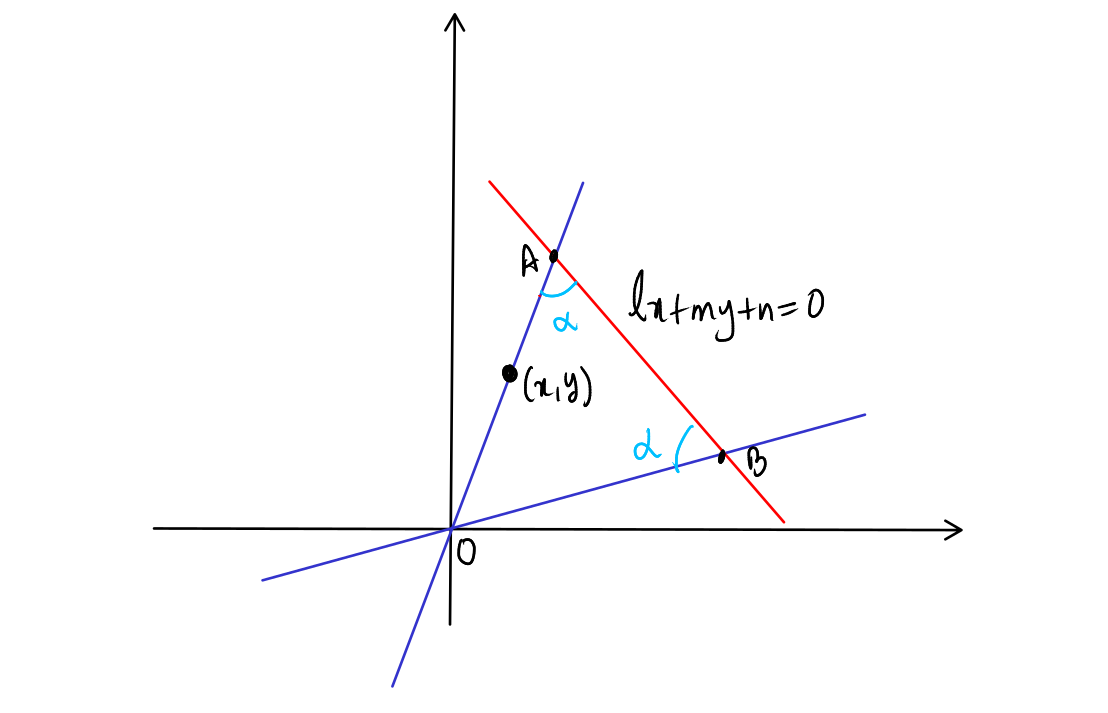
Let the lines \( OA \) and \( OB \) be represented as shown in the figure. Let \((x, y)\) be a point on \( OA \). The slope of \( OA \) is \( \frac{y}{x} \).

The slope of the line \( ax + by + c = 0 \) is \( -\frac{a}{b} \).

Given that \( \angle OAB = \alpha \):

\[ \tan \alpha = \left| \frac{-\frac{a}{b} - \frac{y}{x}}{1 + \frac{a}{b} \frac{y}{x}} \right| = \left| \frac{ax + by}{bx - ay} \right| \]

\[ \implies \tan^2 \alpha = \left( \frac{ax + by}{bx - ay} \right)^2 \]

\[ \implies (ax + by)^2 - \tan^2 \alpha (bx - ay)^2 = 0 \]

Therefore, the equation of the pair of lines is:

\[ \boxed{(ax + by)^2 - \tan^2 \alpha (bx - ay)^2 = 0} \]

This completes the proof.

Special Cases:

1. If \( \alpha = 60^\circ \):

   • The triangle formed is equilateral.
   • The equation becomes:
   \[ (ax + by)^2 - 3(bx - ay)^2 = 0 \]

2. If \( \alpha = 45^\circ \):

   • The triangle formed is a right-angled isosceles triangle.
   • The equation becomes:
   \[ (ax + by)^2 - (bx - ay)^2 = 0 \]

A pair of straight lines \( ax^2 + 2hxy + by^2 = 0 \) forms an equilateral triangle with the line \( lx + my + n = 0 \) if it can be expressed as:

\[ (lx + my)^2 - 3(mx - ly)^2 = 0 \]

e.g. The pair of straight lines \(3x^2 + 48xy + 23y^2 = 0\), and the line is \(3x - 2y + 4 = 0\) form an equilateral triangleWe can show this by expressing it as \((3x - 2y)^2 - 3(2x + 3y)^2 = 0\). Observe that

\[ (3x - 2y)^2 - 3(2x + 3y)^2 = 0 \]

\[ \implies \begin{align*} (3x - 2y)^2 - 3(2x + 3y)^2 & = (9x^2 - 12xy + 4y^2) - 3(4x^2 + 12xy + 9y^2) \\ & = 9x^2 - 12xy + 4y^2 - (12x^2 + 36xy + 27y^2) \\ & = (9x^2 - 12x^2) + (-12xy - 36xy) + (4y^2 - 27y^2) \\ & = -3x^2 - 48xy - 23y^2 \end{align*} \]

Thus,

\[ (3x - 2y)^2 - 3(2x + 3y)^2 = 0 \implies -3x^2 - 48xy - 23y^2 = 0 \]

which simplifies to:

\[ 3x^2 + 48xy + 23y^2 = 0 \]

Therefore, the pair of straight lines \(3x^2 + 48xy + 23y^2 = 0\) and the line \(3x - 2y + 4 = 0\) form an equilateral triangle because the given pair of lines can be expressed as \((3x - 2y)^2 - 3(2x + 3y)^2 = 0\).

A line \(lx + my + n = 0\) forms a right-angled triangle with \(ax^2 + 2hxy + by^2 = 0\) if \(a + b = 0\) or \(al^2 + 2hlm + bm^2 = 0\).

Proof:

We know that the angle between a pair of lines is a right angle if \(a + b = 0\). Thus, whatever the line \(lx + my + n = 0\), if it is not parallel to a line in the pair, then we always get a right-angled triangle.

A right-angled triangle can also be obtained if the line \(lx + my + n = 0\) is perpendicular to one of the lines of \(ax^2 + 2hxy + by^2 = 0\).

Let \(y = m_1x\) and \(y = m_2x\) be lines represented by \(ax^2 + 2hxy + by^2 = 0\).

Let \(lx + my + n = 0\) be perpendicular to \(y = m_1x\).

Then:

\[ -\frac{l}{m} \cdot m_1 = -1 \implies m_1 = \frac{m}{l} \]

We know that:

\[ a + 2hm_1 + bm_1^2 = 0 \]

\[ \implies a + 2h\left(\frac{m}{l}\right) + b\left(\frac{m}{l}\right)^2 = 0 \]

\[ \implies a + \frac{2hm}{l} + \frac{bm^2}{l^2} = 0 \]

\[ \implies al^2 + 2hlm + bm^2 = 0 \]

Hence, a line \(lx + my + n = 0\) forms a right-angled triangle with \(ax^2 + 2hxy + by^2 = 0\) if:

\[ \boxed{a + b = 0 \text{ or } al^2 + 2hlm + bm^2 = 0} \]

Area of Triangles formed by a pair of straight lines with a given straight line

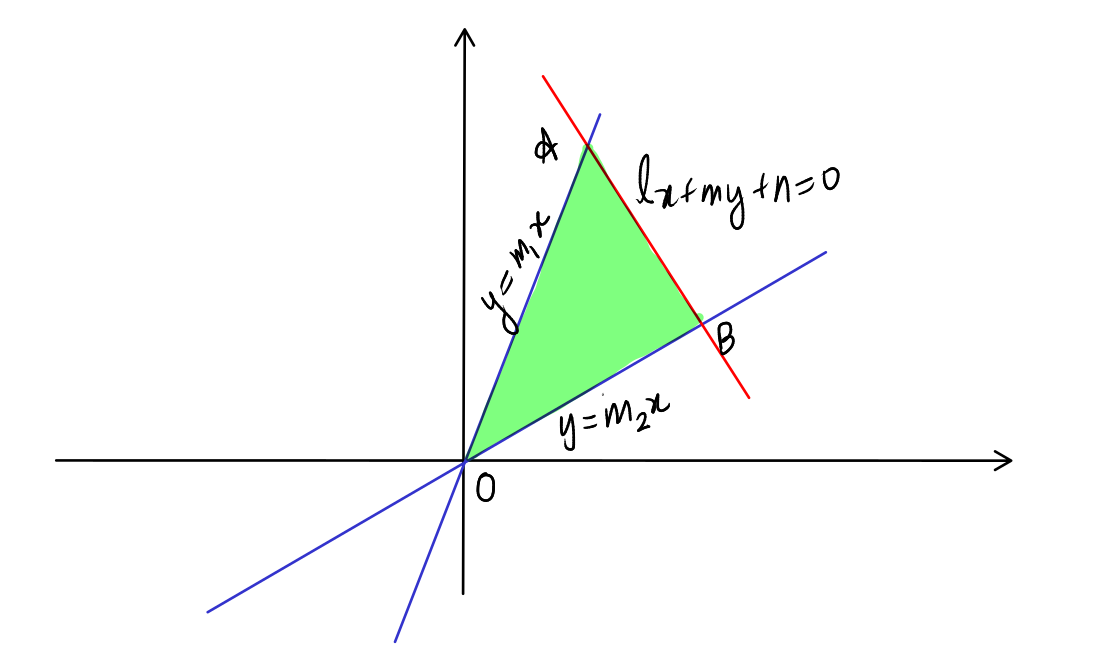
Consider the triangle formed by a pair of straight lines \( ax^2 + 2hxy + by^2 = 0 \) and the line \( lx + my + n = 0 \). We wish to find the area of this triangle.

Let \( y = m_1x \) and \( y = m_2x \) be the lines represented by \( ax^2 + 2hxy + by^2 = 0 \).

\[ m_1 + m_2 = -\frac{2h}{b} \quad \text{and} \quad m_1m_2 = \frac{a}{b} \]

Let \( A \) and \( B \) be the intersection points of \( lx + my + n = 0 \) with \( y = m_1x \) and \( y = m_2x \), respectively. First, we find \( A \) and \( B \).

For \( A \):

\[ lx + mm_1x + n = 0 \implies x = \frac{-n}{l + mm_1}, \quad y = \frac{-nm_1}{l + mm_1} \]

Therefore, \( A \) is:

\[ A \left( \frac{-n}{l + mm_1}, \frac{-nm_1}{l + mm_1} \right) \]

Similarly, for \( B \):

\[ B \left( \frac{-n}{l + mm_2}, \frac{-nm_2}{l + mm_2} \right) \]

The area of \( \Delta OAB \) is given by:

\[ \text{Area} = \frac{1}{2} \left| x_A y_B - x_B y_A \right| \]

Substituting the coordinates:

\[ \text{Area} = \frac{1}{2} \left| \frac{-n}{l + mm_1} \cdot \frac{-nm_2}{l + mm_2} - \frac{-n}{l + mm_2} \cdot \frac{-nm_1}{l + mm_1} \right| \]

\[ = \frac{1}{2} \left| \frac{n^2 m_2}{(l + mm_1)(l + mm_2)} - \frac{n^2 m_1}{(l + mm_2)(l + mm_1)} \right| \]

\[ = \frac{n^2}{2} \left| \frac{m_2 - m_1}{(l + mm_1)(l + mm_2)} \right| \]

\[ = \frac{n^2}{2} \left| \frac{\sqrt{\left( \frac{-2h}{b} \right)^2 - 4 \left( \frac{a}{b} \right)}}{l^2 + lm \left( -\frac{2h}{b} \right) + m^2 \left( \frac{a}{b} \right)} \right| \]

\[ = \frac{n^2}{2} \left| \frac{\sqrt{\frac{4h^2}{b^2} - \frac{4a}{b}}}{l^2 - \frac{2hlm}{b} + \frac{a m^2}{b}} \right| \]

\[ = \frac{n^2}{2} \left| \frac{2 \sqrt{h^2 - ab}}{b \left( l^2 - \frac{2hlm}{b} + \frac{a m^2}{b} \right)} \right| \]

\[ = \frac{n^2 \sqrt{h^2 - ab}}{ \left| b \left( l^2 - \frac{2hlm}{b} + \frac{a m^2}{b} \right) \right|} \]

\[ = \frac{n^2 \sqrt{h^2 - ab}}{ \left| bl^2 - 2hlm + am^2 \right|} \]

Therefore, the area of the triangle is:

\[ \boxed{\text{Area} = \frac{n^2 \sqrt{h^2 - ab}}{ \left| bl^2 - 2hlm + am^2 \right|}} \]

Area of isosceles triangle formed by a line with a pair of striaght lines

Consider a straight line \( ax + by + c = 0 \) and a pair of straight lines passing through the origin, forming an isosceles triangle with the base as \( ax + by + c = 0 \) and base angle \(\alpha\). We know that the equation of the pair of straight lines is:

\[ (ax + by)^2 - \tan^2 \alpha (bx - ay)^2 = 0 \]

We are now interested in finding the area of this isosceles triangle.

First, we need to calculate the altitude \( ON \) of \( \Delta OAB \). This is the perpendicular distance from the origin \( O \) to the line \( AB \), which is the base of the triangle.

\[ ON = \text{perpendicular distance of origin O from the line } AB \]

\[ ON = \frac{|c|}{\sqrt{a^2 + b^2}} \]

Next, we calculate \( AN \), which is the segment of the altitude from point \( A \) (one end of the base) to the point \( N \) (where the altitude intersects the base). Given that \( \angle OAN = \alpha \), we use the relationship between the altitude and the base angle:

\[ AN = ON \cot \alpha \]

Since the triangle is isosceles, the base \( AB \) can be expressed as twice the length of \( AN \):

\[ AB = 2AN = 2ON \cot \alpha \]

Now, we can calculate the area of \( \Delta OAB \). The area of a triangle is given by half the product of its base and height:

\[ \text{Area of } \Delta OAB = \frac{1}{2} \times AB \times ON \]

Substituting the expressions for \( AB \) and \( ON \):

\[ \text{Area of } \Delta OAB = \frac{1}{2} \times 2ON \cot \alpha \times ON \]

\[ = ON^2 \cot \alpha \]

Substituting the value of \( ON \):

\[ ON = \frac{|c|}{\sqrt{a^2 + b^2}} \]

Thus:

\[ \text{Area} = \left( \frac{|c|}{\sqrt{a^2 + b^2}} \right)^2 \cot \alpha \]

\[ = \frac{c^2 \cot \alpha}{a^2 + b^2} \]

\[ = \frac{c^2}{\tan \alpha (a^2 + b^2)} \]

Therefore, the area of the isosceles triangle formed by the pair of straight lines \( (ax + by)^2 - \tan^2 \alpha (bx - ay)^2 = 0 \) and the line \( ax + by + c = 0 \) is:

\[ \boxed{\text{Area} = \frac{c^2}{\tan \alpha (a^2 + b^2)}} \]