3 Venn Diagrams

Venn diagrams are an instrumental tool for visually representing sets and their relationships. These diagrams typically depict the universal set as a rectangle encompassing all other sets.

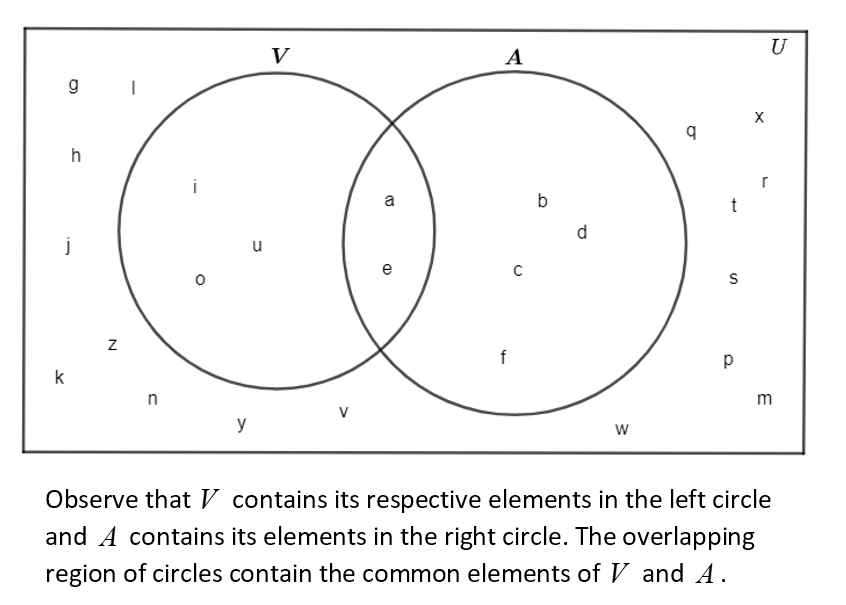
For clarity, consider the universal set \( U \) as the comprehensive collection of all objects within the scope of discussion. For instance, if we designate set \( V \) as \( \{a, e, i, o, u\} \) and set \( A \) as \( \{a, b, c, d, e, f\} \), and all objects in question are letters of the alphabet, then the universal set \( U \) could be defined as \( \{a, b, c, d, \ldots, x, y, z\} \).

In a Venn diagram, the universal set \( U \) is depicted by a rectangle, while individual sets such as \( A \) and \( V \) are represented by shapes like circles or ellipses within the rectangle, each containing their unique elements.

From the provided diagram, we observe that set \( V \) is symbolized by the left circle, containing its elements, while set \( A \) is symbolized by the right circle. The intersecting region between the two circles represents the common elements shared by sets \( V \) and \( A \).