Circular Trigonometric Functions
Definition
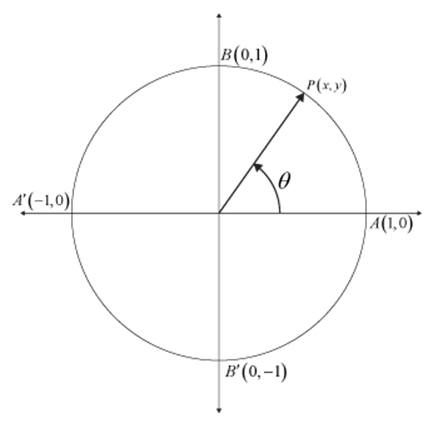
Let there be a unit circle (a circle of radius 1 unit) in the cartesian coordinate system such that the centre of the circle is at the origin. Let \( \theta \) be any angle such that its terminal point is \( P (x,y) \).
-
\( \theta \) is a standard angle measured from positive axis.
-
This circle cuts the axes at \( A(1,0) \), \( B(0,1) \), \( A'(-1,0) \) and \( B'(0,-1) \). Thus, for any point \( P (x,y) \) on this circle, \( -1 \leq x \leq 1 \) and \( -1 \leq y \leq 1 \).
This is how we define trigonometric functions.
SINE of angle \( \theta \) is defined to be equal to \( y \) (the ordinate of point \( P \))
COSINE of angle \( \theta \) is defined to be equal to \( x \) (the abscissa of point \( P \))
TANGENT of angle \( \theta \) is defined to be equal to \( \frac{y}{x} \) (the ratio of ordinate to abscissa)
Reciprocal trigonometric functions:
The reciprocal of sine is said to be cosecant.
COSECANT of angle \( \theta \) is equal to \( \frac{1}{y} \)
SECANT of angle \( \theta \) is equal to \( \frac{1}{x} \)
COTANGENT of angle \( \theta \) is equal to \( \frac{x}{y} \)
That’s it. This is how the circular trigonometric functions are defined.
What happened to old definitions of sine, cosine and tangent?
Is \( \sin 60^\circ \) still equal to \( \frac{\sqrt{3}}{2} \)?
The old definition of sine, cosine and tangent, where we called them as trigonometric ratios in contrast to what we are calling them now – trigonometric functions, involved a right-angled triangle. We defined trigonometric ratios as ratios of sides of the triangle. At first this new definition feels quite strange. Are those identities like \( \sin^2 \theta + \cos^2 \theta = 1 \) etc still valid?
- This new definition of TRIGONOMETRIC FUNCTIONS defined on an unit circle is an extension to the old definition of TRIGONOMETRIC RATIOS defined on a right-angled triangle.
Everything from the old definition is still valid. Because of this new definition though we get some new and interesting results.
- In the old definition sin 120° was not defined. But in the new definition it is equal to \( \frac{1}{2} \). We will see why it is so in a while. Actually, now, trigonometric functions are defined for any angle (because of division involved in the definition, it may not be so for some angles). We will see that now something like cos (−90°) is defined (and is equal to 0).
Why is the new definition an extension to the old definition?
The old definition was only valid for angles between 0° and 90° (inclusive). If observed carefully, we see when the angle \( \theta \) is between 0° and 90°, then \( \theta \) lies in the first quadrant. From the terminal point \( P \) of the angle \( \theta \) drop a perpendicular to the \( x \)-axis and let its foot be \( N \). Observe that \( PN = y \), \( ON = x \) and \( OP = 1 \) unit.
\( \triangle OPN \) is a right-angled triangle where angle \( NOP \) is equal to \( \theta \). In this right-angled triangle, using the old definitions we see that
Which according to the new definition are the same values. Thus, we reach this conclusion that the new definition does not defy the old definition and is in fact an extension to the old definition with some new properties that we will study in detail in a while.
sin120°, cos120° and tan120°
To understand how to use this new definition we start with calculation of values of trigonometric
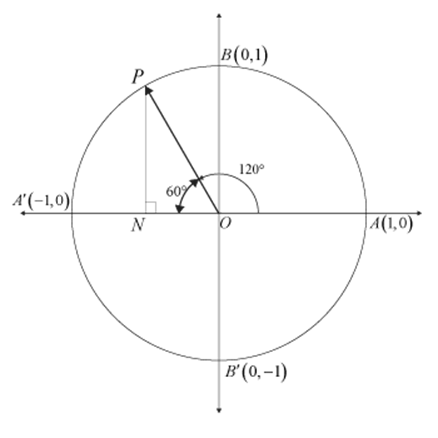
We construct the angle 120° and “somehow” calculate the coordinate of its terminal point. That’s it, we will be done!
Let us construct this angle on the unit circle.
P is the terminal point of the angle 120°. We wish to calculate the coordinates of P. To do that let us drop a perpendicular from point P to the x-axis. In \( \triangle OPN \), the angle \( NOP \) is equal to 60°. Using right hand trigonometry, we calculate \( ON = OP \cos 60° = \frac{1}{2} \) and \( PN = OP \sin 60° = \frac{\sqrt{3}}{2} \).
Thus, the coordinates of point P are \( \left( -\frac{1}{2}, \frac{\sqrt{3}}{2} \right) \).
According to the definition of circular trigonometric functions,
\( \sin 120° = \text{ordinate of point P} = \frac{\sqrt{3}}{2} \) and \( \cos 120° = \text{abscissa of point P} = -\frac{1}{2} \)
Similarly, \( \tan 120° = \frac{\text{ordinate}}{\text{abscissa}} = \frac{\frac{\sqrt{3}}{2}}{-\frac{1}{2}} = -\sqrt{3} \)
Let us take one more example. For the angle \( \theta = -120° \), let us calculate values of trigonometric functions.
Draw \( \theta = -120° \) on the unit circle. Let P be the terminal point. Drop a perpendicular from point P to the x-axis. In the right-angled triangle \( OPN \), \( \angle NOP = 60° \). Using right-angled triangle trigonometry, \( ON = OP \cos 60^\circ = -\frac{1}{2} \) and \( PN = OP \sin 60^\circ = \frac{\sqrt{3}}{2} \). Thus the coordinates of \( P \) are \( \left( -\frac{1}{2}, -\frac{\sqrt{3}}{2} \right) \).
Therefore, \( \sin(-120^\circ) = -\frac{\sqrt{3}}{2} \), \( \cos(-120^\circ) = -\frac{1}{2} \) and \( \tan(-120^\circ) = \sqrt{3} \)
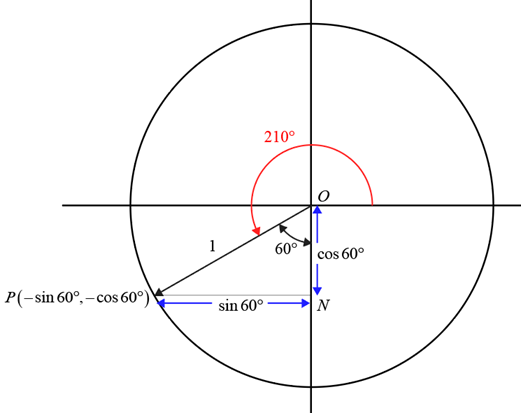
To practice more let us calculate values of trigonometric functions for \( 210^\circ \)
Construct 210°. Terminal point \( P \) lies in the third quadrant. We want to find out coordinates of \( P \). To do that let us draw a normal \( PN \) from point \( P \) to y axis. We get a right-angled triangle \( OPN \). Clearly angle \( PON \) is 60°. Using right angles trigonometry sin 60° = \( \frac{PN}{ON} = \frac{PN}{1} = PN \)
\(\Rightarrow PN = \sin 60° = \frac{\sqrt{3}}{2} \) and \( ON = \cos 60° = -\frac{1}{2} \). Thus, coordinates of \( P \) are \( \left( -\frac{\sqrt{3}}{2}, -\frac{1}{2} \right) \).
Therefore, by definitions of trigonometric functions,
Sign of Trigonometric Functions
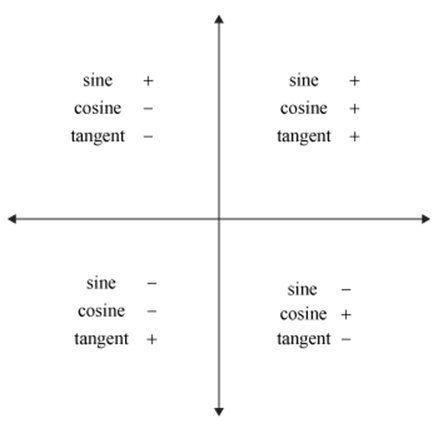
Since, sine of an angle is equal to the ordinate of its terminal point, the value of sine must be positive in the first and the second quadrant and negative in the third and fourth quadrant. Similarly cosine, being equal to abscissa, is positive in first and fourth quadrant and negative in the second and the third quadrant. Tangent, on the other hand, is the ratio of ordinate to abscissa. It is positive when both ordinate and abscissa have same signs. Thus, tangent is positive in the first and the third quadrant, while it is negative in second and the fourth quadrant. Their reciprocal functions also have the corresponding signs.
Now let us learn how this process of calculating values of trigonometric functions for any angle can be made shorter and quicker.
Crux
Values of trigonometric functions for any angle can be related to values of trigonometric functions of some acute angle.
Let there be an angle \( \theta \). For some \( n \in \mathbb{Z} \), \( \theta = n\pi + \alpha \) such that \( \alpha \) is an acute angle. What we mean is this that you are given some angle and you are able to write that angle as a sum of a horizontal angle (multiple of \( \pi \) or 180°) and an acute angle. E.g., \( \frac{55\pi}{3} \) can be written as \( (54 + 1)\frac{\pi}{3} = 18\pi + \frac{\pi}{3} \). If the angle given in radians is of the form \( \frac{p\pi}{q} \), find the closest multiple of \( q \) to \( p \) and write \( p \) in terms of that multiple. We did the same in the example. 54 is the closest multiple of 3 to 55. Thus we wrote 55=54+1. And the rest is simple. If the angle is in degrees, for instance, 480°, we find the closest multiple of 180° to it, which is 540°, and then we write 480° = 540° - 60°.
Once you’ve done so, now decide the correct quadrant of the angle. With the quadrant of the angle, you should be able to determine the sign of the value. When this is done too, we have this simple rule.
Where \( T \) is any trigonometric function like sin, cosine etc.
In the decided quadrant of \( \theta \) decide whether the trigonometric function \( T \) is positive or negative.
e.g. \( \sin \frac{44\pi}{3} = \sin \left( \frac{45 - 1}{3} \pi \right) = \sin \left( \frac{15\pi - \frac{\pi}{3}}{3} \right) \)
\( \frac{44\pi}{3} = 15\pi - \frac{\pi}{3} \) lies in the second quadrant where sine is positive. Therefore,
Example
Find the value of
a) \( \sin 225^\circ \)
b) \( \cos \frac{99\pi}{4} \)
c) \( \sec \frac{11\pi}{3} \)
d) \( \cot 495^\circ \)
Solution: a) \( 225^\circ = 180^\circ + 45^\circ \)
This angle lies in the third quadrant where sine is negative. Thus,
\( \sin 225^\circ = \sin(180^\circ + 45^\circ) = -\sin 45^\circ = -\frac{1}{\sqrt{2}} \)
b) \( \frac{99\pi}{4} = (100 - 1) \frac{\pi}{4} = 25\pi - \frac{\pi}{4} \)
This angle lies in the second quadrant, where cosine is negative. Thus,
c) \( \frac{11\pi}{3} = (12 - 1)\frac{\pi}{3} = 4\pi - \frac{\pi}{3} \)
This angle lies in the fourth quadrant, where secant is positive.
Thus, \( \sec \left( \frac{11\pi}{3} \right) = \sec \left( 4\pi - \frac{\pi}{3} \right) = \sec \left( -\frac{\pi}{3} \right) = 2 \)
d) \( 495^\circ = 540^\circ - 45^\circ = 3 \times 180^\circ - 45^\circ \) which lies in the second quadrant. Cotangent is negative in that quadrant. Thus,
A point to be noted.
Now we said before that \( \alpha \) is acute, but that condition is not very necessary. Even if \( \alpha \) is not acute, we consider it to be acute while deciding the quadrant! Sounds confusing but it works.
e.g. What is the value of \( \cos 300^\circ \)?
Solution: \( 300^\circ = 360^\circ - 60^\circ = 2 \times 180^\circ - 60^\circ \) which lies in the fourth quadrant and cosine is positive there.
Thus, \( \cos 300^\circ = \cos (360^\circ - 60^\circ) = \cos 60^\circ = \frac{1}{2} \)
But if we write, \( \cos 300^\circ = \cos (180^\circ + 120^\circ) \)
Now \( 180^\circ + 120^\circ \) lies in the fourth quadrant. But to apply what we learned above, we consider \( 120^\circ \) to be acute and consider as if \( 180^\circ + 120^\circ \) lies in the third quadrant.
Thus, \( \cos (180^\circ + 120^\circ) = -\cos 120^\circ \) (because in the third quadrant cosine is negative, we have put the minus sign)
Now \( \cos 120^\circ = \cos (180^\circ - 60^\circ) \) (\( 180^\circ - 60^\circ \) actually lies in the second quadrant where cosine is negative)
Thus, \( \cos 300^\circ = -\cos 120^\circ = -\left( -\frac{1}{2} \right) = \frac{1}{2} \)
We get the same answer. You would think what is the point of doing so when we could have done easily using the former method. The only point we want to make is whether \( \alpha \) is acute or not, you consider it to be acute.
For example: \( \cos (5\pi - \alpha) = -\cos \alpha \) (we consider \( \alpha \) to be acute. Thus \( 5\pi - \alpha \) lies in the second quadrant where cosine is negative and thus we get \( -\cos \alpha \) )
You may remember the following results if you wish to:
-
\( -\theta \)
Since, \( -\theta = 0 - \theta \) (0 is a horizontal angle)
It lies in the fourth quadrant. Thus,
\[ \sin(-\theta) = -\sin \theta \]\[ \cos(-\theta) = \cos \theta \]\[ \tan(-\theta) = -\tan \theta \] -
\( \pi - \theta \)
Since, \( \pi - \theta \) lies in the second quadrant,
\[ \sin(\pi - \theta) = \sin \theta \]\[ \cos(\pi - \theta) = -\cos \theta \]\[ \tan(\pi - \theta) = -\tan \theta \] -
\( \pi + \theta \)
Since, \( \pi + \theta \) lies in the third quadrant,
\[ \sin(\pi + \theta) = -\sin \theta \]\[ \cos(\pi + \theta) = -\cos \theta \]\[ \tan(\pi + \theta) = \tan \theta \] -
\( 2\pi - \theta \)
Since, \( 2\pi - \theta \) lies in the fourth quadrant,
\[ \sin(2\pi - \theta) = -\sin \theta \]\[ \cos(2\pi - \theta) = \cos \theta \]\[ \tan(2\pi - \theta) = -\tan \theta \] -
\( 2\pi + \theta \)
Since, \( 2\pi + \theta \) lies in the first quadrant,
\[ \sin(2\pi + \theta) = \sin \theta \]\[ \cos(2\pi + \theta) = \cos \theta \]\[ \tan(2\pi + \theta) = \tan \theta \]
We have another rule which makes life easier.
Let there be an angle \( \theta \) which can be written as \( \theta = (2n+1)\frac{\pi}{2} + \alpha \) (Assuming \( \alpha \) to be acute and \( n \in \mathbb{Z} \))
We are writing \( \theta \) in terms of vertical angle \( \left(2n+1\right)\frac{\pi}{2} \).
If \( T \) represents some trigonometric function and \( T' \) is its complementary function.
What's a complementary function?
| Trigonometric Function | Complementary trigonometric function |
|---|---|
| sine | cosine |
| cosine | sine |
| Secant | Cosecant |
| cosecant | secant |
| tangent | cotangent |
| cotangent | tangent |
Now, \( T(\theta) = T(\text{vertical angle} \pm \theta) = (\pm \text{ or } - \text{ sign based on quadrant of } \theta)T'(\alpha) \)
For example, \( \cos(90^\circ + \theta) = -\sin \theta \). Why? Because \( 90^\circ + \theta \) lies in the second quadrant (we always assume that \( \theta \) is acute). Since \( 90^\circ \) is a vertical angle, cosine become sine and we put a minus sign because cosine is negative in the second quadrant.
Example
Find the value of \( \tan\left(\frac{7\pi}{2} - \frac{\pi}{3}\right) \).
Solution:
\( \frac{7\pi}{2} \) is a vertical angle whose terminal point lies on negative \( y \)-axis. Thus, \( \frac{7\pi}{2} - \frac{\pi}{3} \) lies in the third quadrant. In the third quadrant, tan is positive. We change tan to its complementary i.e. cot.
Therefore, \( \tan\left(\frac{7\pi}{2} - \frac{\pi}{3}\right) = +\cot \frac{\pi}{3} = +\frac{1}{\sqrt{3}} \)
Example
Find the value of \( \sec\left(\frac{15\pi}{2} + \frac{\pi}{3}\right) \).
Solution:
\( \frac{15\pi}{2} \) is a vertical angle and its terminal point lies on positive \( y \)-axis.
Thus, \( \frac{15\pi}{2} + \frac{\pi}{3} \) lies in the second quadrant where secant is negative.
Therefore, \( \sec\left(\frac{15\pi}{2} + \frac{\pi}{3}\right) = -\csc \frac{\pi}{3} = -\frac{2}{\sqrt{3}} \)
Visualization of Trigonometric Functions
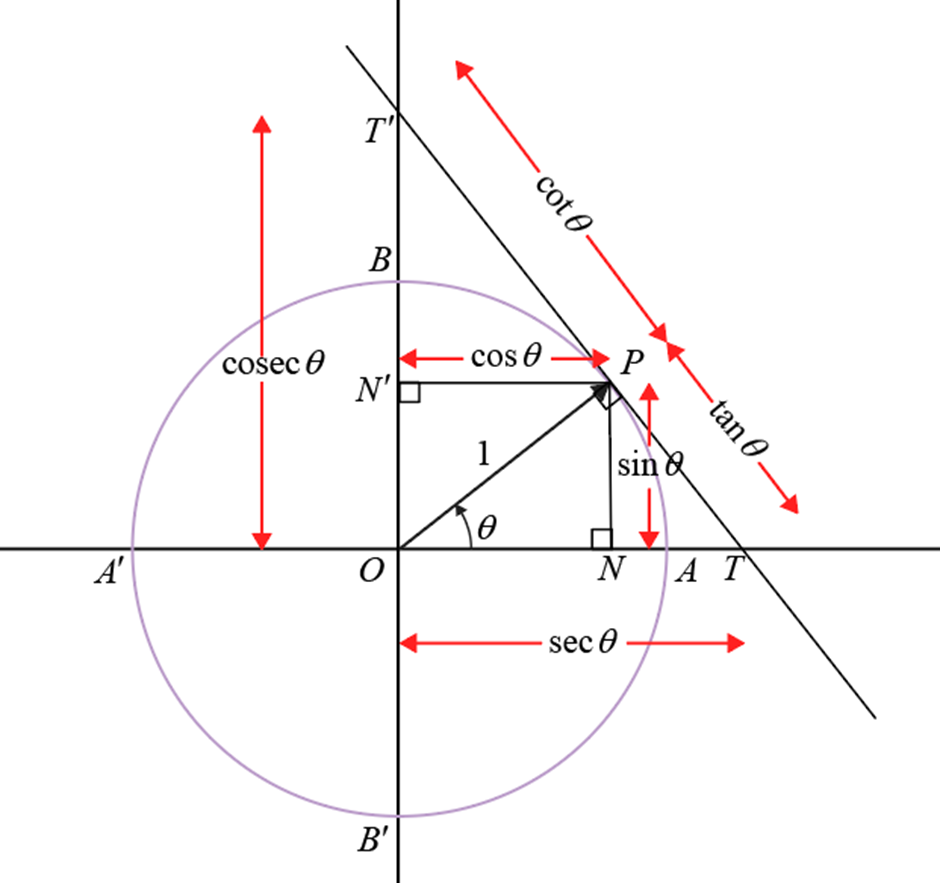
We may visualize trigonometric functions on a single figure as lengths of line segments. Have you ever wondered why the name “tangent” of one of the trigonometric functions? Are there other trigonometric functions?
Let there be a unit circle intersecting axes at \( A, B, A' \) and \( B' \). There is a point \( P \) in the first quadrant on the circle. From point \( P \), draw normals to x-axis and y-axis such that they intersect at \( N \) and \( N' \) respectively. Also draw a tangent to the circle at point \( P \) such that it intersects the x-axis and y-axis at \( T \) and \( T' \) respectively.
In \( \triangle OPN \) which is a right-angled triangle, let angle \( NOP \) be \( \theta \). Clearly, \( P \) is the terminal point of angle \( \theta \).
In \( \triangle OPN \) \( \sin \theta = \frac{PN}{OP} = \frac{PN}{1} = PN \), \( \cos \theta = \frac{ON}{OP} = \frac{ON}{1} = ON \)
Thus, \( PN = \sin \theta \) and \( PN' = ON = \cos \theta \)
“Sine” means “half of the chord”. \( PN \) is equal to the half of the length of the chord \( PP' \), where \( P' \) is the point on the circle when \( PN \) is extended.
“Cosine” is the sine of the complementary angle of \( \theta \). Can you see why?
\( \triangle OPN \) is similar to \( \triangle OPT \) (why?)
\( \Rightarrow \frac{PN}{PT} = \frac{ON}{OP} \) (Corresponding sides are proportional)
\( \Rightarrow PT = \frac{PN}{ON} \)
But according to right trigonometry \( \frac{PN}{ON} = \tan \theta \)
Thus, \( PT = \tan \theta \)
Similarly, you can prove other results shown in the figure.
Plotting trigonometric functions
By plotting the graph one can find and understand more properties of trigonometric functions. They will prove to be of immense importance at many places while solving problems.
What we want to analyse is, for example, how value of sin \( \theta \) changes when \( \theta \) changes. Let us see how.
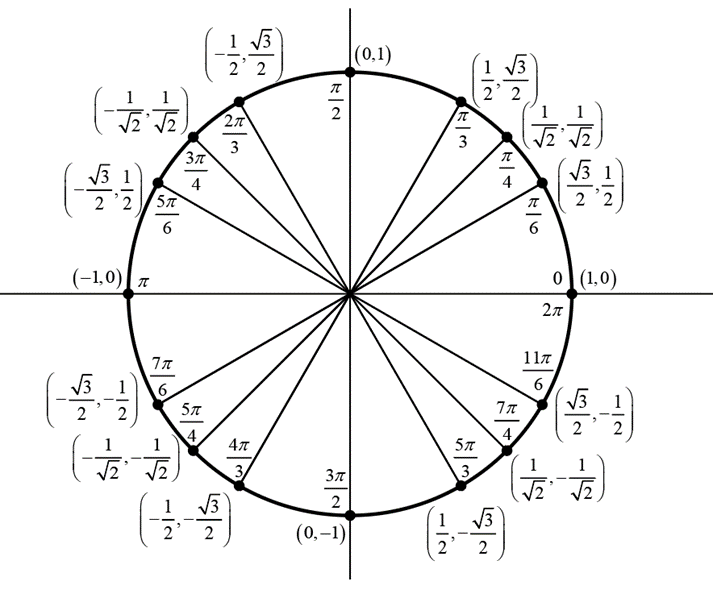
We will use the unit circle below:
It just shows coordinates of terminal points for some of the angles from 0 to \( 2\pi \). It will help us plot graphs easily.
We can easily observe a few important things about the graphs even before drawing them:
-
Trigonometric functions must be periodic because when we move around the circle values repeat themselves.
-
Values of sine and cosine lie in the interval \([-1,1]\) because sine and cosine an angle are ordinate and abscissa of its terminal point. And clearly on a unit circle ordinate abscissa lie in the interval \([-1,1]\).
-
Sine and cosine are defined for angles, thus, their domain, we say, is \( \mathbb{R} \). But that is not so with other trigonometric functions and we can easily conclude why.
Since \( \tan \theta = \frac{y}{x} \), it must be not defined for angles for which \( x \), that is, the abscissa of terminal point is zero. On the unit circle you can see that it is so for all vertical angles i.e. \( \theta = (2n+1)\frac{\pi}{2} \), \( n \in \mathbb{Z} \). Thus, the domain of \( \tan \theta \) is \( \mathbb{R} - \{ \theta : \theta = (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} \} \).
Similarly, \( \sec \theta = \frac{1}{x} \) is also not defined for vertical angles \( \theta = (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} \)
On the other hand, \( \cot \theta = \frac{x}{y} \) \( \Rightarrow \cot \theta \) is not defined for all angles for which \( y \), that is, ordinate is equal to zero. This is so for all horizontal angles, as can be seen on the unit circle. Thus, the domain of \( \cot \theta \) is \( \mathbb{R} - \{ \theta : \theta = n\pi, n \in \mathbb{Z} \} \)
Similarly, the domain of \( \csc \theta \) is also \( \mathbb{R} - \{ \theta : \theta = n\pi, n \in \mathbb{Z} \} \)
| Trigonometric Function | Domain | Range |
|---|---|---|
| sine | \( \mathbb{R} \) | \([-1,1]\) |
| cosine | \( \mathbb{R} \) | \([-1,1]\) |
| tangent | \( \mathbb{R} - \{ \theta : \theta = (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
| cotangent | \( \mathbb{R} - \{ \theta : \theta = n\pi, n \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
| secant | \( \mathbb{R} - \{ \theta : \theta = (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1,1) \) |
| cosecant | \( \mathbb{R} - \{ \theta : \theta = n\pi, n \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1,1) \) |