Inclination and Slope of a Line

Inclination of Lines

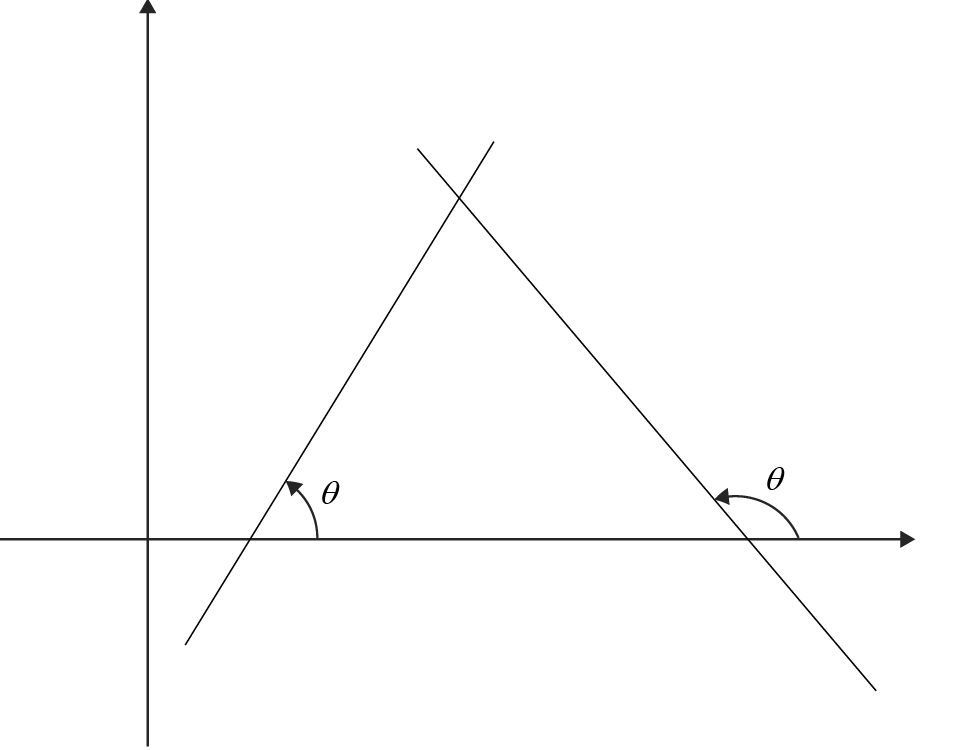
The inclination of a straight line is defined as the angle \(\theta\) that the line forms with the positive x-axis, measured in the counterclockwise direction. The angle \(\theta\) is confined within the range \(0 \leq \theta < \pi\). For a horizontal line, the inclination is \(0\) as it lies along the x-axis. For a vertical line, the inclination is \(\frac{\pi}{2}\), indicating a \(90^\circ\) angle from the x-axis, aligning with the positive y-axis.

Slope of a Line

The slope of a line in the Cartesian coordinate system is defined as the tangent of the inclination of the line. The inclination, \(\theta\), is the angle measured counterclockwise from the positive x-axis to the line. Thus, the slope \(m\) of the line is given by \(m = \tan(\theta)\).

The slope \(m\) of a line, defined as \(m = \tan(\theta)\) where \(\theta\) is the inclination of the line with the positive x-axis, varies depending on the value of \(\theta\):

1. \(\theta = 0\): When the angle of inclination is \(0\), the line is horizontal. Here, \(\tan(0) = 0\), so the slope of the line is \(0\).

2. \(\theta = \frac{\pi}{2}\): At \(\theta = \frac{\pi}{2}\) radians, the line is vertical. The tangent function is undefined at \(\frac{\pi}{2}\), corresponding to an undefined slope for the vertical line.

3. \(\theta\) is acute (\(0 < \theta < \frac{\pi}{2}\)): For acute angles, \(\tan(\theta)\) yields a positive value, indicating a positive slope. This reflects a line rising from left to right.

4. \(\theta\) is obtuse (\(\frac{\pi}{2} < \theta < \pi\)): For obtuse angles, \(\tan(\theta)\) yields a negative value, indicating a negative slope. This reflects a line falling from left to right.

Variation of Slope with Line Rotation in the Cartesian Coordinate System

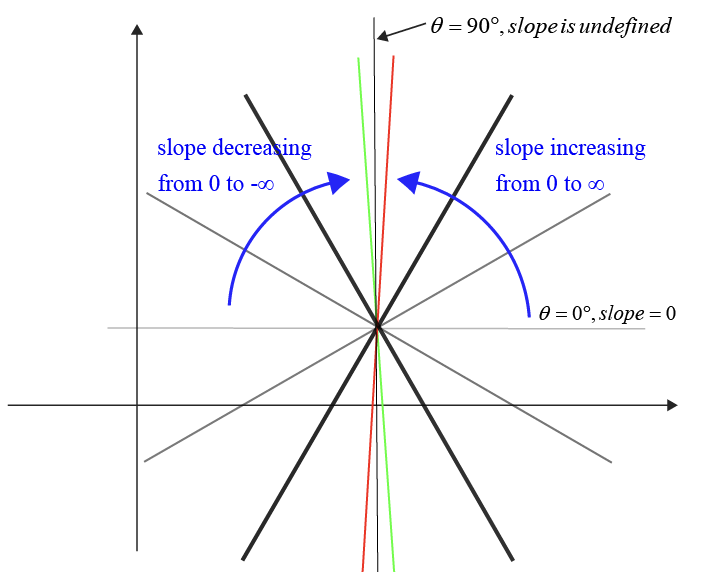
As a line rotates in the Cartesian coordinate system from an inclination \(\theta = 0\) to \(\theta = \frac{\pi}{2}\), the value of the slope \(m = \tan(\theta)\) undergoes a continuous transformation:

1. From \(\theta = 0\) to \(\theta = \frac{\pi}{2}\):

   • At \(\theta = 0\), the line is horizontal, and the slope \(m\) is \(0\).
   • As \(\theta\) increases from \(0\) to \(\frac{\pi}{2}\), the line becomes steeper. The value of \(\tan(\theta)\) increases from \(0\) to positive infinity. Thus, the slope \(m\) increases continuously and becomes infinitely large as the line approaches vertical orientation at \(\theta = \frac{\pi}{2}\), where \(\tan(\theta)\) is undefined due to verticality.

2. From \(\theta = \pi\) to \(\theta = \frac{\pi}{2}\):

   • At \(\theta = \pi\), the line is again horizontal, pointing in the negative direction of the x-axis, and the slope \(m\) is \(0\).
   • Decreasing \(\theta\) from \(\pi\) back to \(\frac{\pi}{2}\) involves the line transitioning from a horizontal to a vertical orientation. As \(\theta\) decreases to slightly less than \(\pi\), the slope \(m\) remains \(0\) since it is still horizontal.
   • As \(\theta\) further decreases towards \(\frac{\pi}{2}\), the line tilts downwards, making the slope negative. The value of \(\tan(\theta)\) decreases from \(0\) to negative infinity as the line becomes a negative slope, getting infinitely steep as it approaches verticality at \(\theta = \frac{\pi}{2}\) from the left. Here, the slope again approaches negative infinity.

In both scenarios, as the line approaches vertical orientation (\(\theta = \frac{\pi}{2}\)), the slope approaches infinity in magnitude but differs in sign based on the direction of approach—positive as \(\theta\) approaches \(\frac{\pi}{2}\) from \(0\) and negative as \(\theta\) approaches \(\frac{\pi}{2}\) from \(\pi\).

Slope of a line using coordinates of two points on the line

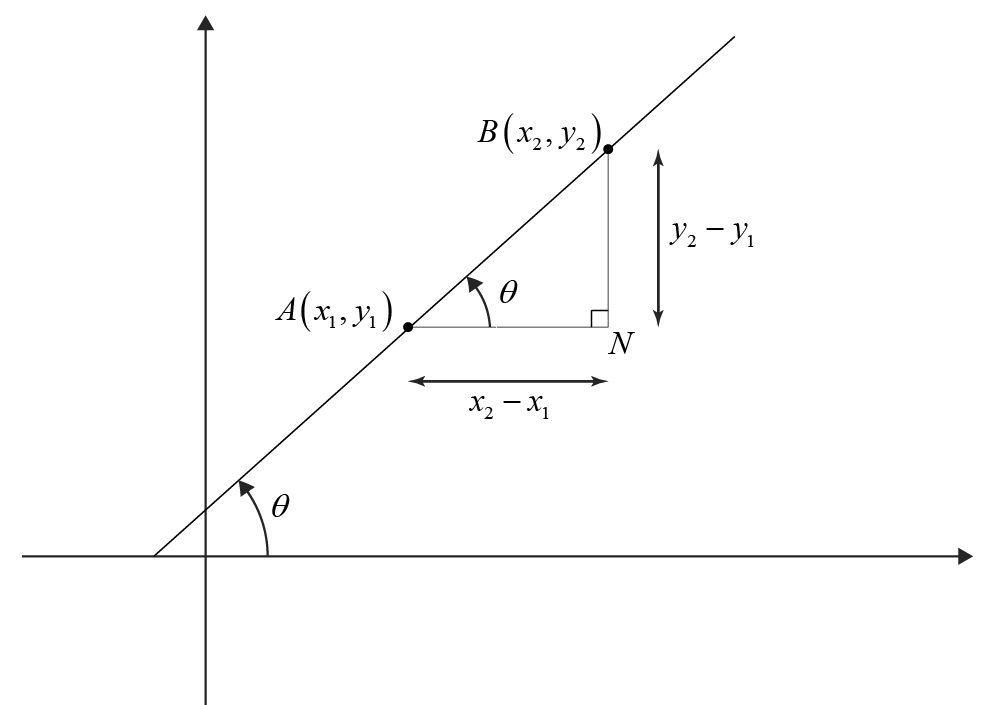
Consider a line in the Cartesian coordinate system. Let \( A \) and \( B \) be two points with known coordinates \( A(x_1, y_1) \) and \( B(x_2, y_2) \), respectively. The slope of the line, which quantifies its steepness, is the tangent of the angle of inclination \( \theta \) that the line makes with the positive direction of the x-axis.

By constructing a right triangle \( ABN \) with the hypotenuse \( AB \) and \( BN \) perpendicular to the x-axis, the angle \( \theta \) is formed at \( N \). The vertical leg \( BN \) represents the change in y-coordinates, \( y_2 - y_1 \), while the horizontal leg \( AN \) represents the change in x-coordinates, \( x_2 - x_1 \).

The slope \( m \) of the line is defined as the ratio of the opposite to the adjacent side of the angle of inclination in triangle \( ABN \), given by the relation \( m = \tan(\theta) = \frac{BN}{AN} \). Simplifying, we obtain the slope of the line as \( m = \frac{y_2 - y_1}{x_2 - x_1} \), providing a measure of the line's steepness in the coordinate plane.

Example

Given two points \( A(1, 2) \) and \( B(4, 6) \), the slope \( m \) of the line through these points is computed using the formula:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

Substituting the coordinates into the formula yields:

\[ m = \frac{6 - 2}{4 - 1} = \frac{4}{3} \]

Thus, the slope of the line through points \( A(1, 2) \) and \( B(4, 6) \) is \( \frac{4}{3} \).

Acute Angle between lines

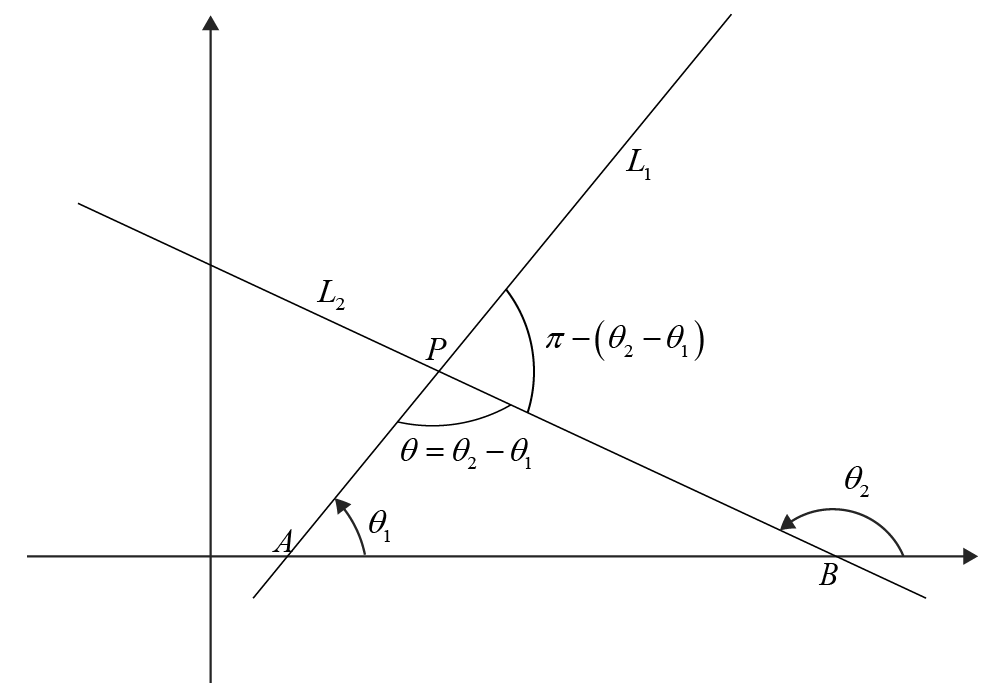
Consider two lines \( L_1 \) and \( L_2 \) intersecting at point \( P \) in the Cartesian plane. Line \( L_1 \) forms an angle \( \theta_1 \) with the positive x-axis, while line \( L_2 \) forms an angle \( \theta_2 \). The angle between the two lines, denoted as \( \theta \), is the difference between \( \theta_2 \) and \( \theta_1 \), that is, \( \theta = \theta_2 - \theta_1 \).

To find the acute angle \( \theta \) between \( L_1 \) and \( L_2 \), consider the exterior angle \( \theta_2 \) at point \( B \) in triangle \( PAB \). The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Hence, \( \theta_2 = \theta + \theta_1 \).

Taking the tangent of both sides to find the slope in terms of the angle, we have:

\[ \tan(\theta) = \tan(\theta_2 - \theta_1) \]

By the identity for the tangent of the difference of two angles, we have:

\[ \tan(\theta) = \frac{\tan(\theta_2) - \tan(\theta_1)}{1 + \tan(\theta_1)\tan(\theta_2)} \]

Given that \( \tan(\theta_1) = m_1 \) and \( \tan(\theta_2) = m_2 \), where \( m_1 \) and \( m_2 \) are the slopes of lines \( L_1 \) and \( L_2 \) respectively, the equation becomes:

\[ \tan(\theta) = \frac{m_2 - m_1}{1 + m_1m_2} \]

The other angle formed by the intersection of \( L_1 \) and \( L_2 \) is \( \pi - (\theta_2 - \theta_1) \), and its tangent will be the negative of \( \tan(\theta) \). One of the angle is acute anf the other is obtuse. Since we know that tangent of acute angle is always positive, \(\left|\frac{m_2 - m_1}{1 + m_1m_2}\right|\) gives the tangent of acute angle between the lines.

Thus, the tangent of the acute angle between the lines is given by

\[ \tan(\theta) = \left|\frac{m_2 - m_1}{1 + m_1m_2}\right| \]

Example

Given a quadrilateral \( ABCD \) with vertices at \( A(4,3) \), \( B(-3,5) \), \( C(-1, -1) \), and \( D(2,-5) \), the task is to find the tangent of the acute angle between the diagonals \( AC \) and \( BD \).

Solution:

First, compute the slopes of the diagonals \( AC \) and \( BD \).

The slope \( m_{AC} \) of diagonal \( AC \) is determined by the coordinates of points \( A \) and \( C \):

\[ m_{AC} = \frac{y_C - y_A}{x_C - x_A} = \frac{-1 - 3}{-1 - 4} = \frac{-4}{-5} = \frac{4}{5} \]

Similarly, the slope \( m_{BD} \) of diagonal \( BD \) is found using the coordinates of points \( B \) and \( D \):

\[ m_{BD} = \frac{y_D - y_B}{x_D - x_B} = \frac{-5 - 5}{2 - (-3)} = \frac{-10}{5} = -2 \]

The angle \( \theta \) between the two diagonals can then be calculated using the tangent of the difference between their angles of inclination, \( \theta_1 \) and \( \theta_2 \), where \( \tan(\theta_1) = m_{AC} \) and \( \tan(\theta_2) = m_{BD} \). The formula for the tangent of the angle between two lines is:

\[ \tan(\theta) = \left| \frac{m_{BD} - m_{AC}}{1 + m_{AC}m_{BD}} \right| \]

Substitute the values of \( m_{AC} \) and \( m_{BD} \) into the formula:

\[ \tan(\theta) = \left| \frac{-2 - \frac{4}{5}}{1 + \frac{4}{5}(-2)} \right| \]

\[ \tan(\theta) = \left| \frac{-10 - 4}{5 + 5(-2)} \right| \]

\[ \tan(\theta) = \left| \frac{-14}{5 - 10} \right| \]

\[ \tan(\theta) = \left| \frac{-14}{-5} \right| \]

\[ \tan(\theta) = \frac{14}{5} \]

Hence, the tangent of the acute angle between diagonals \( AC \) and \( BD \) of quadrilateral \( ABCD \) is \( \frac{14}{5} \).

Measuring a particular angle between lines

Consider a triangle formed by three distinct points \( A \), \( B \), and \( C \) in a Cartesian coordinate system. The objective is to measure all interior angles of the triangle precisely. Typically, plotting the points and visually estimating the angles can lead to uncertainty, especially when distinguishing between acute and obtuse angles. This is due to the potential inaccuracy of graphical representation and the subjective nature of visual estimation.

The formula we derived above can only calculate acute angle between two lines. So how do we measure a particular angle between two lines.

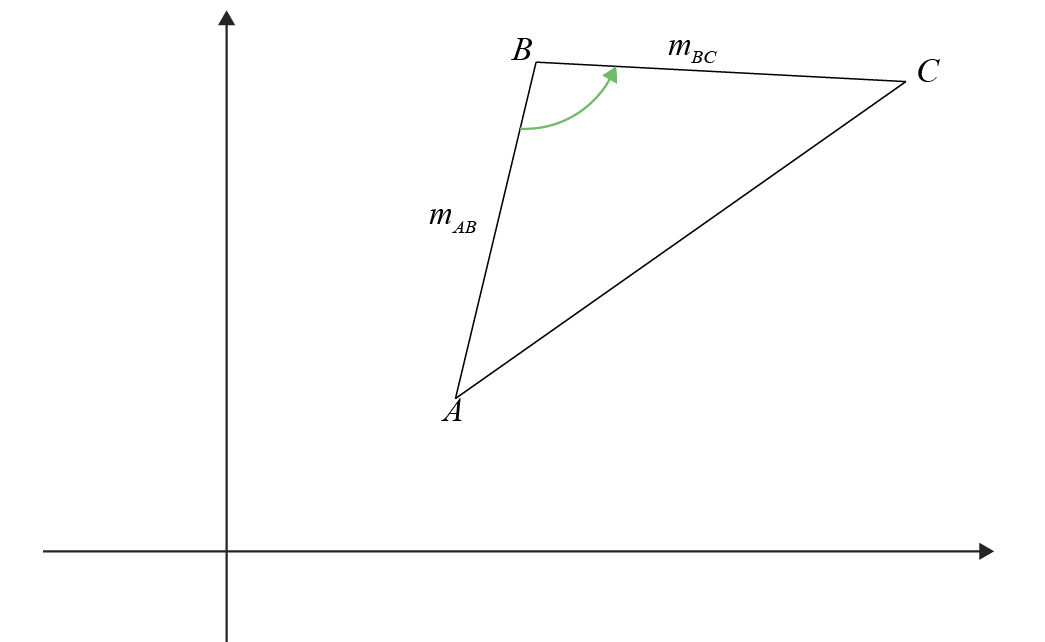
Plot the lines and identify the angle that you want to measure. Draw an anticlockwise arc with an arrow at the head.

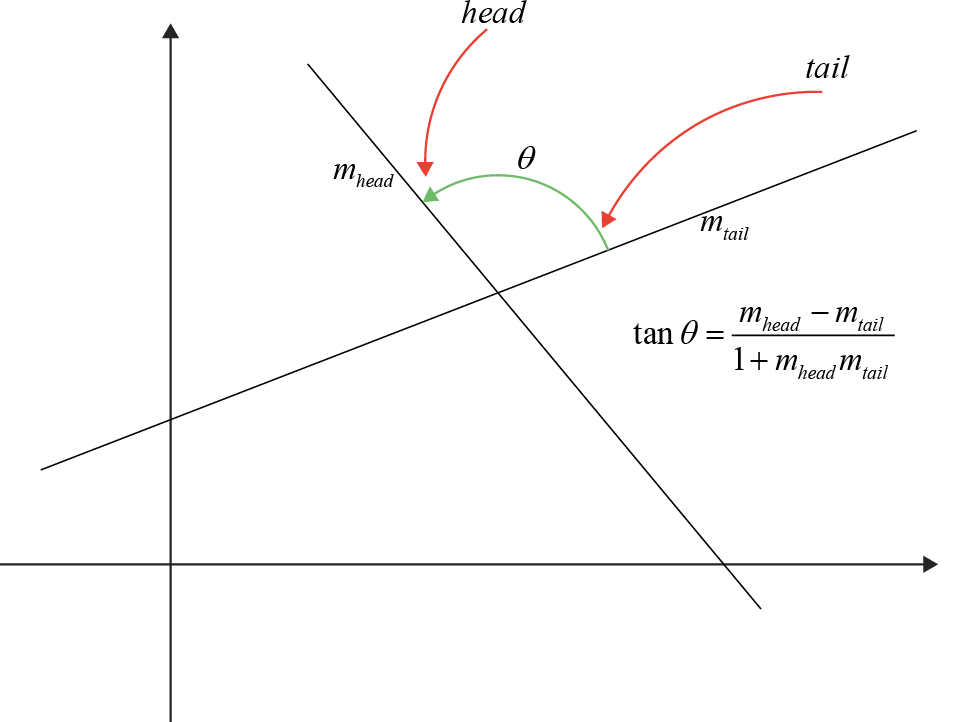
The formula for the tangent of the angle between these two intersecting lines, where \( m_{tail} \) is the slope of the line at the initial side (tail) and \( m_{head} \) is the slope of the line at the terminal side (head), is given by:

\[ \tan(\theta) = \frac{m_{head} - m_{tail}}{1 + m_{head}m_{tail}} \]

Tbus, the tangent of the angle \( \angle ABC \) can be calculated using the formula for the tangent of the difference of two angles, considering the orientation of the angle measured anticlockwise from line \( AB \) to line \( BC \).

\[ \tan(\angle ABC) = \frac{m_{BC} - m_{AB}}{1 + m_{AB}m_{BC}} \]

This formula yields the tangent of the angle \( \angle ABC \), regardless of whether it is acute or obtuse. The slopes \( m_{AB} \) and \( m_{BC} \) can be determined from the coordinates of the points \( A \), \( B \), and \( C \), after which the formula can be used to find the tangent of the measured angle.

Example

Determine the tangents of the interior angles \( \angle A \), \( \angle B \), and \( \angle C \) for triangle \( ABC \) with vertices at \( A(3,3) \), \( B(-2,4) \), and \( C(0,-5) \).

Solution:

Calculate the slopes of the sides \( AB \), \( BC \), and \( CA \):

Slope of \( AB \) (\( m_{AB} \)):

\[ m_{AB} = \frac{y_B - y_A}{x_B - x_A} = \frac{4 - 3}{-2 - 3} = \frac{1}{-5} = -\frac{1}{5} \]

Slope of \( BC \) (\( m_{BC} \)):

\[ m_{BC} = \frac{y_C - y_B}{x_C - x_B} = \frac{-5 - 4}{0 - (-2)} = \frac{-9}{2} \]

Slope of \( CA \) (\( m_{CA} \)):

\[ m_{CA} = \frac{y_A - y_C}{x_A - x_C} = \frac{3 - (-5)}{3 - 0} = \frac{8}{3} \]

Draw anticlockwise arrows at each angle. Apply the tangent formula to find the tangent of each angle, where \( \tan(\theta) = \frac{m_{\text{head}} - m_{\text{tail}}}{1 + m_{\text{head}} \cdot m_{\text{tail}}} \):

For \( \angle A \), which is between \( CA \) and \( AB \):

\[ \tan(A) = \frac{m_{CA} - m_{AB}}{1 + m_{CA} \cdot m_{AB}} = \frac{\frac{8}{3} - \left(-\frac{1}{5}\right)}{1 + \frac{8}{3} \cdot \left(-\frac{1}{5}\right)} \]

\[ \tan(A) = \frac{\frac{40}{15} + \frac{3}{15}}{1 - \frac{8}{15}} = \frac{\frac{43}{15}}{\frac{7}{15}} = \frac{43}{7} \]

For \( \angle B \), between \( AB \) and \( BC \):

\[ \tan(B) = \frac{m_{AB} - m_{BC}}{1 + m_{AB} \cdot m_{BC}} = \frac{-\frac{1}{5} - \left(-\frac{9}{2}\right)}{1 + \left(-\frac{1}{5}\right) \cdot \left(-\frac{9}{2}\right)} \]

\[ \tan(B) = \frac{-\frac{1}{5} + \frac{9}{2}}{1 + \frac{9}{10}} = \frac{-\frac{2}{10} + \frac{45}{10}}{1 + \frac{9}{10}} = \frac{\frac{43}{10}}{\frac{19}{10}} = \frac{43}{19} \]

For \( \angle C \), which is between \( BC \) and \( CA \):

\[ \tan(C) = \frac{m_{BC} - m_{CA}}{1 + m_{BC} \cdot m_{CA}} = \frac{-\frac{9}{2} - \frac{8}{3}}{1 + \left(-\frac{9}{2}\right) \cdot \frac{8}{3}} \]

\[ \tan(C) = \frac{-\frac{27}{6} - \frac{16}{6}}{1 - \frac{72}{6}} = \frac{-\frac{43}{6}}{1 - 12} = \frac{-\frac{43}{6}}{-11} = \frac{43}{66} = \frac{43}{66} \]

Since the tangent of an acute angle is positive and the tangent of an obtuse angle is negative (when considering angles in standard position), the signs will indicate the nature of each angle.

From the previous calculations, we have:

• \( \tan(A) = \frac{43}{7} \), which is positive, indicating that \( \angle A \) is acute.
• \( \tan(B) = \frac{43}{19} \), which is also positive, so \( \angle B \) is acute.
• \( \tan(C) = \frac{43}{66} \), again positive, suggesting that \( \angle C \) is acute.

Since all angles have positive tangents and are therefore acute, triangle \( ABC \) is an acute triangle.

Parallel and Perpendicular Lines

For two lines with slopes \( m_1 \) and \( m_2 \), the relationship between the slopes and the angle \( \theta \) between the lines can be expressed using the tangent function:

\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]

1. Parallel Lines: If two lines are parallel, the angle \( \theta \) between them is \( 0 \) degrees (or \( 0 \) radians). In this case, \( \tan(\theta) = \tan(0) = 0 \), which leads to the equation:

   \[ 0 = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]

   Since the absolute value is zero only when the quantity inside is zero, it implies that \( m_2 - m_1 = 0 \), or \( m_1 = m_2 \).

2. Perpendicular Lines: For two lines to be perpendicular, \( \theta \) is \( 90 \) degrees (or \( \frac{\pi}{2} \) radians), and thus \( \tan(\theta) \) should be undefined. This is only the case when the denominator of the tangent function is zero:

   \[ 1 + m_1m_2 = 0 \]

   Solving for \( m_2 \) gives us \( m_2 = -\frac{1}{m_1} \), indicating that the slopes of perpendicular lines are negative reciprocals of each other.