Evaluating and Visualizing a quadratic expression
Evaluating a Quadratic Expression: The Transformer Concept
Evaluating a quadratic expression can be conceptualized as a process where the expression acts as a "transformer" that converts one real number into another.
-
Input (The Real Number): The process begins with an input, say \( x \), which is a real number. This number is what we feed into our quadratic expression.
-
The Quadratic Expression (The Transformer): The expression \( ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are constants, then acts on this input. The transformation involves:
- Squaring the input (\( x^2 \)),
- Multiplying it by the coefficient \( a \),
- Adding the product of the input and the coefficient \( b \),
- Finally, adding the constant \( c \).
-
Output (Transformed Real Number): The result of this process is another real number, which is the output of the quadratic expression for the given input. This output can be vastly different from the input, depending on the values of \( a \), \( b \), and \( c \).
Example
Consider a simple quadratic expression: \( 2x^2 - 3x + 1 \).
- If we input \( x = 2 \) into this expression, the transformation process looks like this:
So, the output for this input is \( 3 \).
Visualizing the Transformation
In a broader sense, this transformation can be visualized on a graph, where each input corresponds to a point on the curve of the quadratic function. The nature of this curve (a parabola) reflects how the expression transforms different inputs, illustrating the variation in outputs for different values of \( x \).
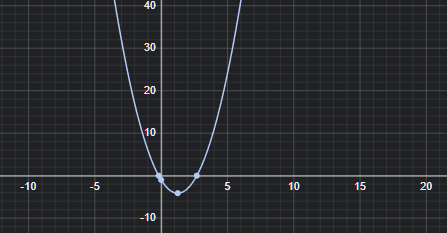
For instance, to draw the graph of the quadratic expression \( 2x^2 - 5x - 1 \) with inputs ranging from -5 to 5 with a step size of 0.5, you can follow these steps and tabulate the results:
-
Define the Quadratic Expression: The expression is given by \( y = 2x^2 - 5x - 1 \).
-
Calculate Values: For each x-value from -5 to 5 in steps of 0.5, calculate the corresponding y-value using the expression.
-
Create a Table: Tabulate the x-values and their corresponding y-values.
Here is an example table showing a few selected values:
x y -5.0 \( 2(-5)^2 - 5(-5) - 1 \) -4.5 \( 2(-4.5)^2 - 5(-4.5) - 1 \) ... ... 4.5 \( 2(4.5)^2 - 5(4.5) - 1 \) 5.0 \( 2(5)^2 - 5(5) - 1 \) -
Plot the Graph: Use the values from the table to plot the graph, marking the points and drawing a curve through them.
Your graph should eventually look like this.
Learning from the Graph of a Quadratic Expression
When you start learning about quadratic expressions, looking at their graphs can be really helpful. A quadratic expression is usually in the form \( ax^2 + bx + c \), and its graph is a curve called a parabola. Here's what you can learn from this graph:
-
Range:
- The range is all the possible values that \( y \) (the output) can take.
- If the parabola opens upwards (like a smile), the range includes all values above the lowest point of the parabola.
- If it opens downwards (like a frown), the range includes all values below the highest point of the parabola.
-
Maximum and Minimum Values:
- The highest or lowest point of the parabola is really important.
- If the parabola opens upwards, this lowest point gives you the minimum value of \( y \).
- If it opens downwards, the highest point gives you the maximum value of \( y \).
-
When does the Graph Increase or Decrease?:
- Look at the parabola: before reaching its lowest or highest point, the values of \( y \) either go down (decrease) or go up (increase).
- After that point, they change direction. So, this point (called the vertex) is where the graph switches from increasing to decreasing, or vice versa.
-
Axis of Symmetry:
- The parabola is symmetrical. There's a line that splits it into two equal halves, called the axis of symmetry.
-
Roots or X-Intercepts:
- These are where the graph touches or crosses the x-axis. They tell you the values of \( x \) when \( y = 0 \).
-
Y-Intercept:
- It's the point where the graph crosses the y-axis and shows you the value of the quadratic expression when \( x = 0 \).
-
Shape of the Parabola:
- The number in front of \( x^2 \) (that's \( a \) in \( ax^2 + bx + c \)) affects how wide or narrow the parabola is.
By looking at the graph, you can get a good feel for how the quadratic expression behaves, which helps a lot in understanding these math concepts better!
Not the best way
Clearly drawing graphs by manually putting a lot of points can be tediuos for comlex expressions. For a quadratic expression, at least, we have a better way. You are going to learn about it in the upcoming sections.