Relation of Roots with Graphs

The roots of a quadratic expression and their relation to the graph can be understood by exploring six different scenarios based on the coefficient \( a \) and the discriminant \( \Delta \) of the quadratic expression \( ax^2 + bx + c \). Here, \( \Delta = b^2 - 4ac \) helps determine the nature of the roots.

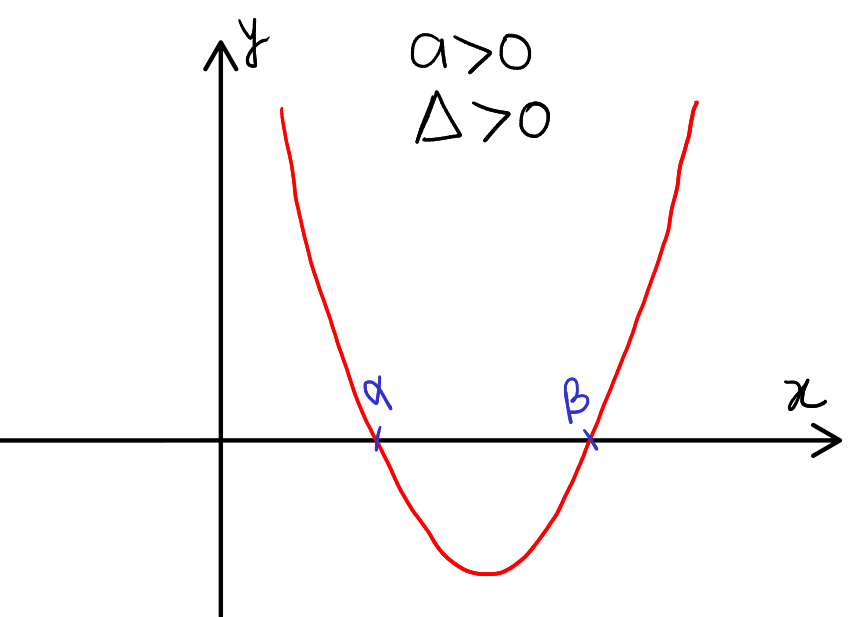
Case 1: \( a > 0 \) and \( \Delta > 0 \)

• Graph Behavior: The parabola opens upwards.
• Roots: Two distinct real roots, \( \alpha \) and \( \beta \), with \( \alpha < \beta \).
• Interpretation: The quadratic function intersects the x-axis at points \( \alpha \) and \( \beta \). For all \( x < \alpha \) and \( x > \beta \), the expression \( ax^2 + bx + c > 0 \), indicating the graph lies above the x-axis. However, for \( \alpha < x < \beta \), the expression \( ax^2 + bx + c < 0 \), and the graph dips below the x-axis.

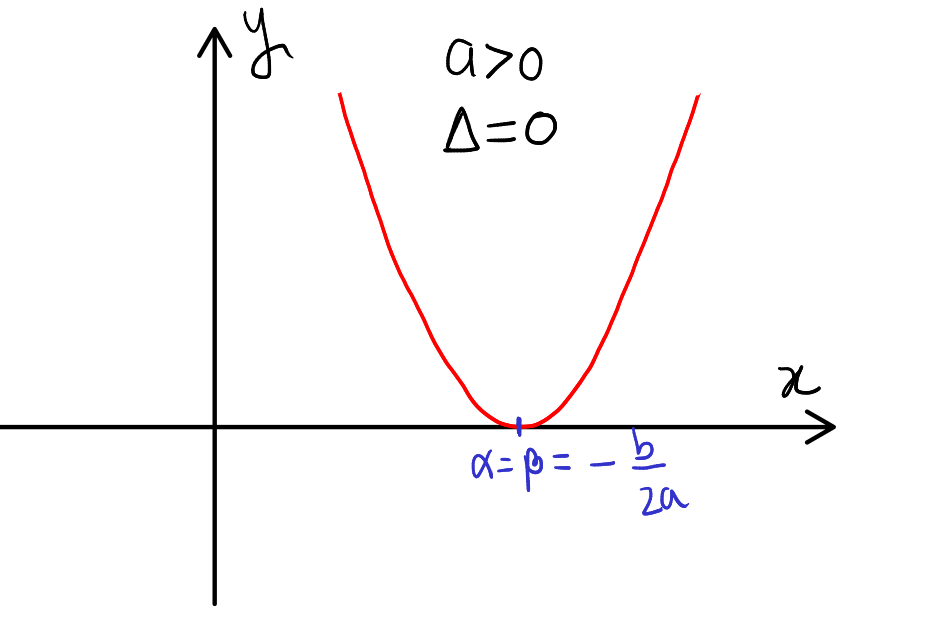
Case 2: \( a > 0 \) and \( \Delta = 0 \)

• Graph Behavior: The parabola opens upwards.
• Roots: One real, repeated root, say \( \alpha \).
• Interpretation: The quadratic function touches the x-axis exactly at \( \alpha \) (the vertex of the parabola). For all \( x \in \mathbb{R} \), \( ax^2 + bx + c \geq 0 \), indicating the graph is always on or above the x-axis. The function is non-negative across its domain.

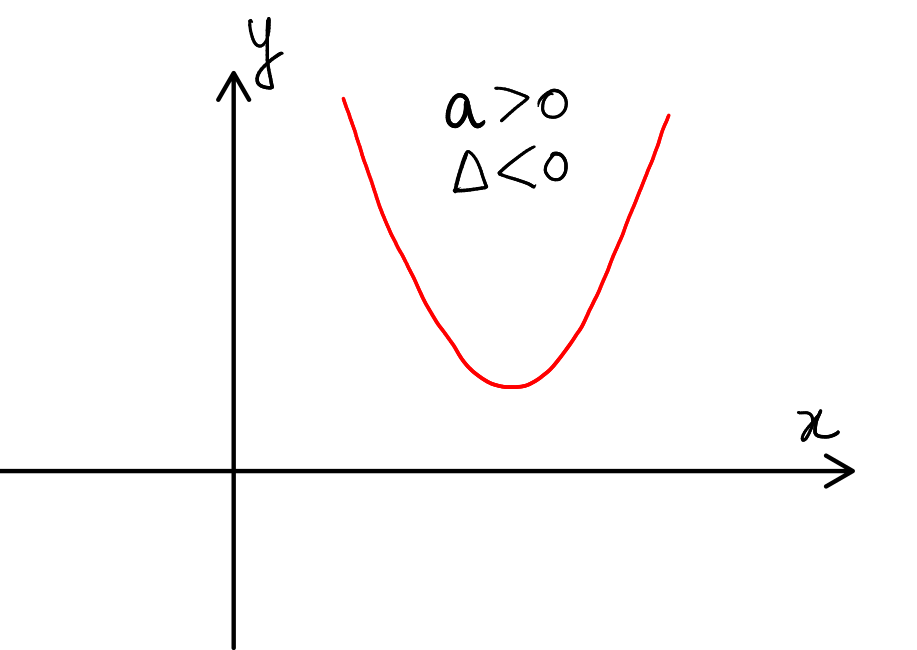
Case 3: \( a > 0 \) and \( \Delta < 0 \)

• Graph Behavior: The parabola opens upwards.
• Roots: No real roots.
• Interpretation: Since \( \Delta < 0 \), there are no x-intercepts, and the graph does not intersect the x-axis. For all \( x \in \mathbb{R} \), \( ax^2 + bx + c > 0 \). The function is strictly positive for all real \( x \).

The sign of c

As we can observe that in case 3, the parabola is positioned entirely above the x-axis, the y-intercept of the parabola at \( y = c \) (the value of the quadratic expression when \( x = 0 \)) is also always above the x-axis, i.e., \(c>0\). You should remember this fact that \( c > 0 \) when \( a > 0 \) and \( \Delta < 0 \).

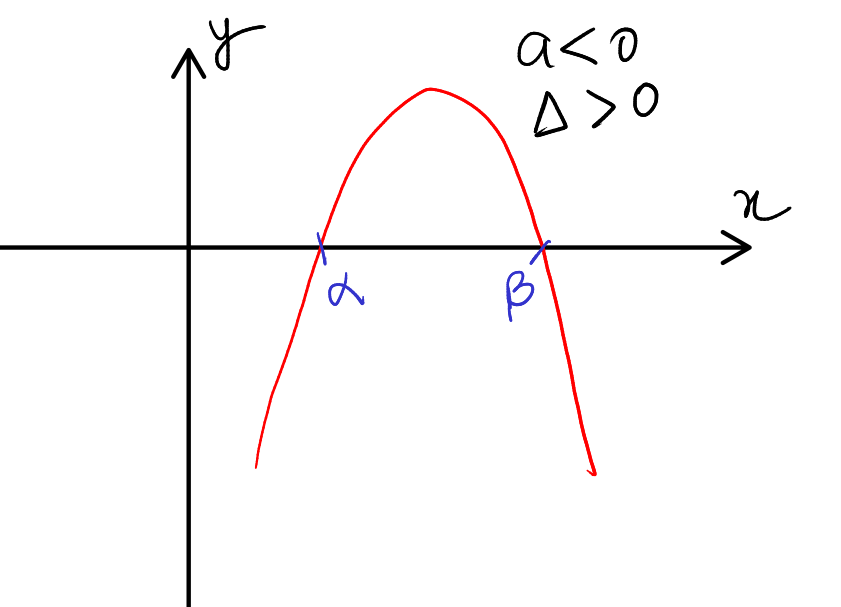
Case 4: \( a < 0 \) and \( \Delta > 0 \)

• Graph Behavior: The parabola opens downwards.
• Roots: Two distinct real roots, \( \alpha \) and \( \beta \), with \( \alpha < \beta \).
• Interpretation: The quadratic function intersects the x-axis at \( \alpha \) and \( \beta \). For \( x < \alpha \) and \( x > \beta \), \( ax^2 + bx + c < 0 \), so the graph is below the x-axis. However, for \( \alpha < x < \beta \), \( ax^2 + bx + c > 0 \), and the graph lies above the x-axis.

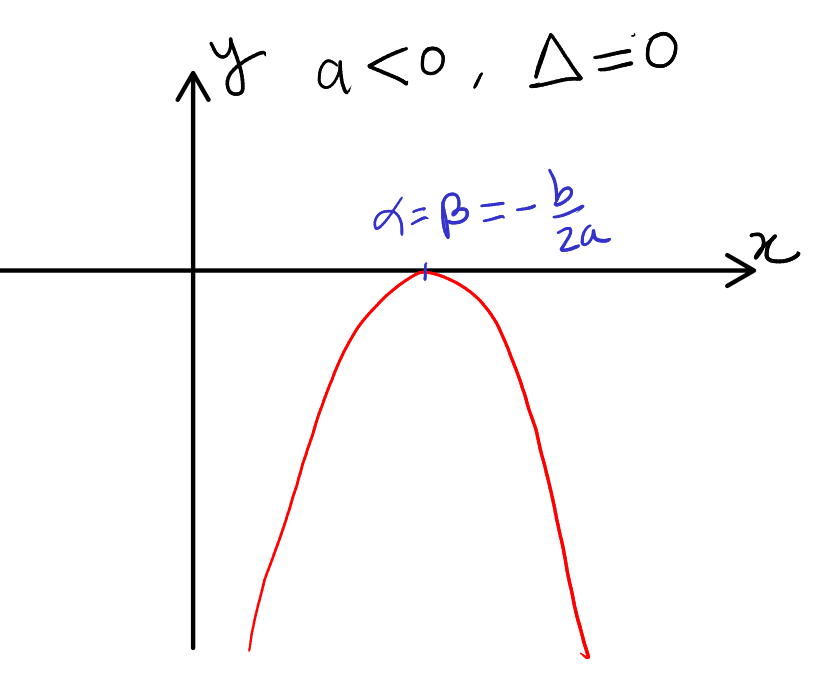
Case 5: \( a < 0 \) and \( \Delta = 0 \)

• Graph Behavior: The parabola opens downwards.
• Roots: One real, repeated root, say \( \alpha \).
• Interpretation: The function touches the x-axis at \( \alpha \). For all \( x \in \mathbb{R} \), \( ax^2 + bx + c \leq 0 \). The graph never goes above the x-axis, and the function is non-positive throughout its domain.

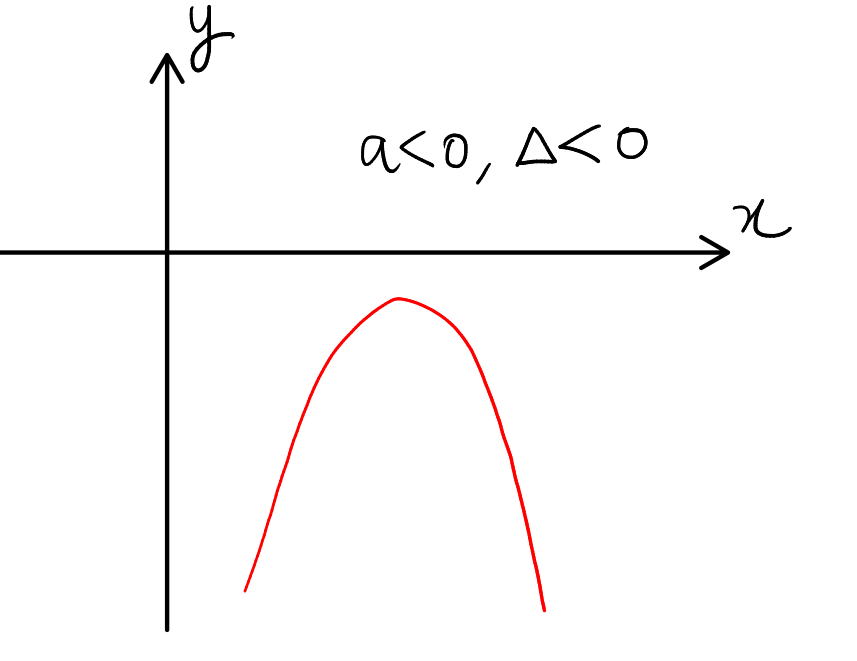
Case 6: \( a < 0 \) and \( \Delta < 0 \)

• Graph Behavior: The parabola opens downwards.
• Roots: No real roots.
• Interpretation: With \( \Delta < 0 \), the quadratic function has no x-intercepts and does not intersect the x-axis. For all \( x \in \mathbb{R} \), \( ax^2 + bx + c < 0 \). The graph is entirely below the x-axis, and the function is strictly negative for all real \( x \).

The sign of c

As we can observe that in case 6, the parabola is positioned entirely below the x-axis, the y-intercept of the parabola at \( y = c \) (the value of the quadratic expression when \( x = 0 \)) is also always below the x-axis, i.e., \(c<0\). Hence, \( c < 0 \) when \( a < 0 \) and \( \Delta < 0 \).

These cases highlight how the discriminant \( \Delta \) and the leading coefficient \( a \) of a quadratic expression determine not only the nature of its roots but also the overall behavior of its graph. Understanding this relationship is crucial in graphing quadratic functions and interpreting their real-world applications.