Angle between pair of Straight Lines

Angle Between a Pair of Straight Lines

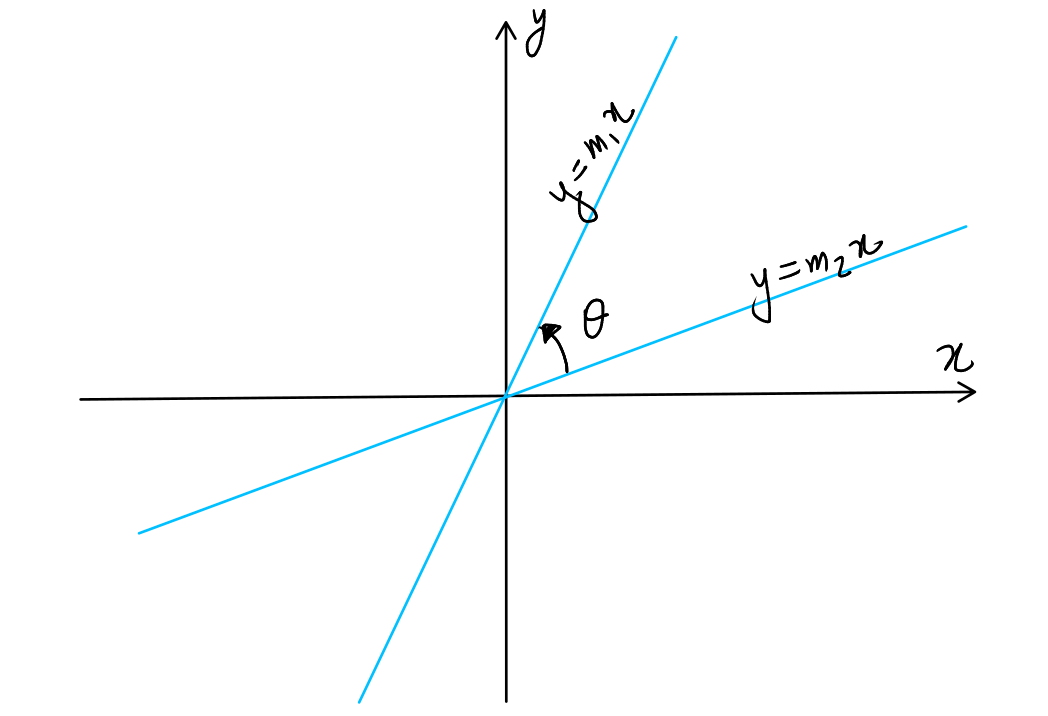
As a first example of the above theory, let us calculate the angle between a pair of straight lines. Consider the joint equation:

\[ ax^2 + 2hxy + by^2 = 0 \]

Let us assume that this equation represents two straight lines \( y = m_1x \) and \( y = m_2x \). Now, we know that:

\[ m_1 + m_2 = -\frac{2h}{b} \]

\[ m_1m_2 = \frac{a}{b} \]

Suppose the acute angle between these lines is \( \theta \). Then:

\[ \tan \theta = \left| \frac{m_1 - m_2}{1 + m_1m_2} \right| \]

Using the identity \( (a - b)^2 = (a+b)^2 - 4ab \), we have:

\[ (m_1 - m_2)^2 = (m_1 + m_2)^2 - 4m_1m_2 \]

Therefore:

\[ \tan^2 \theta = \frac{(m_1 - m_2)^2}{(1 + m_1m_2)^2} = \frac{(m_1 + m_2)^2 - 4m_1m_2}{(1 + m_1m_2)^2} \]

Substituting the values of \( m_1 + m_2 \) and \( m_1m_2 \):

\[ (m_1 + m_2)^2 = \left( -\frac{2h}{b} \right)^2 = \frac{4h^2}{b^2} \]

\[ 4m_1m_2 = 4 \cdot \frac{a}{b} = \frac{4a}{b} \]

Hence:

\[ \tan^2 \theta = \frac{\frac{4h^2}{b^2} - \frac{4a}{b}}{(1 + \frac{a}{b})^2} = \frac{4 \left( \frac{h^2 - ab}{b^2} \right)}{\left( \frac{b + a}{b} \right)^2} = \frac{4(h^2 - ab)}{b^2} \cdot \frac{b^2}{(a + b)^2} = \frac{4(h^2 - ab)}{(a + b)^2} \]

Therefore:

\[ \tan \theta = \sqrt{ \frac{4(h^2 - ab)}{(a + b)^2} } = \frac{2\sqrt{h^2 - ab}}{|a + b|} \]

So, the tangent of the acute angle \( \theta \) between the two straight lines is:

\[ \tan \theta = \frac{2\sqrt{h^2 - ab}}{|a + b|} \]

We can calculate \(\cos \theta\) as follows:

\[ \begin{aligned} \cos \theta &= \frac{|a + b|}{\sqrt{(a + b)^2 + (2\sqrt{h^2 - ab})^2}} \\ &= \frac{|a + b|}{\sqrt{(a + b)^2 + 4(h^2 - ab)}} \\ &= \frac{|a + b|}{\sqrt{a^2 + b^2 + 2ab + 4h^2 - 4ab}} \\ &= \frac{|a + b|}{\sqrt{a^2 + b^2 - 2ab + 4h^2}} \\ &= \frac{|a + b|}{\sqrt{(a - b)^2 + 4h^2}} \end{aligned} \]

Thus:

\[ \cos \theta = \frac{|a + b|}{\sqrt{(a - b)^2 + 4h^2}} \]

Using the identity \(\sin^2 \theta + \cos^2 \theta = 1\), we can find \(\sin \theta\):

\[ \sin \theta = \frac{2\sqrt{h^2 - ab}}{\sqrt{(a - b)^2 + 4h^2}} \]

Hence, we have:

\[ \cos \theta = \frac{|a + b|}{\sqrt{(a - b)^2 + 4h^2}} \]

\[ \sin \theta = \frac{2\sqrt{h^2 - ab}}{\sqrt{(a - b)^2 + 4h^2}} \]

Example

Prove that if the slope of one of the lines represented by \(ax^2 + 2hxy + by^2 = 0\) is twice the other, then \(9ab = 8h^2\).

Proof:

Let the slopes of the lines represented by \(ax^2 + 2hxy + by^2 = 0\) be \(m\) and \(2m\). Then,

From the sum of slopes:

\[ m + 2m = -\frac{2h}{b} \]

\[ 3m = -\frac{2h}{b} \]

\[ m = -\frac{2h}{3b} \]

From the product of slopes:

\[ m \cdot 2m = \frac{a}{b} \]

\[ 2m^2 = \frac{a}{b} \]

Substitute \( m = -\frac{2h}{3b} \) into the product of slopes:

\[ 2 \left(-\frac{2h}{3b}\right)^2 = \frac{a}{b} \]

\[ 2 \cdot \frac{4h^2}{9b^2} = \frac{a}{b} \]

\[ \frac{8h^2}{9b^2} = \frac{a}{b} \]

Multiplying both sides by \(9b^2\):

\[ 8h^2 = 9ab \]

Example

Prove that if the slope of one of the lines represented by \(ax^2 + 2hxy + by^2 = 0\) is \(\lambda\) times the other, then \((\lambda + 1)^2 ab = 4h^2 \lambda\).

Proof:

Let the slopes of the lines represented by \(ax^2 + 2hxy + by^2 = 0\) be \(m\) and \(\lambda m\).

From the sum of slopes:

\[ m + \lambda m = -\frac{2h}{b} \]

\[ (1 + \lambda)m = -\frac{2h}{b} \]

\[ m = \frac{-2h}{b(\lambda + 1)} \]

From the product of slopes:

\[ m \cdot \lambda m = \frac{a}{b} \]

\[ \lambda m^2 = \frac{a}{b} \]

Substitute \( m = \frac{-2h}{b(\lambda + 1)} \) into the product of slopes:

\[ \lambda \left( \frac{-2h}{b(\lambda + 1)} \right)^2 = \frac{a}{b} \]

\[ \lambda \cdot \frac{4h^2}{b^2 (\lambda + 1)^2} = \frac{a}{b} \]

Eliminate \( m \):

\[ \frac{4h^2 \lambda}{b^2 (\lambda + 1)^2} = \frac{a}{b} \]

\[ 4h^2 \lambda = ab (\lambda + 1)^2 \]

Therefore:

\[ (\lambda + 1)^2 ab = 4h^2 \lambda \]

So, we have proved that if the slope of one of the lines represented by \(ax^2 + 2hxy + by^2 = 0\) is \(\lambda\) times the other, then:

\[ (\lambda + 1)^2 ab = 4h^2 \lambda \]

Perpendicular Lines

The lines represented by \( ax^2 + 2hxy + by^2 = 0 \) are perpendicular if and only if \( a + b = 0 \).

Proof:

Let the equation \( ax^2 + 2hxy + by^2 = 0 \) represent two straight lines. These lines can be expressed in the form \( y = m_1x \) and \( y = m_2x \), where \( m_1 \) and \( m_2 \) are the slopes of the lines.

From the given quadratic equation, we know the following relationships:

1. Sum of Slopes: [ m_1 + m_2 = -\frac{2h}{b} ]

2. Product of Slopes: [ m_1m_2 = \frac{a}{b} ]

For the lines to be perpendicular, the product of their slopes must be \(-1\). Thus, we have:

\[ m_1m_2 = -1 \]

Using the given relationship for the product of slopes, we substitute:

\[ \frac{a}{b} = -1 \]

Solving for \( a \) and \( b \):

\[ a = -b \]

Therefore, we can conclude:

\[ a + b = 0 \]

This establishes that for the lines represented by \( ax^2 + 2hxy + by^2 = 0 \) to be perpendicular, the condition \( a + b = 0 \) must be satisfied. Conversely, if \( a + b = 0 \), the product of the slopes \( m_1 \) and \( m_2 \) will be \(-1\), indicating that the lines are indeed perpendicular.

Hence, the theorem is proved.

\[ \boxed{a + b = 0} \]

This completes the proof.

Equation of perpendicular pair of straight lines to a given pair

The equation of a pair of straight lines, each perpendicular to a given pair of straight lines represented by \(ax^2 + 2hxy + by^2 = 0\), is given by \(bx^2 - 2hxy + ay^2 = 0\).

Proof:

Consider the equation of a pair of straight lines passing through the origin:

\[ ax^2 + 2hxy + by^2 = 0. \]

Let this equation represent two lines \(y = m_1x\) and \(y = m_2x\).

We know the following relationships between the slopes \(m_1\) and \(m_2\):

\[ m_1 + m_2 = -\frac{2h}{b} \quad \text{and} \quad m_1 m_2 = \frac{a}{b}. \]

To find the equation of the lines perpendicular to these, we need the slopes of the perpendicular lines. If a line has a slope \(m\), then a line perpendicular to it has a slope \(-\frac{1}{m}\). Therefore, the lines perpendicular to \(y = m_1x\) and \(y = m_2x\) will have equations:

\[ y = -\frac{1}{m_1}x \quad \text{and} \quad y = -\frac{1}{m_2}x. \]

These can be rewritten as:

\[ x + m_1 y = 0 \quad \text{and} \quad x + m_2 y = 0. \]

To find the combined equation representing both these lines, we multiply the individual line equations:

\[ (x + m_1 y)(x + m_2 y) = 0. \]

Expanding this product, we get:

\[ x^2 + (m_1 + m_2)xy + m_1 m_2 y^2 = 0. \]

Substituting the known values of \(m_1 + m_2\) and \(m_1 m_2\) from above, we have:

\[ x^2 + \left(-\frac{2h}{b}\right)xy + \left(\frac{a}{b}\right)y^2 = 0. \]

Multiplying through by \(b\) to clear the denominators, the equation becomes:

\[ bx^2 - 2hxy + ay^2 = 0. \]

Thus, the equation of the pair of straight lines perpendicular to the given pair of straight lines \(ax^2 + 2hxy + by^2 = 0\) is:

\[ bx^2 - 2hxy + ay^2 = 0. \]

This completes the proof.

Equation of a Pair of Straight Lines Parallel to a given homogenous Pair

The joint equation of a pair of straight lines intersecting at \((x_1, y_1)\) and parallel to a homogeneous pair of straight lines given by \(ax^2 + 2hxy + by^2 = 0\) is:

\[ a(x - x_1)^2 + 2h(x - x_1)(y - y_1) + b(y - y_1)^2 = 0. \]

Proof:

We derive this equation using the concept of shifting the origin. When the origin is shifted to \((h, k)\), a curve whose equation is \(f(x, y) = 0\) becomes \(f(x + h, y + k) = 0\), obtained by substituting \(x \to x + h\) and \(y \to y + k\)

Consider the pair of straight lines given by the homogeneous equation \(ax^2 + 2hxy + by^2 = 0\), passing through the origin. If we shift the origin to \((-x_1, -y_1)\), this pair of straight lines is now intersecting at \((x_1, y_1)\) and remains parallel to the original pair of lines described by \(ax^2 + 2hxy + by^2 = 0\).

The new equation, accounting for the shift in origin, is obtained by substituting \(x \to x - x_1\) and \(y \to y - y_1\) into the original equation:

\[ a(x - x_1)^2 + 2h(x - x_1)(y - y_1) + b(y - y_1)^2 = 0. \]

Thus, the joint equation of the pair of straight lines intersecting at \((x_1, y_1)\) and parallel to the given homogeneous pair of lines is:

\[ a(x - x_1)^2 + 2h(x - x_1)(y - y_1) + b(y - y_1)^2 = 0. \]

This completes the proof.

Equation of a Pair of Straight Lines Perpendicular to a Given Pair and Intersecting at a Given Point

Given the pair of straight lines represented by \(ax^2 + 2hxy + by^2 = 0\), the equation of a pair of straight lines perpendicular to this given pair and intersecting at the point \((x_1, y_1)\) is:

\[ b(x - x_1)^2 - 2h(x - x_1)(y - y_1) + a(y - y_1)^2 = 0. \]

Common Line to Pair of Lines

When one line in a pair is parallel to a line in another pair

Suppose we wish to check whether two given pairs of straight lines:

\[ a_1x^2 + 2h_1xy + b_1y^2 = 0 \quad \text{and} \quad a_2x^2 + 2h_2xy + b_2y^2 = 0 \]

have a line in common. We can determine this without actually factorizing the equations by the following condition:

If the pairs of straight lines have a line in common, then:

\[ \begin{vmatrix} a_1 & 2h_1 \\ a_2 & 2h_2 \end{vmatrix} \begin{vmatrix} 2h_1 & b_1 \\ 2h_2 & b_2 \end{vmatrix} = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}^2. \]

Proof:

Let \( y = mx \) be the common line between the two pairs of straight lines.

For the first pair of straight lines, substituting \( y = mx \) into the equation \( a_1x^2 + 2h_1xy + b_1y^2 = 0 \), we get:

\[ a_1x^2 + 2h_1x(mx) + b_1(mx)^2 = 0 \implies a_1x^2 + 2h_1mx^2 + b_1m^2x^2 = 0 \implies (a_1 + 2h_1m + b_1m^2)x^2 = 0. \]

Since \( x \neq 0 \), we have:

\[ b_1m^2 + 2h_1m + a_1 = 0. \quad \text{(1)} \]

Similarly, for the second pair of straight lines, substituting \( y = mx \) into the equation \( a_2x^2 + 2h_2xy + b_2y^2 = 0 \), we get:

\[ a_2x^2 + 2h_2x(mx) + b_2(mx)^2 = 0 \implies a_2x^2 + 2h_2mx^2 + b_2m^2x^2 = 0 \implies (a_2 + 2h_2m + b_2m^2)x^2 = 0. \]

Since \( x \neq 0 \), we have:

\[ b_2m^2 + 2h_2m + a_2 = 0. \quad \text{(2)} \]

From equations (1) and (2), we have:

\[ \frac{m^2}{\begin{vmatrix} 2h_1 & a_1 \\ 2h_2 & a_2 \end{vmatrix}} = \frac{-m}{\begin{vmatrix} b_1 & a_1 \\ b_2 & a_2 \end{vmatrix}} = \frac{1}{\begin{vmatrix} b_1 & 2h_1 \\ b_2 & 2h_2 \end{vmatrix}}. \]

Therefore,

\[ m^2 = \frac{\begin{vmatrix} 2h_1 & a_1 \\ 2h_2 & a_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ b_2 & 2h_2 \end{vmatrix}} \quad \text{and} \quad m = -\frac{\begin{vmatrix} b_1 & a_1 \\ b_2 & a_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ b_2 & 2h_2 \end{vmatrix}}. \]

Thus,

\[ \frac{\begin{vmatrix} b_1 & a_1 \\ b_2 & a_2 \end{vmatrix}^2}{\begin{vmatrix} b_1 & 2h_1 \\ b_2 & 2h_2 \end{vmatrix}%^2} = \frac{\begin{vmatrix} 2h_1 & a_1 \\ 2h_2 & a_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ b_2 & 2h_2 \end{vmatrix}} \]

Therefore,

\[ \begin{vmatrix} a_1 & 2h_1 \\ a_2 & 2h_2 \end{vmatrix} \begin{vmatrix} 2h_1 & b_1 \\ 2h_2 & b_2 \end{vmatrix} = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}^2. \]

We did some rearragement of columns in the last step using properties of determinants.

This completes the proof.

Both Lines are common

If \( a_1x^2 + 2h_1xy + b_1y^2 = 0 \) and \( a_2x^2 + 2h_2xy + b_2y^2 = 0 \) are two given pairs of straight lines, then both lines are common if and only if:

\[ \frac{a_1}{a_2} = \frac{h_1}{h_2} = \frac{b_1}{b_2}. \]

When one line in one pair is perpendicular to a line in another pair

If one of the lines represented by \(a_1x^2 + 2h_1xy + b_1y^2 = 0\) is perpendicular to one of the lines represented by \(a_2x^2 + 2h_2xy + b_2y^2 = 0\), then:

\[ \begin{vmatrix} a_1 & 2h_1 \\ -b_2 & -2h_2 \end{vmatrix} \begin{vmatrix} 2h_1 & b_1 \\ -2h_2 & a_2 \end{vmatrix} = \begin{vmatrix} a_1 & b_1 \\ b_2 & a_2 \end{vmatrix}^2. \]

Proof:

Let \( y = mx \) be the line in \( a_1x^2 + 2h_1xy + b_1y^2 = 0 \), which is perpendicular to one of the lines in \( a_2x^2 + 2h_2xy + b_2y^2 = 0 \).

Its equation is:

\[ y = -\frac{1}{m} x. \]

Substitute \( y = mx \) in \( a_1x^2 + 2h_1xy + b_1y^2 = 0 \):

\[ a_1x^2 + 2h_1x(mx) + b_1(mx)^2 = 0 \implies a_1x^2 + 2h_1mx^2 + b_1m^2x^2 = 0 \implies (a_1 + 2h_1m + b_1m^2)x^2 = 0. \]

Since \( x \neq 0 \), we have:

\[ b_1m^2 + 2h_1m + a_1 = 0. \quad \text{(1)} \]

Substitute \( y = -\frac{1}{m}x \) in \( a_2x^2 + 2h_2xy + b_2y^2 = 0 \):

\[ a_2x^2 + 2h_2x\left(-\frac{1}{m}x\right) + b_2\left(-\frac{1}{m}x\right)^2 = 0 \implies a_2x^2 - \frac{2h_2x^2}{m} + \frac{b_2x^2}{m^2} = 0 \implies a_2 - \frac{2h_2}{m} + \frac{b_2}{m^2} = 0. \]

Multiplying through by \( m^2 \), we get:

\[ m^2a_2 - 2h_2m + b_2 = 0. \quad \text{(2)} \]

From equations (1) and (2), we have:

\[ \frac{m^2}{\begin{vmatrix} 2h_1 & a_1 \\ -2h_2 & b_2 \end{vmatrix}} = \frac{-m}{\begin{vmatrix} b_1 & a_1 \\ a_2 & b_2 \end{vmatrix}} = \frac{1}{\begin{vmatrix} b_1 & 2h_1 \\ a_2 & -2h_2 \end{vmatrix}}. \]

Therefore,

\[ m^2 = \frac{\begin{vmatrix} 2h_1 & a_1 \\ -2h_2 & b_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ a_2 & -2h_2 \end{vmatrix}} \quad \text{and} \quad m = -\frac{\begin{vmatrix} b_1 & a_1 \\ a_2 & b_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ a_2 & -2h_2 \end{vmatrix}}. \]

Thus,

\[ \frac{\begin{vmatrix} b_1 & a_1 \\ a_2 & b_2 \end{vmatrix}^2}{\begin{vmatrix} b_1 & 2h_1 \\ a_2 & -2h_2 \end{vmatrix}^2} = \frac{\begin{vmatrix} 2h_1 & a_1 \\ -2h_2 & b_2 \end{vmatrix}}{\begin{vmatrix} b_1 & 2h_1 \\ a_2 & -2h_2 \end{vmatrix}} \]

Therefore,

\[ \begin{vmatrix} a_1 & 2h_1 \\ b_2 & -2h_2 \end{vmatrix} \begin{vmatrix} 2h_1 & b_1 \\ -2h_2 & a_2 \end{vmatrix} = \begin{vmatrix} a_1 & b_1 \\ b_2 & a_2 \end{vmatrix}^2. \]

Rearranging, we get the required result.