Properties of Conjugate and Modulus of a Complex Number
Introduction
The conjugate, modulus, and argument of a complex number are interconnected concepts that play crucial roles in complex number theory. The conjugate of a complex number \(z = a + bi\) is \( \overline{z} = a - bi \), essentially mirroring \(z\) across the real axis. The modulus, \( |z| \), represents the distance of \(z\) from the origin in the complex plane and is calculated as \( \sqrt{a^2 + b^2} \). The argument, often denoted as \( \arg(z) \), is the angle \( \theta \) that the line connecting \(z\) to the origin makes with the positive real axis, measured in radians. The modulus and argument together describe the position of \(z\) in polar coordinates. Notably, the modulus of \(z\) and its conjugate \( \overline{z} \) are the same, as they are equidistant from the origin. The argument of \( \overline{z} \) is the negative of the argument of \(z\), reflecting the symmetry across the real axis. These properties highlight the deep interrelation between the algebraic and geometric aspects of complex numbers, facilitating their manipulation and understanding in both algebraic operations and geometric interpretations.
Properties of conjugate
For a complex number \( z \), let \( \overline{z} \) denote its conjugate. The properties and corresponding proofs involving complex numbers and their conjugates are as follows:
-
Double Conjugate Property: \( \overline{\overline{z}} = z \)
-
Conjugation and Real and Imaginary Parts:
- \(z + \overline{z} = 2\text{Re}(z)\)
- \(z - \overline{z} = 2i\text{Im}(z)\)
Thus, \( z + \overline{z} = 0 \) if and only if \( z \) is purely imaginary, and \( z = \overline{z} \) if and only if \( z \) is real.
Proof:
Let \( z = a + bi \) where \( a, b \in \mathbb{R} \) and \( i \) is the imaginary unit. Then the conjugate of \( z \), denoted \( \overline{z} \), is \( a - bi \).
\( z + \overline{z} = (a + bi) + (a - bi) = a + a = 2a = 2\text{Re}(z)\)
\(z - \overline{z} = (a + bi) - (a - bi) = bi + bi = 2bi = 2i\text{Im}(z)\)
For the implications:
If \( z + \overline{z} = 0 \), then \( 2\text{Re}(z) = 0 \) implying \( \text{Re}(z) = 0 \). Therefore, \( z \) is purely imaginary since \( z = a + bi \) with \( a = 0 \).
Conversely, if \( z \) is purely imaginary, then \( a = 0 \) and \( z = bi \). Therefore, \( z + \overline{z} = bi - bi = 0 \).
If \( z = \overline{z} \), then \( a + bi = a - bi \) implying \( bi = -bi \), which is true if and only if \( b = 0 \). Thus, \( z \) is a real number since \( z = a + 0i \).
Conversely, if \( z \) is real, then \( z = a \) and \( \overline{z} = a \) which means \( z = \overline{z} \).
In summary, \( z \) is purely imaginary if and only if \( z + \overline{z} = 0 \), and \( z \) is real if and only if \( z = \overline{z} \).
-
Modulus Property: \( z\overline{z} = |z|^2 \).
Proof: If \( z = a + bi \), then \( \overline{z} = a - bi \) and thus \( z\overline{z} = (a + bi)(a - bi) = a^2 + b^2 = |z|^2 \).
An Important Special Case
Let \( z \) be a complex number with \( |z| = 1 \). Then \( z\overline{z} = |z|^2 \). Since \( |z| = 1 \), it follows that:
\[z\overline{z} = 1.\]Therefore, the complex conjugate \( \overline{z} \) is the multiplicative inverse of \( z \):
\[ \overline{z} = \frac{1}{z}. \] -
Summation Property: \( \overline{z_1 + z_2} = \overline{z_1} + \overline{z_2} \).
Proof: Let \( z_1 = a + bi \), \( z_2 = c + di \), then \( \overline{z_1 + z_2} = \overline{(a + bi) + (c + di)} = \overline{(a + c) + (b + d)i} = (a + c) - (b + d)i = \overline{z_1} + \overline{z_2} \).
-
Product Property:\( \overline{z_1z_2} = \overline{z_1} \cdot \overline{z_2} \).
Proof: Using the definition of complex multiplication, \( \overline{z_1z_2} = \overline{(a + bi)(c + di)} = \overline{(ac - bd) + (bc + ad)i} = (ac - bd) - (bc + ad)i = \overline{z_1} \cdot \overline{z_2} \).
-
Division Property:\( \frac{\overline{z_1}}{z_2} = \frac{\overline{z_1}}{\overline{z_2}} \), provided \( z_2 \neq 0 \).
Proof: Multiply numerator and denominator by \( \overline{z_2} \): \( \frac{\overline{z_1}}{z_2} = \frac{\overline{z_1} \cdot \overline{z_2}}{z_2 \cdot \overline{z_2}} = \frac{\overline{z_1}}{\overline{z_2}} \), since \( z_2\overline{z_2} = |z_2|^2 \).
-
\( |z| = |\overline{z}| \).
Proof: \( |\overline{z}|^2 = \overline{z} \cdot z = |z|^2 \), hence \( |z| = |\overline{z}| \).
-
Argument Property: \( \text{arg}(\overline{z}) = -\text{arg}(z) \).
Proof: If \( z = re^{i\theta} \), then \( \overline{z} = re^{-i\theta} \), implying \( \text{arg}(\overline{z}) = -\theta = -\text{arg}(z) \).
An Important theorem as a consequence of above properties
Theorem: The square of the modulus of the sum of two complex numbers \( z_1 \) and \( z_2 \) is equal to the sum of the squares of their moduli plus twice the real part of the product of the first number and the conjugate of the second. Formally, this is stated as:
Proof: Let \( z_1 \) and \( z_2 \) be complex numbers. The modulus squared of their sum is given by the product of \( z_1 + z_2 \) and its conjugate \( \overline{z_1 + z_2} \). Expanding this product, we have:
Notice that \( z_1\overline{z_2} \) and \( \overline{z_1}z_2 \) are conjugates of each other. Therefore, their sum is twice the real part of either:
Substituting this into our previous equation, we obtain:
Hence, the theorem is proved. \(\blacksquare\)
Similarly, for the difference:
\( |z_1 - z_2|^2 = (z_1 - z_2)(\overline{z_1} - \overline{z_2}) \) \( = z_1\overline{z_1} - z_1\overline{z_2} - z_2\overline{z_1} + z_2\overline{z_2} \) \( = |z_1|^2 - z_1\overline{z_2} - \overline{z_1}z_2 + |z_2|^2 \) \( = |z_1|^2 + |z_2|^2 - 2\text{Re}(z_1\overline{z_2}) \).
Properties of Modulus
Some important properties of the Modulus of a complex number:
-
\( \|z\| = |z| \)
-
\( |z| = |\overline{z}| \)
-
\( |-z| = |z| \)
-
\( |kz| = |k||z| \) for any real number \( k \)
-
\( |z_1z_2| = |z_1||z_2| \)
Proof of Property 5:
Let \( z_1 = x_1 + iy_1 \) and \( z_2 = x_2 + iy_2 \).
Then,
\[ \begin{align*} z_1z_2 &= (x_1 + iy_1)(x_2 + iy_2) \\ &= (x_1x_2 - y_1y_2) + i(x_1y_2 + y_1x_2), \end{align*} \]and so,
\[ \begin{align*} |z_1z_2| &= \sqrt{(x_1x_2 - y_1y_2)^2 + (x_1y_2 + y_1x_2)^2} \\ &= \sqrt{x_1^2x_2^2 + y_1^2y_2^2 - 2x_1x_2y_1y_2 + x_1^2y_2^2 + y_1^2x_2^2 + 2x_1y_2y_1x_2} \\ &= \sqrt{x_1^2(x_2^2 + y_2^2) + y_1^2(x_2^2 + y_2^2)} \\ &= \sqrt{(x_1^2 + y_1^2)(x_2^2 + y_2^2)} \\ &= \sqrt{x_1^2 + y_1^2} \sqrt{x_2^2 + y_2^2} \\ &= |z_1||z_2|. \end{align*} \]This completes the proof that the modulus of the product of two complex numbers is equal to the product of their moduli.\(\blacksquare\)
An useful identity from the above proof
\[ (ac \pm bd)^2 + (ad \mp bc)^2 = (a^2 + b^2)(c^2 + d^2) \]This can be proved as follows:
Consider the left-hand side of the equation:
\[ (ac \pm bd)^2 + (ad \mp bc)^2 \]Expanding both squares, we have:
\[ (ac \pm bd)^2 = a^2c^2 \pm 2abcd + b^2d^2 \]\[ (ad \mp bc)^2 = a^2d^2 \mp 2abcd + b^2c^2 \]Adding these expansions together:
\[ a^2c^2 \pm 2abcd + b^2d^2 + a^2d^2 \mp 2abcd + b^2c^2 \]Notice that \( \pm 2abcd \) and \( \mp 2abcd \) cancel each other out, so we are left with:
\[ a^2c^2 + a^2d^2 + b^2d^2 + b^2c^2 \]Factor by grouping \( a^2 \) and \( b^2 \):
\[ a^2(c^2 + d^2) + b^2(c^2 + d^2) \]This can be further factored to get the right-hand side of the original equation:
\[ (a^2 + b^2)(c^2 + d^2) \]Thus proving the original assertion.
-
\(\left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|}\)
-
\(-|z| \leq \text{Re}(z) \leq |z|\) and \(-|z| \leq \text{Im}(z) \leq |z|\)
Proof of Property 7:
Let \( z \) be a complex number, such that \( z = a + bi \) where \( a = \text{Re}(z) \) and \( b = \text{Im}(z) \).
The modulus of \( z \) is given by \( |z| = \sqrt{a^2 + b^2} \).
The square of the modulus is \( |z|^2 = a^2 + b^2 \).
Since \( b^2 \) is non-negative (as it is a square), it follows that \( a^2 \leq a^2 + b^2 \), and thus \( |a| \leq |z| \). This implies both \( a \leq |z| \) and \( -a \leq |z| \), or equivalently, \( -|z| \leq a \).
Since \( a = \text{Re}(z) \), we have \( -|z| \leq \text{Re}(z) \leq |z| \).
Similarly, since \( a^2 \) is non-negative, \( b^2 \leq a^2 + b^2 \), which gives \( |b| \leq |z| \). Hence, \( -|z| \leq b \) and \( b \leq |z| \), or \( -|z| \leq \text{Im}(z) \leq |z| \).
\(\blacksquare\)
Triangle's Inequality
Triangle Inequality Theorem for Complex Numbers:
For any complex numbers \( z_1 \) and \( z_2 \), the following inequalities hold:
-
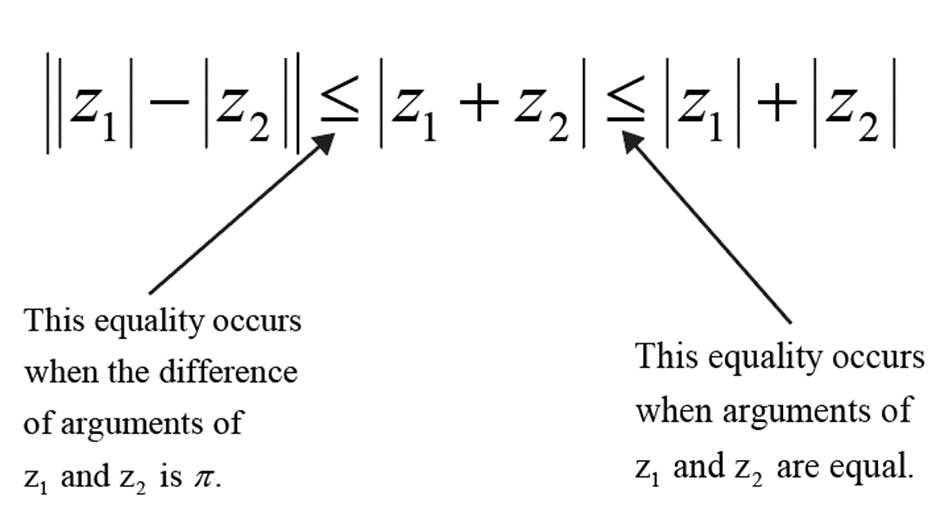
The left inequality becomes an equality if and only if the difference in the arguments of \( z_1 \) and \( z_2 \) is \( \pi \). This corresponds to \( z_1 \) and \( z_2 \) being diametrically opposite points on the complex plane.
-
The right inequality becomes an equality if and only if the arguments of \( z_1 \) and \( z_2 \) are equal. This corresponds to \( z_1 \) and \( z_2 \) pointing in the same direction on the complex plane.
Geometric Proof:
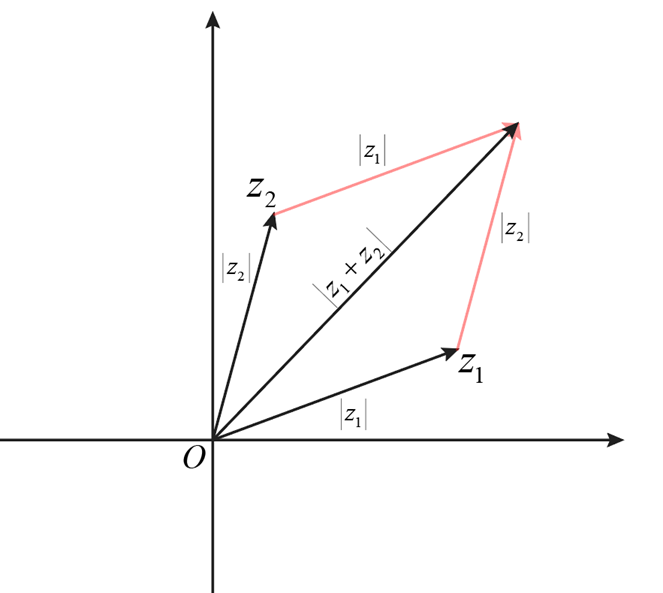
In the complex plane, the complex numbers \( z_1 \) and \( z_2 \) can be represented by points A and B, respectively. The sum \( z_1 + z_2 \) is represented by point C, which is the endpoint of the diagonal of the parallelogram OACB, with O as the origin.
To prove the right inequality \( |z_1 + z_2| \leq |z_1| + |z_2| \):
Observe triangle OAC. By the triangle inequality in geometry (not to be confused with the Triangle Inequality Theorem for complex numbers), the sum of the lengths of two sides of a triangle is greater than or equal to the length of the third side. Hence, \( OA + AC \geq OC \), which translates to \( |z_1| + |z_2| \geq |z_1 + z_2| \).
The equality \( |z_1 + z_2| = |z_1| + |z_2| \) occurs only when points A, B, and O are collinear and OA ans OB have the same direction, which happens when \( z_1 \) and \( z_2 \) lie on the same ray from the origin, meaning they have the same argument.
To prove the left inequality \( ||z_1| - |z_2|| \leq |z_1 + z_2| \):
First, consider triangle OCB. Using the triangle inequality, \( OC + OB \geq BC \), or \( OC \geq OB - OC \). Translating this to complex numbers, \( |z_1 + z_2| \geq |z_2| - |z_1| \).
Next, observe triangle OAC. Again applying the triangle inequality, \( OA + OC \geq AC \), or \( OC \geq OA - OC \). In terms of complex numbers, this is \( |z_1 + z_2| \geq |z_1| - |z_2| \).
Combining both results, we conclude that \( |z_1 + z_2| \geq ||z_1| - |z_2|| \), meaning the modulus of the sum is greater than or equal to the absolute difference of the moduli.
The equality \( |z_1 + z_2| = ||z_1| - |z_2|| \) occurs when points A, B, and O are collinear and OA and OB are in opposite directions. This scenario happens when \( z_1 \) and \( z_2 \) lie on rays in opposite directions, which means their arguments differ by \( \pi \).
Thus, the geometrical interpretation of the complex plane and the properties of triangles provide a convincing proof of the Triangle Inequality Theorem for complex numbers.
The image contains a two-part algebraic proof concerning the modulus of a complex number and its components, using properties of the real and imaginary parts. Here is the transcription of the proof provided in the images:
Algebraic proof
If \( z_1 = x_1 + iy_1 \) and \( z_2 = x_2 + iy_2 \), then
Let us do some analysis of the third term of the above identity.
Now using the inequality, \( -|z| \leq \text{Re}(z) \leq |z| \), where equality on the right side occurs when occurs when imaginary part is zero and the real part is positive and the equality on the left side occurs when imaginary part is zero and the real part is negative.
Equality on the right side occurs when imaginary part of \( z_1\overline{z_2} \) is zero and its real part is positive.
\( z_1\overline{z_2} = (x_1 + iy_1)(x_2 - iy_2) \)
Clearly,
\( \text{Im}(z_1\overline{z_2}) = y_1x_2 - x_1y_2 \)
The line joining origin to \( (x_1, y_1) \) and the line joining origin to \( (x_2, y_2) \) have the same slope, which suggests that either they are in the same quadrant or the opposite quadrant.
Now, \( \text{Re}(z_1\overline{z_2}) > 0 \) implies \( x_1x_2 + y_1y_2 > 0 \) implying \( (x_1, y_1) \) and \( (x_2, y_2) \) are in the same quadrant. Also, \( \text{Re}(z_1\overline{z_2}) < 0 \) implies \( x_1x_2 + y_1y_2 < 0 \) implying \( (x_1, y_1) \) and \( (x_2, y_2) \) are in the opposite quadrant
Finally, we can conclude that when equality occurs on the right side, arguments of \( z_1 \) and \( z_2 \) are the same, but when equality occurs on the left side, arguments of \( z_1 \) and \( z_2 \) differ by an angle \( \pi \).
We can now go back to (1). Using the result of (2), we can say that
(Using the fact that \( a^2 \leq x^2 \leq b^2 \) implies \( |a| \leq |x| \leq |b| \). Since \( |z_1 + z_2| \) and \( |z_1| + |z_2| \) are always positive we have removed the useless modulus symbol, but \( |z_1| - |z_2| \) may be positive or negative, that’s why we have not removed it.)
Info
We will call the right inequality: \( |z_1 + z_2| \leq |z_1| + |z_2|\) as First Triangle's Inequality and the left one: \(||z_1| - |z_2|| \leq |z_1 + z_2|\) as Second or Reverse Triangle's Inequality.
The Second Triangle Inequality for complex numbers \( z_1 \) and \( z_2 \) can be obtained from the First Triangle Inequality by considering the complex number \(-z_2\) instead of \(z_2\):
Using the First Triangle Inequality \( |z_1 + z_2| \leq |z_1| + |z_2| \), and replacing \( z_2 \) with \( -z_2 \), we get:
Since \( |-z| = |z| \) for any complex number \( z \), we can rewrite this as:
The equality occurs only when \(z_1\) and \(z_2\) lie on rays in opposite directions, that is, the difference of arguments is \(pi\).
Similarly, we get:
Equality occurs when \( z_1 \) and \( z_2 \) lie on rays in the same direction, meaning their arguments are equal.
Application of Triangle's Inequalities
One of the main usage of these inequalities is in calculation of minimum and maximum values of expressions involving complex numbers. Consider the following examples:
Example
Problem: Given a complex number \( z \) that satisfies \( |z| = 4 \), find the maximum value of \( |z - 3 - 4i| \).
Solution: To find the maximum value of \( |z - 3 - 4i| \), we can use the Triangle Inequality, which states that for any two complex numbers \( z_1 \) and \( z_2 \), \( |z_1 + z_2| \leq |z_1| + |z_2| \). By applying the Triangle Inequality to the expression \( |z - (3 + 4i)| \), we get:
Since \( |z| = 4 \) and \( |3 + 4i| = 5 \)
Therefore, the maximum value of \( |z - 3 - 4i| \) is \( 9 \).
Example
Problem: Given a complex number \( z \) satisfying \( |z - 2| \leq 3 \), find the maximum value of \( |z + i| \).
Solution: Start by expressing \( |z + i| \) in terms of \( |z - 2| \):
By applying the Triangle Inequality, which states that \( |a + b| \leq |a| + |b| \) for any two complex numbers \( a \) and \( b \), we get:
Since \( |2 + i| = \sqrt{2^2 + 1^2} = \sqrt{5} \), the inequality simplifies to:
because \( |z - 2| \leq 3 \), we get,
[ |z + i| \leq |z - 2| + \sqrt{5} \leq 3 + \sqrt{5}]
Thus, the maximum value of \( |z + i| \) is \( 3 + \sqrt{5} \).
Example
Problem: Given a complex number \(z\) such that \( |z - 1| \geq 5 \), find the minimum value of \( |z - 2i| \).
Solution: We can use the Reverse Triangle Inequality, which states that for any two complex numbers \( a \) and \( b \), \( ||a| - |b|| \leq |a + b| \). To find the minimum value of \( |z - 2i| \), we rewrite it in terms of \( |z - 1| \):
Using the Reverse Triangle Inequality, we have:
Now, we know that \( |z - 1| > 5 \), so we can substitute this inequality into our expression:
We know that,
So we continue:
Since \( 5 - \sqrt{5} \) is positive (as \( 5 > \sqrt{5} \)), the absolute value is not needed:
Thus, the minimum value of \( |z - 2i| \) is \( 5 - \sqrt{5} \). \(\blacksquare\)
Example
Problem: Let \( z \) be a complex number such that \( |z| = r \), where \( r > 0 \). Find the minimum and maximum values of \( |z + \frac{1}{z}| \).
Solution:
To find the maximum value of \( |z + \frac{1}{z}| \), we apply the First Triangle Inequality:
Since \( |z| = r \) and \( \left|\frac{1}{z}\right| = \frac{1}{|z|} = \frac{1}{r} \), we have:
This is the maximum value of \( |z + \frac{1}{z}| \).
To find the minimum value of \( |z + \frac{1}{z}| \), we apply the Second Triangle Inequality:
Using the given that \( |z| = r \), we have:
If \( r \geq 1 \), then \( r - \frac{1}{r} \) is positive, and we have:
If \( r < 1 \), then \( r - \frac{1}{r} \) is negative, and we must take the absolute value:
Since \( r > 0 \), the minimum value of \( |z + \frac{1}{z}| \) is \( \left|r - \frac{1}{r}\right| \), regardless of whether \( r \geq 1 \) or \( r < 1 \).
Thus, the minimum value of \( |z + \frac{1}{z}| \) is \( \left|r - \frac{1}{r}\right| \), and the maximum value is \( r + \frac{1}{r} \). \(\blacksquare\)
Example
Problem:
Find the range of \( |z| \) given that \( |z + \frac{1}{z}| = r \), where \( r \) is a positive real number.
Solution:
We know that,
Let us first solve: \( |z + \frac{1}{z}| \leq |z| + \left|\frac{1}{z}\right| \)
We have \( |z| + \left|\frac{1}{z}\right| \geq r \)
This implies that \( |z|^2 - r|z| + 1 \geq 0 \), which leads to \( |z| \geq \frac{r + \sqrt{r^2 - 4}}{2} \) or \( 0 \leq |z| \leq \frac{r - \sqrt{r^2 - 4}}{2} \) (Clearly this is true only when \( r \geq 2 \))
If \( r < 2 \), then \( |z| > 0 \)
Now let us solve \( \left| |z| - \left|\frac{1}{z}\right| \right| \leq r \) implies \( -r \leq |z| - \left|\frac{1}{z}\right| \leq r \)
The above inequality can be solved as
Combining the result (which requires a little more algebra, try!):
For \( r \leq 2 \),
For \( r > 2 \),
More properties
-
\[ |z_1 + z_2| = |z_1 - z_2| \implies O_{z_1} \perp O_{z_2} \]
This relation can be deduced from the geometric representation.
The algebraic proof is even more important here.
Take the square of both sides,
\[ |z_1 + z_2|^2 = |z_1 - z_2|^2 \]This implies
\[ (z_1 + z_2)(\overline{z_1} + \overline{z_2}) = (z_1 - z_2)(\overline{z_1} - \overline{z_2}) \quad [\text{Using } zz = |z|^2 ] \]This expands to
\[ z_1\overline{z_1} + z_2\overline{z_2} + z_1\overline{z_2} + z_2\overline{z_1} = z_1\overline{z_1} + z_2\overline{z_2} - z_1\overline{z_2} - z_2\overline{z_1} \]Simplifying,
\[ |z_1|^2 + |z_2|^2 + 2z_1\overline{z_2} + 2z_2\overline{z_1} = |z_1|^2 + |z_2|^2 - 2z_1\overline{z_2} - 2z_2\overline{z_1} \]Thus,
\[ 2z_1\overline{z_2} + 2z_2\overline{z_1} = 0 \]Which simplifies to
\[ z_1\overline{z_2} = -z_2\overline{z_1} \]This can be rewritten as
\[ \frac{z_1}{z_2} = -\frac{\overline{z_1}}{\overline{z_2}} \]Thus, we have
\[ \frac{z_1}{z_2} = -\overline{\left( \frac{z_1}{z_2} \right)} \]Therefore,
\[ \frac{z_1}{z_2} \text{ is purely imaginary} \quad \Rightarrow \text{ angle between } O_{z_1} \text{ and } O_{z_2} \text{ is } \frac{\pi}{2}. \]This concludes the algebraic proof showing that if the modulus of the sum is equal to the modulus of the difference of two complex numbers, the vectors representing these complex numbers in the complex plane are perpendicular to each other.
\(\frac{z_1}{z_2} \text{ is purely imaginary} \quad \Rightarrow \text{ angle between } O_{z_1} \text{ and } O_{z_2} \text{ is } \frac{\pi}{2}. \)
Given \( z_1 = a_1 + ib_1 \) and \( z_2 = a_2 + ib_2 \), let's consider what it means for \( \frac{z_1}{z_2} \) to be purely imaginary.
The division of \( z_1 \) by \( z_2 \) is:
\[ \frac{z_1}{z_2} = \frac{a_1 + ib_1}{a_2 + ib_2} \]Multiplying numerator and denominator by the conjugate of the denominator to make the denominator real:
\[ \frac{z_1}{z_2} = \frac{(a_1 + ib_1)(a_2 - ib_2)}{a_2^2 + b_2^2} \]\[ \frac{z_1}{z_2} = \frac{a_1a_2 + b_1b_2}{a_2^2 + b_2^2} + i\frac{a_2b_1 - a_1b_2}{a_2^2 + b_2^2} \]For \( \frac{z_1}{z_2} \) to be purely imaginary, the real part must be zero:
\[ \frac{a_1a_2 + b_1b_2}{a_2^2 + b_2^2} = 0 \]\[ a_1a_2 + b_1b_2 = 0 \]Now, we interpret \( a_1, b_1 \) and \( a_2, b_2 \) as coordinates of points \( z_1 \) and \( z_2 \) in the complex plane, representing vectors \( O_{z_1} \) and \( O_{z_2} \). In vector terms, this implies that the dot product of \( O_{z_1} \) and \( O_{z_2} \) is zero, which is a condition for perpendicularity.
Alternatively, the equation \( a_1a_2 + b_1b_2 = 0 \) can be rewritten to express the slopes of lines \( O_{z_1} \) and \( O_{z_2} \):
\[ \frac{b_1}{a_1}.\frac{b_2}{a_2} =-1\]Thus, the product of slopes of the lines from the origin to \( z_1 \) and \(z_2\) is \(-1\) . In a Cartesian coordinate system, if the product of the slopes of two lines is -1, the lines are perpendicular.
Therefore, \( O_{z_1} \) is perpendicular to \( O_{z_2} \), meaning the angle between them is \( 90^\circ \) or \( \frac{\pi}{2} \) radians.
If you do not know the concept of slopes of straightn lines, you can totally ignore this proof for a while. A more straightforward proof will soon follow.
-
\( |z_1 + z_2|^2 = |z_1|^2 + |z_2|^2 \Rightarrow O_{z_1} \perp O_{z_2} \)
proof
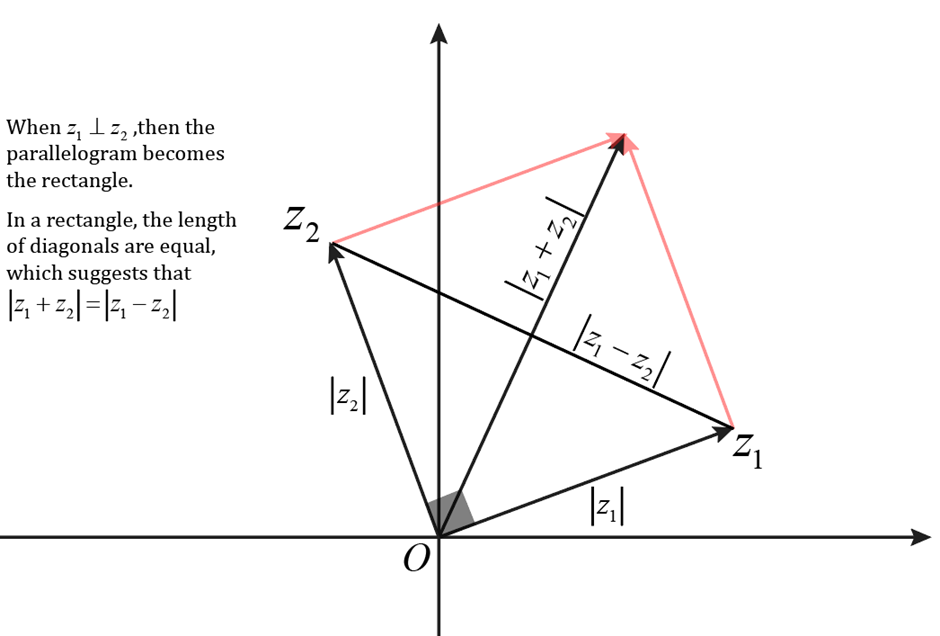
In the complex plane, \( |z_1 + z_2| \) and \( |z_1 - z_2| \) are the lengths of the diagonals of the parallelogram formed by \( z_1 \) and \( z_2 \).
From the parallelogram law, if \( z_1 \) is perpendicular to \( z_2 \), the parallelogram formed is a rectangle. In a rectangle, the diagonals are equal in length, which aligns with the equation given:
\[ |z_1 + z_2| = |z_1 - z_2| \]Now, if we apply the Pythagorean theorem to the right-angled triangle formed by \( z_1 \), \( z_2 \), and \( z_1 + z_2 \) (or \( z_1 - z_2 \)), we have:
\[ |z_1|^2 + |z_2|^2 = |z_1 + z_2|^2 \]This is only true if \( z_1 \) and \( z_2 \) are perpendicular to each other because for right-angled triangles, the square of the length of the hypotenuse (the diagonal in our case) is equal to the sum of the squares of the other two sides (the vectors \( z_1 \) and \( z_2 \)).
Therefore, by observing the given figure and using the properties of a parallelogram and the Pythagorean theorem, we can conclude that \( O_{z_1} \) is perpendicular to \( O_{z_2} \).
-
Given \( a \) and \( b \) are real numbers and \( z_1 \) and \( z_2 \) are complex numbers, let's prove the given identity:
\[ |az_1 + bz_2|^2 + |bz_1 - az_2|^2 = (a^2 + b^2)(|z_1|^2 + |z_2|^2) \]Proof:
We expand the left-hand side (LHS) using \( |z|^2 = zz^* \), where \( z^* \) denotes the complex conjugate of \( z \).
For the first term \( |az_1 + bz_2|^2 \):
\[ |az_1 + bz_2|^2 = (az_1 + bz_2)(a\overline{z_1} + b\overline{z_2}) \]\[ = a^2z_1\overline{z_1} + abz_1\overline{z_2} + abz_2\overline{z_1} + b^2z_2\overline{z_2} \]\[ = a^2|z_1|^2 + ab(z_1\overline{z_2} + z_2\overline{z_1}) + b^2|z_2|^2 \]For the second term \( |bz_1 - az_2|^2 \):
\[ |bz_1 - az_2|^2 = (bz_1 - az_2)(b\overline{z_1} - a\overline{z_2}) \]\[ = b^2z_1\overline{z_1} - abz_1\overline{z_2} - abz_2\overline{z_1} + a^2z_2\overline{z_2} \]\[ = b^2|z_1|^2 - ab(z_1\overline{z_2} + z_2\overline{z_1}) + a^2|z_2|^2 \]Adding the two expansions together, the mixed terms \( ab(z_1\overline{z_2} + z_2\overline{z_1}) \) will cancel out, yielding:
\[ a^2|z_1|^2 + b^2|z_2|^2 + b^2|z_1|^2 + a^2|z_2|^2 \]\[ = a^2(|z_1|^2 + |z_2|^2) + b^2(|z_1|^2 + |z_2|^2) \]\[ = (a^2 + b^2)(|z_1|^2 + |z_2|^2) \]This completes the proof that the original identity holds true.
Parallelogram identity
When \( a = 1 \) and \( b = 1 \), the identity simplifies to:
\[ |z_1 + z_2|^2 + |z_1 - z_2|^2 = (1^2 + 1^2)(|z_1|^2 + |z_2|^2) \]Simplifying further gives us:
\[ |z_1 + z_2|^2 + |z_1 - z_2|^2 = 2(|z_1|^2 + |z_2|^2) \]This is an instance of the parallelogram law in complex numbers, which states that the sum of the squares of the lengths of the diagonals of a parallelogram is equal to the sum of the squares of the lengths of all sides.