Angle Bisectors

Angle Bisectors of Two Intersecting Lines

Consider two straight lines:

\[ L_1: a_1 x + b_1 y + c_1 = 0 \]

\[ L_2: a_2 x + b_2 y + c_2 = 0 \]

Suppose these lines intersect at a point \(P\).

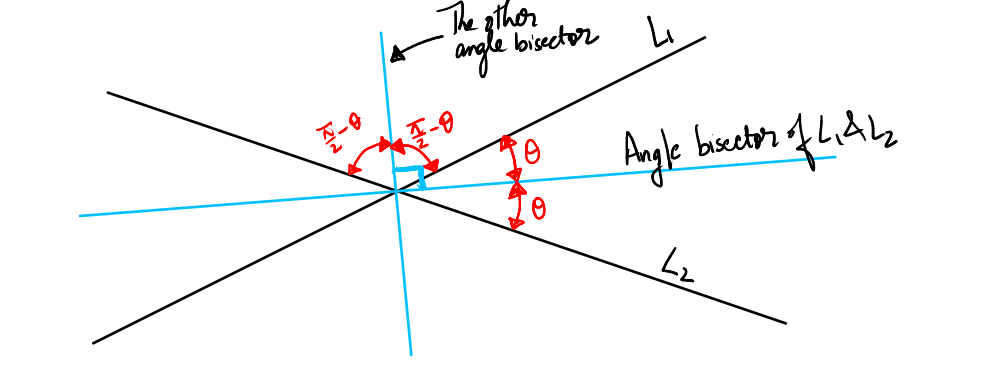
An angle bisector of \(L_1\) and \(L_2\) is a line that passes through the point \(P\) and divides the angle between \(L_1\) and \(L_2\) into two equal parts.

There are two angle bisectors for these lines: one that bisects the acute angle between \(L_1\) and \(L_2\), and another that bisects the obtuse angle, being perpendicular to the first.

The equations of the angle bisectors can be expressed as:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

This formula captures both angle bisectors: the positive sign corresponds to one bisector, and the negative sign corresponds to the other bisector.

The accompanying diagram visually demonstrates the angle bisectors of \(L_1\) and \(L_2\). These bisectors intersect the lines at the point \(P\) and split the angles formed by the intersection into two equal angles, clearly illustrating their geometric properties.

Proof

Any point on either of the angle bisectors of \(L_1\) and \(L_2\) satisfies the condition that it is equidistant from \(L_1\) and \(L_2\). Using this property, we can derive the equations of the angle bisectors.

Let \(P\) be a point \((x, y)\) lying on either of the angle bisectors. Then the distance of \(P\) from \(L_1\) and \(L_2\) must be equal.

The distance of \(P\) from \(L_1\) is:

\[ \frac{|a_1 x + b_1 y + c_1|}{\sqrt{a_1^2 + b_1^2}} \]

The distance of \(P\) from \(L_2\) is:

\[ \frac{|a_2 x + b_2 y + c_2|}{\sqrt{a_2^2 + b_2^2}} \]

Since \(P\) lies on the angle bisector, these distances must be equal:

\[ \frac{|a_1 x + b_1 y + c_1|}{\sqrt{a_1^2 + b_1^2}} = \frac{|a_2 x + b_2 y + c_2|}{\sqrt{a_2^2 + b_2^2}} \]

This implies:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

Therefore, the equations of the angle bisectors are given by:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

This formulation captures both angle bisectors: the positive sign corresponds to one bisector, and the negative sign corresponds to the perpendicular bisector.

Distinguishing Acute and Obtuse Angle Bisectors

From the formula for the angle bisectors, we obtain two equations. One corresponds to the acute angle bisector, and the other to the obtuse angle bisector. In problems, it is often necessary to determine which equation represents which bisector. Let us explore how to distinguish between them.

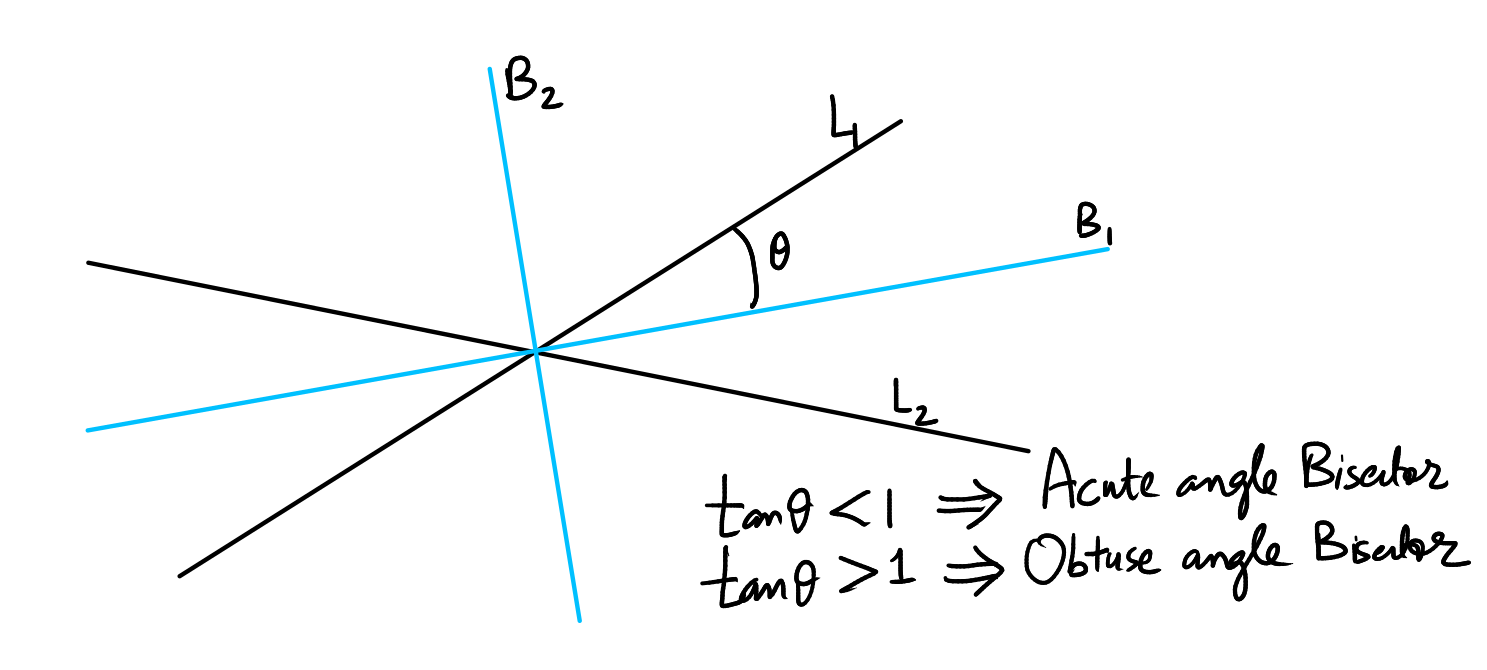
One simple method is based on the following idea: Let \( B_1 \) and \( B_2 \) be the bisectors of \( L_1 \) and \( L_2 \). Find the angle between any one of the bisectors and one of the lines, say \( B_1 \) and \( L_1 \).

If this angle is less than \( 45^\circ \), then \( B_1 \) must be the acute angle bisector, and correspondingly, \( B_2 \) is the obtuse angle bisector. Conversely, if this angle is greater than \( 45^\circ \), \( B_1 \) is the obtuse angle bisector, and \( B_2 \) is the acute angle bisector.

Since we typically calculate angles using the tangent formula, we can rephrase this method. If the tangent of the angle between \( B_1 \) and \( L_1 \) is less than 1, then \( B_1 \) is the acute angle bisector. If the tangent is greater than 1, \( B_1 \) is the obtuse angle bisector.

This approach provides a straightforward way to determine which bisector equation corresponds to the acute or obtuse angle bisector.

Example

Find the angle bisectors of the lines \( L_1: 7x + y - 3 = 0 \) and \( L_2: x - y + 4 = 0 \). Determine which of these bisectors is the acute angle bisector.

Solution:

First, we find the equations of the angle bisectors.

The angle bisectors are given by the formula:

\[ \frac{7x + y - 3}{\sqrt{7^2 + 1^2}} = \pm \frac{x - y + 4}{\sqrt{1^2 + (-1)^2}} \]

Simplify the denominators:

\[ \frac{7x + y - 3}{\sqrt{49 + 1}} = \pm \frac{x - y + 4}{\sqrt{1 + 1}} \implies \frac{7x + y - 3}{5\sqrt{2}} = \pm \frac{x - y + 4}{\sqrt{2}} \]

Multiply both sides by \(\sqrt{2}\):

\[ \frac{7x + y - 3}{5} = \pm (x - y + 4) \]

This gives us two equations:

\[ 7x + y - 3 = 5(x - y + 4) \quad \text{or} \quad 7x + y - 3 = -5(x - y + 4) \]

Solving these equations, we get:

For the positive sign:

\[ 7x + y - 3 = 5x - 5y + 20 \implies 2x + 6y - 23 = 0 \]

For the negative sign:

\[ 7x + y - 3 = -5x + 5y - 20 \implies 12x - 4y + 17 = 0 \]

Hence, the equations of the bisectors are:

\[ 2x + 6y - 23 = 0 \quad \text{and} \quad 12x - 4y + 17 = 0 \]

Now, we need to determine which bisector corresponds to the acute angle.

Determine the Acute Angle Bisector:

Choose one of the original lines and one of the bisectors to find the angle between them.

Let us choose:

• Line \( L_2: x - y + 4 = 0 \)
• Bisector: \( 2x + 6y - 23 = 0 \)

Calculate the slopes:

• Slope of the line \( L_2 \): \( 1 \)
• Slope of the bisector \( 2x + 6y - 23 = 0 \): \( -\frac{1}{3} \)

Find the tangent of the angle between them:

\[ \tan \theta = \left| \frac{1 - (-\frac{1}{3})}{1 + 1(-\frac{1}{3})} \right| \implies \left| \frac{1 + \frac{1}{3}}{1 - \frac{1}{3}} \right| \implies \left| \frac{\frac{4}{3}}{\frac{2}{3}} \right| = 2 \]

Since \( \tan \theta > 1 \), the angle between the chosen line and the bisector is greater than \( 45^\circ \). Therefore, \( 2x + 6y - 23 = 0 \) is the obtuse angle bisector.

Consequently, the other bisector, \( 12x - 4y + 17 = 0 \), must be the acute angle bisector.

Thus, the acute angle bisector is:

\[ 12x - 4y + 17 = 0 \]

Location of the Origin with Respect to Two Intersecting Lines

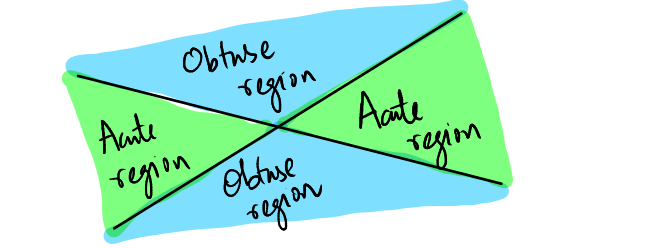
Two intersecting lines divide the Cartesian coordinate system into two distinct regions: the acute angle region and the obtuse angle region.

The acute angle region is formed by the smaller angle at the intersection of the two lines, while the obtuse angle region is formed by the larger angle. These regions are visually represented in the diagram below:

• The acute angle regions are shaded in green.
• The obtuse angle regions are shaded in blue.

Understanding the location of the origin within these regions is crucial for various geometric and algebraic analyses. In this section, we will explore how to determine whether the origin lies in the acute or obtuse region based on the equations of the intersecting lines.

To determine whether the origin lies in the acute or obtuse region formed by the intersection of two lines, consider the given lines:

\[ L_1: a_1 x + b_1 y + c_1 = 0 \]

\[ L_2: a_2 x + b_2 y + c_2 = 0 \]

Assume that \( c_1 \) and \( c_2 \) are negative. If they are not you can always make them negative by multiplying equations with -1.

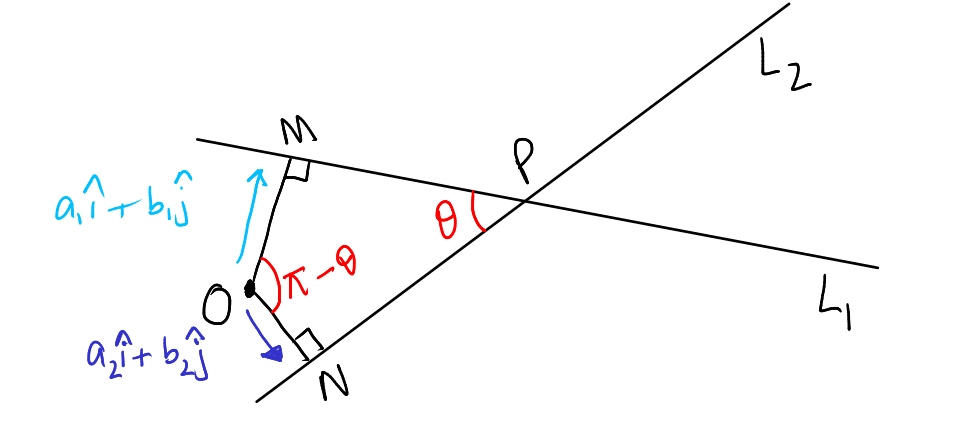
Suppose the origin lies in the acute region. To understand this, we can analyze the geometric configuration of the lines and their angle bisectors. Drop perpendiculars \( OM \) and \( ON \) from the origin \( O \) to the lines \( L_1 \) and \( L_2 \), respectively. Notice that the quadrilateral \( OMNP \) is cyclic because the sum of opposite angles \( \angle OMP \) and \( \angle ONP \) is \( 180^\circ \).

This implies that if the angle \( \angle NMP = \theta \) is acute, then the angle \( \angle NOM = \pi - \theta \) is obtuse. This property is crucial in determining the relative position of the origin concerning the angle bisectors.

Next, we express the equations of the lines in vector form. The given equations \( a_1 x + b_1 y = -c_1 \) and \( a_2 x + b_2 y = -c_2 \) can be rewritten as dot products of vectors. Since \( c_1 < 0 \) and \( c_2 < 0 \), both equations have positive right-hand sides.

We rewrite the equations as:

\[ (a_1 \hat{i} + b_1 \hat{j}) \cdot (x \hat{i} + y \hat{j}) = -c_1 \]

\[ (a_2 \hat{i} + b_2 \hat{j}) \cdot (x \hat{i} + y \hat{j}) = -c_2 \]

Interpreting these in vector form, we see that the vector along \( \overrightarrow{OM} \) is \( a_1 \hat{i} + b_1 \hat{j} \), and the vector along \( \overrightarrow{ON} \) is \( a_2 \hat{i} + b_2 \hat{j} \).

To find the relationship between these vectors, we calculate \( \cos(\pi - \theta) \) using the dot product formula:

\[ \cos(\pi - \theta) = \frac{(a_1 \hat{i} + b_1 \hat{j}) \cdot (a_2 \hat{i} + b_2 \hat{j})}{\sqrt{a_1^2 + b_1^2} \sqrt{a_2^2 + b_2^2}} \]

Simplifying this expression, we get:

\[ \cos(\pi - \theta) = -\cos(\theta) = \frac{a_1 a_2 + b_1 b_2}{\sqrt{a_1^2 + b_1^2} \sqrt{a_2^2 + b_2^2}} \]

Given that \( \theta \) is an acute angle, it follows that \( \cos(\theta) > 0 \). Therefore, for \( \cos(\theta) \) to be positive:

\[ a_1 a_2 + b_1 b_2 < 0 \]

From this analysis, we can conclude:

• The origin lies in the acute region if \( a_1 a_2 + b_1 b_2 < 0 \).
• Conversely, the origin lies in the obtuse region if \( a_1 a_2 + b_1 b_2 > 0 \).

This geometric and algebraic approach provides a clear method to determine the region in which the origin lies relative to the angle bisectors of the given lines.

Determining Whether the Origin Lies in the Acute or Obtuse Region

Surprisingly, we can use the theory of location of origin to distinguish angle bisector equations.

Given two lines:

\[ L_1: a_1 x + b_1 y + c_1 = 0 \]

\[ L_2: a_2 x + b_2 y + c_2 = 0 \]

The angle bisectors of these lines are given by:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

We will decide whether the positive sign gives the acute angle bisector or the negative sign does.

Let \( B_1 \) be the acute angle bisector, and let the origin \( O \) be in the acute region. Consider any point \( P(x, y) \) on the bisector \( B_1 \). Since \( O \) and \( P \) are in the same region, they must lie on the same sides of both lines \( L_1 \) and \( L_2 \).

If \( O \) and \( P \) are on the same side of \( L_1 \):

\[ (a_1 x + b_1 y + c_1) \times c_1 > 0 \implies a_1 x + b_1 y + c_1 < 0 \quad \text{(since \( c_1 < 0 \))} \]

Similarly, if \( O \) and \( P \) are on the same side of \( L_2 \):

\[ (a_2 x + b_2 y + c_2) \times c_2 > 0 \implies a_2 x + b_2 y + c_2 < 0 \quad \text{(since \( c_2 < 0 \))} \]

If \( P \) is in the other acute region, then \( O \) and \( P \) would be on opposite sides of \( L_1 \) and \( L_2 \). However, the same conclusions are reached, that if \( O \) and \( P \) are in the acute region, then:

\[ a_1 x + b_1 y + c_1 < 0 \]

\[ a_2 x + b_2 y + c_2 < 0 \]

Observe the bisector equation again:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

Since \( P(x, y) \) lies on the bisector \( B_1 \), and we have:

\[ a_1 x + b_1 y + c_1 < 0 \quad \text{and} \quad a_2 x + b_2 y + c_2 < 0 \]

We can only take the positive sign and reject the negative sign because a number cannot equal a negative number.

Thus, we conclude that if \( a_1 a_2 + b_1 b_2 < 0 \) (origin is in the acute region), then the positive sign gives the acute angle bisector, and the negative sign gives the obtuse angle bisector.

Similarly, if \( a_1 a_2 + b_1 b_2 > 0 \), then the positive sign gives the obtuse angle bisector, and the negative sign gives the acute angle bisector.

Conclusion

Given the lines:

\[ L_1: a_1 x + b_1 y + c_1 = 0 \]

\[ L_2: a_2 x + b_2 y + c_2 = 0 \]

where \( c_1 < 0 \) and \( c_2 < 0 \).

The angle bisectors of these lines are given by:

\[ \frac{a_1 x + b_1 y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2 x + b_2 y + c_2}{\sqrt{a_2^2 + b_2^2}} \]

If \( a_1 a_2 + b_1 b_2 < 0 \), the positive sign corresponds to the acute angle bisector, and the negative sign corresponds to the obtuse angle bisector. Conversely, if \( a_1 a_2 + b_1 b_2 > 0 \), the positive sign corresponds to the obtuse angle bisector, and the negative sign corresponds to the acute angle bisector.

Note: This method is not applicable if the origin lies on one of the lines or if the lines intersect at right angles (in which case the concepts of acute and obtuse regions are not defined).

Angle Bisectors of a Triangle

When the coordinates of the vertices of a triangle are known, calculating the angle bisectors becomes a straightforward task.

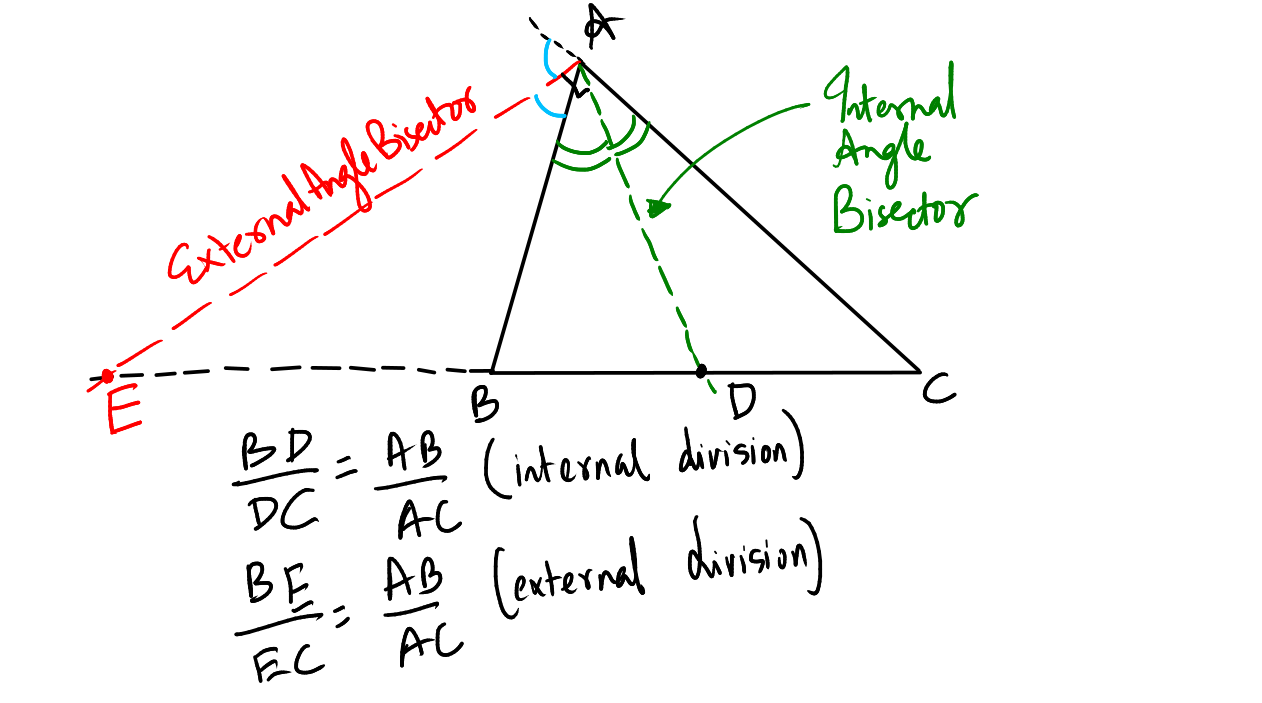
Consider a triangle \( \Delta ABC \) with known vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \). Using the angle bisector theorem, we can find points \( D \) and \( E \), where the internal angle bisector of \( \angle A \) intersects the opposite side \( BC \) at \( D \), and the external angle bisector of \( \angle A \) intersects \( BC \) at \( E \).

By the angle bisector theorem, we know:

\[ AD \text{ divides } BC \text{ internally in the ratio } \frac{AB}{AC} \]

\[ AE \text{ divides } BC \text{ externally in the ratio } \frac{AB}{AC} \]

To find the coordinates of points \( D \) and \( E \), we use the section formula. For point \( D \), which divides \( BC \) internally, the coordinates can be calculated as:

\[ D\left( \frac{x_2 \cdot AC + x_3 \cdot AB}{AB + AC}, \frac{y_2 \cdot AC + y_3 \cdot AB}{AB + AC} \right) \]

For point \( E \), which divides \( BC \) externally, the coordinates are:

\[ E\left( \frac{x_2 \cdot AC - x_3 \cdot AB}{AC - AB}, \frac{y_2 \cdot AC - y_3 \cdot AB}{AC - AB} \right) \]

Thus, using these coordinates, we can find the equations of the internal angle bisector \( AD \) and the external angle bisector \( AE \).

Note

• Internal Angle Bisector: The internal angle bisector of an angle in a triangle is the line segment that divides the angle into two equal parts. It extends from the vertex of the angle to the opposite side, intersecting it at a point that divides the side in the ratio of the other two sides.

• External Angle Bisector: The external angle bisector is the line that divides the external angle (formed by extending one of the sides of the triangle) into two equal parts. It intersects the extension of the opposite side of the triangle at a point that divides this extended side externally in the ratio of the other two sides.

Example

Consider a triangle \( \Delta ABC \) with vertices \( A(1, 5) \), \( B(-3, 2) \), and \( C(1, -3) \). Find the equation of the internal angle bisector of \( \angle A \).

Solution:

First, we calculate the lengths of sides \( AB \) and \( AC \).

\[ AB = \sqrt{(1 + 3)^2 + (5 - 2)^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = 5 \]

\[ AC = \sqrt{(1 - 1)^2 + (5 + 3)^2} = \sqrt{0 + 8^2} = \sqrt{64} = 8 \]

The internal angle bisector of \( \angle A \) intersects \( BC \) at \( D \) such that:

\[ \frac{BD}{DC} = \frac{AB}{AC} = \frac{5}{8} \]

Using the section formula, we find the coordinates of \( D \):

\[ D = \frac{5C + 8B}{5 + 8} = \frac{5(1, -3) + 8(-3, 2)}{13} = \frac{(5 - 24, -15 + 16)}{13} = \left( \frac{-19}{13}, \frac{1}{13} \right) \]

Now, we determine the equation of the line \( AD \). Using the two-point form of the line equation with points \( A(1, 5) \) and \( D \left( \frac{-19}{13}, \frac{1}{13} \right) \):

\[ \frac{y - 5}{x - 1} = \frac{\frac{1}{13} - 5}{\frac{-19}{13} - 1} = \frac{\frac{1 - 65}{13}}{\frac{-19 - 13}{13}} = \frac{\frac{-64}{13}}{\frac{-32}{13}} = 2 \]

Thus,

\[ \frac{y - 5}{x - 1} = 2 \implies y - 5 = 2(x - 1) \implies y - 5 = 2x - 2 \implies y = 2x + 3 \]

Therefore, the equation of the internal angle bisector \( AD \) is:

\[ y = 2x + 3 \]

Reflection

Finding the Equation of the Reflected Ray in the Cartesian Coordinate System

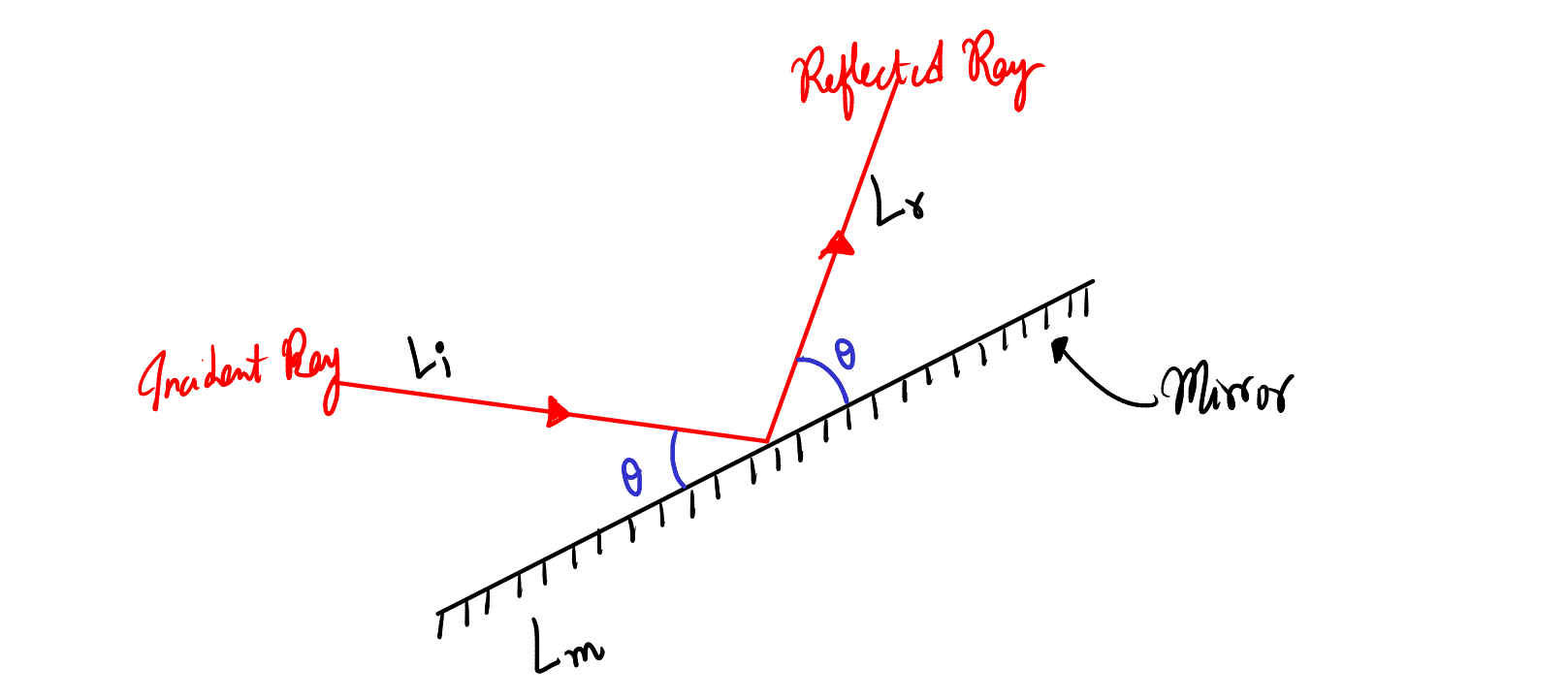
In the Cartesian coordinate system, when a ray of light strikes a mirror and gets reflected, the equation of the reflected ray can be determined using the laws of reflection and some basic geometric principles. Here, we outline the process to find the equation of the reflected ray given the equations of the mirror and the incident ray.

Steps to Find the Equation of the Reflected Ray

1. Identify the Mirror and the Incident Ray:

   Suppose the equation of the mirror is given by:

   \[ L_m: a_m x + b_m y + c_m = 0 \]

   and the equation of the incident ray is:

   \[ L_i: a_i x + b_i y + c_i = 0 \]

2. Find the Point of Incidence:

   The point of incidence is where the incident ray intersects the mirror. This can be found by solving the system of linear equations:

   \[ \begin{cases} a_m x + b_m y + c_m = 0 \\ a_i x + b_i y + c_i = 0 \end{cases} \]

   Solving these simultaneous equations will yield the coordinates \((x_0, y_0)\) of the point of incidence.

3. Determine the Slopes: Calculate the slopes of the mirror and the incident ray:

   • Slope of the mirror, \(m_m\):

     \[ m_m = -\frac{a_m}{b_m} \]

   • Slope of the incident ray, \(m_i\):

     \[ m_i = -\frac{a_i}{b_i} \]

4. Use the Law of Reflection:

   According to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, the angle between the incident ray and the mirror is equal to the angle between the mirror and the reflected ray. Using the tangent of the angles formed between the lines, we can express this relationship as:

   \[ \left| \frac{m_i - m_m}{1 + m_i m_m} \right| = \left| \frac{m_r - m_m}{1 + m_r m_m} \right| \]

   where \(m_r\) is the slope of the reflected ray.

5. Solve for the Slope of the Reflected Ray:

   Rearrange the equation to solve for \(m_r\):

   \[ \left| \frac{m_r - m_m}{1 + m_r m_m} \right| = \left| \frac{m_i - m_m}{1 + m_i m_m} \right| \]

   This implies two possible solutions for \(m_r\), corresponding to the positive and negative cases of the absolute value. Select the appropriate \(m_r\) that satisfies the geometric configuration.

6. Form the Equation of the Reflected Ray:

   Once \(m_r\) is determined, use the point-slope form to write the equation of the reflected ray passing through the point of incidence \((x_0, y_0)\):

   \[ y - y_0 = m_r (x - x_0) \]

By following these steps, you can find the equation of the reflected ray in the Cartesian coordinate system.

Example

Finding the Equation of the Reflected Ray

Consider the mirror with the equation:

\[ L_m: 2x + y - 3 = 0 \]

and the incident ray with the equation:

\[ L_i: 3x - y - 2 = 0 \]

We will find the equation of the reflected ray.

Step 1: Find the Point of Incidence

To find the point of incidence, solve the system of equations:

\[ \begin{cases} 2x + y - 3 = 0 \\ 3x - y - 2 = 0 \end{cases} \]

Adding the two equations to eliminate \(y\):

\[ (2x + y - 3) + (3x - y - 2) = 0 \implies 5x - 5 = 0 \implies x = 1 \]

Substitute \( x = 1 \) into \( 2x + y - 3 = 0 \):

\[ 2(1) + y - 3 = 0 \implies 2 + y - 3 = 0 \implies y = 1 \]

Thus, the point of incidence is \((1, 1)\).

Step 2: Determine the Slopes

• Slope of the mirror \( L_m \):

\[ m_m = -\frac{a_m}{b_m} = -\frac{2}{1} = -2 \]

• Slope of the incident ray \( L_i \):

\[ m_i = -\frac{a_i}{b_i} = -\frac{3}{-1} = 3 \]

Step 3: Use the Law of Reflection

Using the tangent of the angles formed between the lines, we can express this relationship as:

\[ \left| \frac{m_i - m_m}{1 + m_i m_m} \right| = \left| \frac{m_r - m_m}{1 + m_r m_m} \right| \]

Substituting the known slopes:

\[ \left| \frac{3 - (-2)}{1 + 3(-2)} \right| = \left| \frac{m_r - (-2)}{1 + m_r(-2)} \right| \]

\[ \left| \frac{5}{1 - 6} \right| = \left| \frac{m_r + 2}{1 - 2m_r} \right| \]

\[ \left| \frac{5}{-5} \right| = \left| \frac{m_r + 2}{1 - 2m_r} \right| \]

\[ 1 = \left| \frac{m_r + 2}{1 - 2m_r} \right| \]

This implies:

\[ 1 = \frac{m_r + 2}{1 - 2m_r} \quad \text{or} \quad 1 = \frac{-(m_r + 2)}{1 - 2m_r} \]

For the first case:

\[ 1 = \frac{m_r + 2}{1 - 2m_r} \implies 1 - 2m_r = m_r + 2 \implies 1 - 2m_r - m_r = 2 \implies 1 - 3m_r = 2 \implies -3m_r = 1 \implies m_r = -\frac{1}{3} \]

For the second case:

\[ 1 = \frac{-(m_r + 2)}{1 - 2m_r} \implies 1 - 2m_r = -(m_r + 2) \implies 1 - 2m_r = -m_r - 2 \implies 1 - 2m_r + m_r = -2 \implies 1 - m_r = -2 \implies -m_r = -3 \implies m_r = 3 \]

Since the slope \( m_i \) is 3, the second case \( m_r = 3 \) corresponds to the incident ray slope and doesn't give us the reflected ray's slope. Therefore, the reflected ray slope \( m_r = -\frac{1}{3} \).

Step 4: Form the Equation of the Reflected Ray

Using the point-slope form for the point \((1, 1)\) and the slope \( m_r = -\frac{1}{3} \):

\[ y - 1 = -\frac{1}{3}(x - 1) \]

\[ y - 1 = -\frac{1}{3}x + \frac{1}{3} \]

\[ y = -\frac{1}{3}x + \frac{1}{3} + 1 \]

\[ y = -\frac{1}{3}x + \frac{4}{3} \]

Multiplying through by 3 to clear the fraction:

\[ 3y = -x + 4 \]

\[ x + 3y = 4 \]

Thus, the equation of the reflected ray is:

\[ x + 3y = 4 \]