Range of Quadratic Expressions

What is the range of an expression?

The range of a mathematical expression refers to the set of all possible output values generated by the expression, given the variety of inputs it can accept. You can think of it as the output spectrum of a machine when different inputs are fed into it.

Illustration with Examples:

Constant Expression:
- For a constant expression like \( y = 5 \), no matter what input you provide, the output will always be 5.
- The range of this expression is simply {5}.
Absolute Value Expression:
- Consider \( y = |x| \).
- Regardless of the input \( x \) (whether positive, negative, or zero), the output \( y \) is always non-negative.
- The range of this expression is all non-negative real numbers.
Exponential Expression:
- Take \( y = 2^x \).
- As \( x \) varies over all real numbers, \( y \) grows exponentially for positive \( x \) and approaches zero (but never reaches it) for negative \( x \).
- The range is all positive real numbers (0, ∞).
Reciprocal Expression:
- For \( y = \frac{1}{x} \),
- As \( x \) takes any non-zero real number, \( y \) becomes the reciprocal of \( x \). \( y \) can be very large or very small but never zero.
- The range is all real numbers except 0.

These examples showcase how the range is determined by observing how the output changes with varying inputs, reflecting the different behaviors of various mathematical expressions.

Domain is all possible real numbers

Given that input \(x\) is allowed to vary for all possible real numbers, to determine the range of a quadratic expression \( ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are real numbers, we intuitively infer the range from the graph. We follow the following process:

Calculate the Discriminant:
- Compute the discriminant \( \Delta = b^2 - 4ac \).
Find the Vertex:
- The vertex of the quadratic expression is given by \( \left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \).
Determine the Direction of Opening:
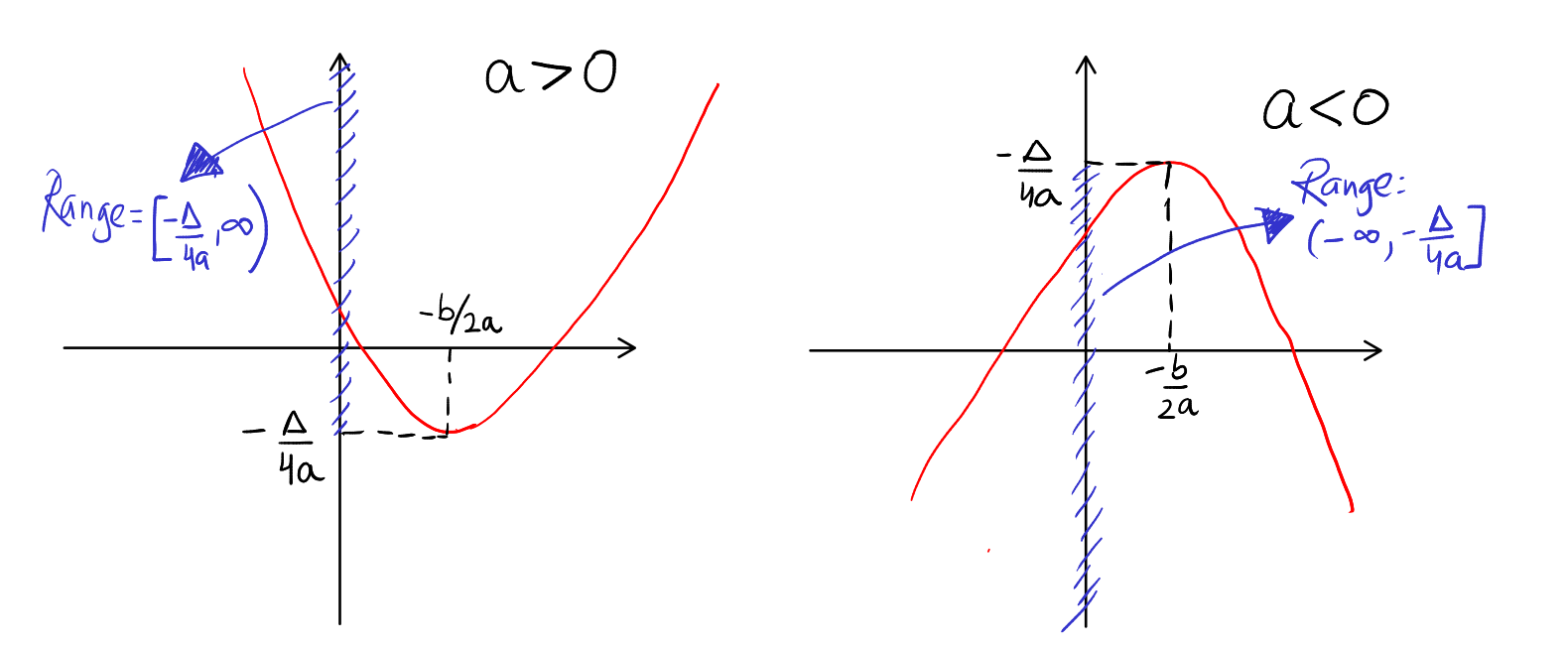
- If \( a > 0 \), the parabola opens upwards.
- If \( a < 0 \), it opens downwards.
Calculate the Range:
- Upward Opening Parabola (\( a > 0 \)):
  - The minimum value of the function is at the vertex. The y-coordinate of the vertex, \( -\frac{\Delta}{4a} \), gives the minimum value.
  - The range is \( y \geq -\frac{\Delta}{4a} \).
- Downward Opening Parabola (\( a < 0 \)):
  - The maximum value of the function is at the vertex. The y-coordinate of the vertex, \( -\frac{\Delta}{4a} \), provides the maximum value.
  - The range is \( y \leq -\frac{\Delta}{4a} \).

Using these steps, the range of any quadratic expression \( ax^2 + bx + c \) can be determined based on the direction of its parabola and the y-coordinate of its vertex.

Domain is restricted

When the domain is not allowed to vary over all possible real numbers, it may affect the range.

Let's cover all possible cases when determining the range of the quadratic expression \( ax^2 + bx + c \) over a restricted interval \([m, n]\):

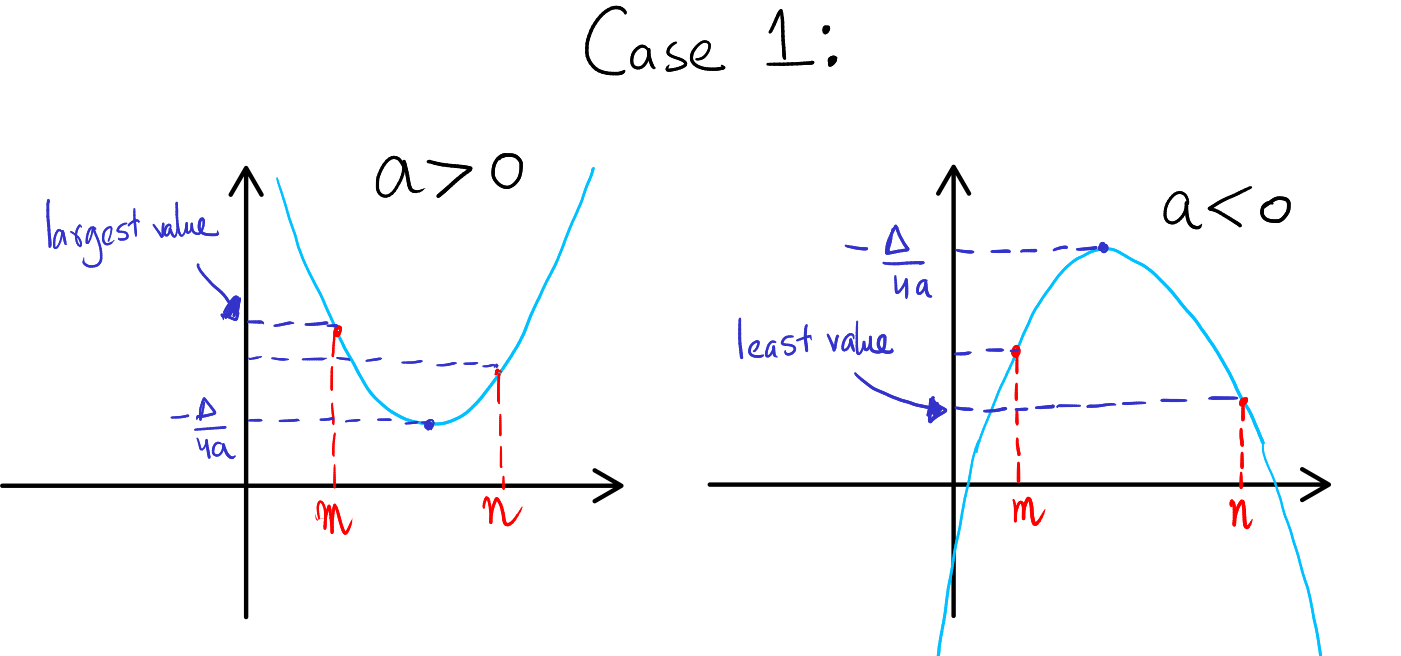
Case 1: Vertex Inside the Interval ([m, n]):
- If \( a > 0 \) (Upward-Opening Parabola): The minimum value occurs at the vertex if the vertex's x-coordinate is within \([m, n]\). The maximum value will be at one of the interval's endpoints (either \( m \) or \( n \), whichever gives the larger y-value).
- If \( a < 0 \) (Downward-Opening Parabola): The maximum value occurs at the vertex if the vertex's x-coordinate is within \([m, n]\). The minimum value will be at one of the interval's endpoints (either \( m \) or \( n \), whichever gives the smaller y-value).
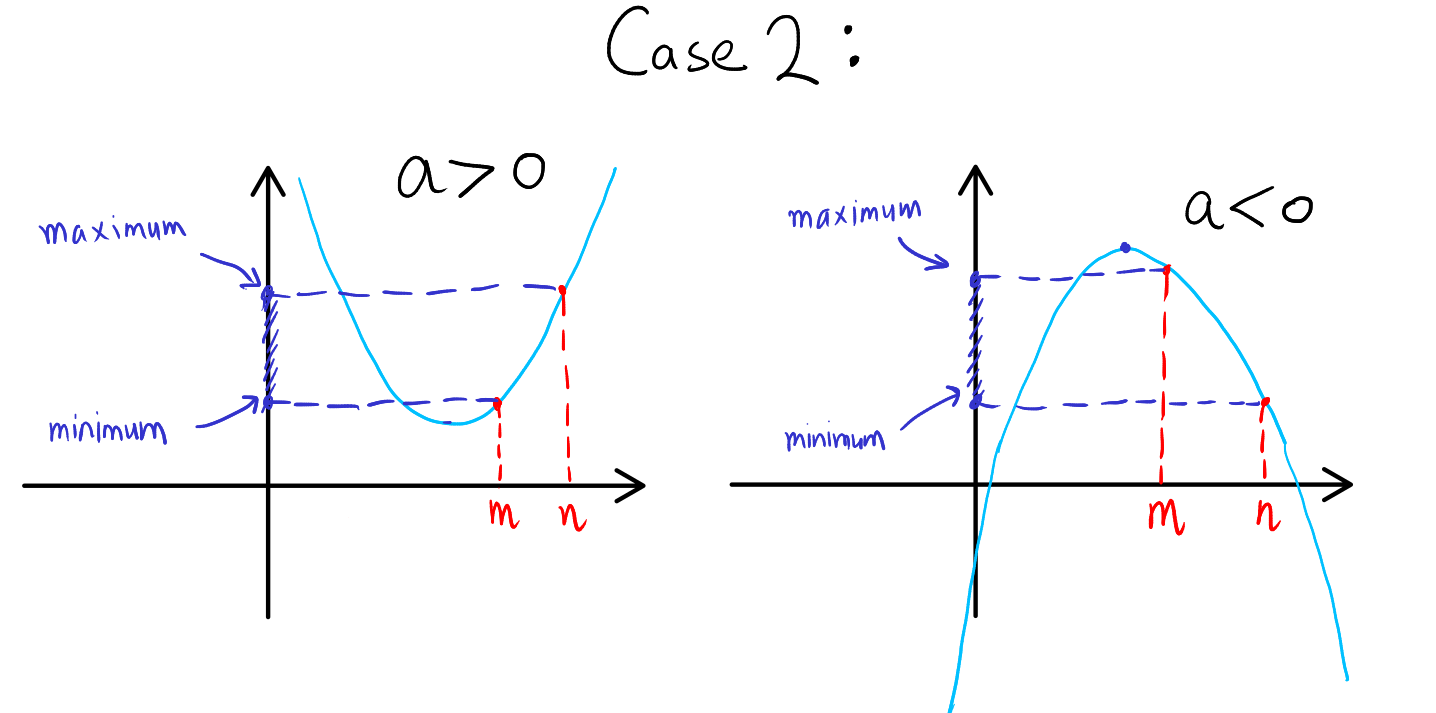
Case 2: Vertex Outside the Interval ([m, n]):
- If \( a > 0 \): The range will be between the y-values at the endpoints \(m\) and \(n\).
- If \( a < 0 \): Similarly, the range will be between the y-values at the endpoints \(m\) and \(n\).
Case 3: Vertex at an Endpoint of the Interval:
- If \( a > 0 \) and the vertex is at \( m \) or \( n \): The range starts from the y-value of the vertex and extends to the y-value at the other endpoint.
- If \( a < 0 \) and the vertex is at \( m \) or \( n \): The range starts from the y-value at the non-vertex endpoint and extends to the y-value of the vertex.

By carefully considering these cases, you can accurately determine the range of the quadratic expression over any given interval. The direction in which the parabola opens (determined by the sign of \( a \)) and the position of the vertex relative to the interval are key factors in this analysis. It should be clearer after considering the following examples:

Example for Case 1: Vertex Inside the Interval Quadratic Expression: \( y = x^2 - 4x - 3 \) Interval: \([-1, 3]\)

Find the Vertex:
- Vertex formula: \( x = -\frac{b}{2a} \). Here, \( a = 1, b = -4 \).
- Vertex: \( x = -\frac{-4}{2 \cdot 1} = 2 \).
- Y-coordinate of the vertex: \( y = 2^2 - 4 \cdot 2 - 3 = -3 \).
- Vertex is at \( (2, -3) \), within the interval \([-1, 3]\).
Evaluate at Interval Endpoints:
- At \( x = -1 \): \( y = (-1)^2 - 4 \cdot (-1) - 3 = 2 \).
- At \( x = 3 \): \( y = 3^2 - 4 \cdot 3 - 3 = 0 \).
Determine the Range:
- With the vertex inside the interval and the parabola opening upwards, the range is from \( -3 \) to \( 2 \).
- Range: \([-3, 2]\).

Example for Case 2: Vertex Outside the Interval Quadratic Expression: \( y = x^2 + 6x - 1 \) Interval: \([-2, 1]\)

Find the Vertex:
- For \( a = 1, b = 6 \), the vertex is at \( x = -3 \) with y-coordinate \( y = -10 \).
- Vertex: \( (-3, -10) \), outside the interval \([-2, 1]\).
Evaluate at Interval Endpoints:
- At \( x = -2 \): \( y = -9 \).
- At \( x = 1 \): \( y = 6 \).
Determine the Range:
- With the vertex outside and the parabola opening upwards, the range is determined by the endpoint values.
- Range: \([-9, 6]\).

When you just want the range

If the specific locations of the minimum and maximum values are not of concern, and you simply want to find the range of the quadratic expression \( ax^2 + bx + c \) over a given interval \([m, n]\), you can follow a more direct approach:

Calculate \(-\frac{\Delta}{4a}\):
- Compute the value of \(-\frac{\Delta}{4a}\), where \( \Delta = b^2 - 4ac \). This gives you the y-coordinate of the vertex of the parabola.
Evaluate the Expression at the Interval Endpoints:
- Calculate the values of the quadratic expression at the endpoints of the interval: \( y(m) = am^2 + bm + c \) and \( y(n) = an^2 + bn + c \).
Determine the Range:
- The range of the quadratic expression over the interval \([m, n]\) will be the minimum and maximum values among \(-\frac{\Delta}{4a}\), \( y(m) \), and \( y(n) \).
- Formally, the range is given by \([\min(-\frac{\Delta}{4a}, y(m), y(n)), \max(-\frac{\Delta}{4a}, y(m), y(n))]\).

This method simplifies the process by focusing on the key values that influence the range of the quadratic expression over the specified interval. It's a practical approach when only the range is required without needing the exact points where the maximum and minimum occur.

Another example:
Find the range of \( \sin^2(x) - 3\sin(x) + 4 \), \(x\in\mathbb R\).
Solution:
To find the range of the expression \( \sin^2(x) - 3\sin(x) + 4 \), follow these steps:

Substitute with a New Variable:
- Let \( t = \sin(x) \). The expression becomes a quadratic in \( t \): \( t^2 - 3t + 4 \).
- The range of \( t \) (since \( t = \sin(x) \)) is \([-1, 1]\).
Use Discriminant to Find Vertex:
- For a quadratic expression \( at^2 + bt + c \), the vertex's y-coordinate is given by \( -\frac{\Delta}{4a} \) where \( \Delta = b^2 - 4ac \).
- Here, \( a = 1, b = -3, c = 4 \), so \( \Delta = (-3)^2 - 4 \times 1 \times 4 = 9 - 16 = -7 \).
- The y-coordinate of the vertex is \( -\frac{-7}{4 \times 1} = \frac{7}{4} \).
Evaluate at the Endpoints of t's Range:
- For \( t = -1 \): \( (-1)^2 - 3(-1) + 4 = 1 + 3 + 4 = 8 \).
- For \( t = 1 \): \( 1^2 - 3 \times 1 + 4 = 1 - 3 + 4 = 2 \).
Determine the Range:
- Since the vertex's y-coordinate is outside the possible y-values for the given range of \( t \) (\([-1, 1]\)), it does not impact the range of the original expression.
- The range of the expression will be the minimum and maximum values obtained from evaluating at \( t = -1 \) and \( t = 1 \).
- Therefore, the range of \( \sin^2(x) - 3\sin(x) + 4 \) is from 2 to 8.

This method simplifies the process of finding the range by substituting \( \sin(x) \) with \( t \), evaluating the quadratic at the endpoints of \( t \)'s range, and utilizing the discriminant to confirm the vertex's y-coordinate.