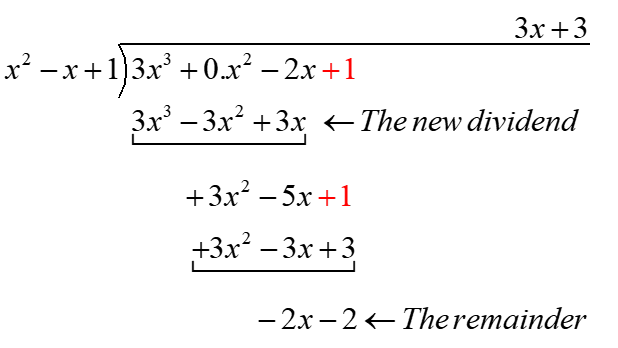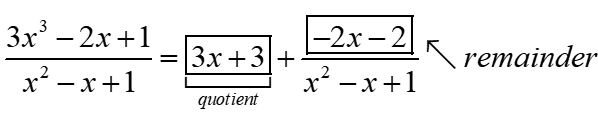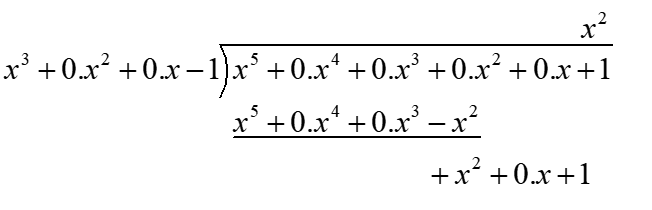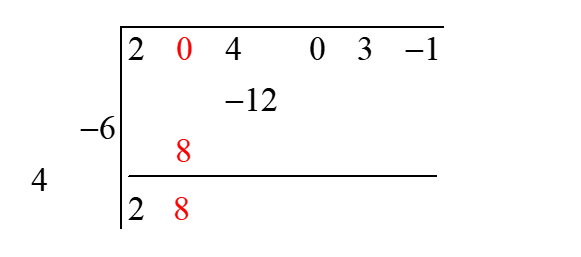Introduction
The study of polynomial equations is one of the oldest mathematical endeavors, predating even the discovery of negative numbers. Historically, solutions to quadratic equations were identified early on, leading to the development of a general formula that is well-known today. However, finding the roots of cubic equations proved more challenging; it took mathematicians centuries to devise a corresponding formula.
The quest continued for a formula to solve higher degree polynomials. Eventually, it culminated with the astonishing discovery by Niels Henrik Abel that no general formula using radicals exists for polynomial equations of degree greater than four. This revelation laid the groundwork for the field of Abstract Algebra, an essential area of higher mathematics.
This discussion aims to provide a clear understanding of polynomials, including their properties and the methods for determining the number of roots. We will begin with foundational concepts and incrementally progress to more complex theories and problem-solving techniques.
Now, let's define a polynomial.
The word "Polynomial" originates from the Greek "poly," meaning 'many,' and "nomial," referring to 'terms.' In mathematics, a polynomial is an expression comprising a finite number of terms. Each term is formed from the product of a coefficient and a variable raised to a non-negative integer exponent. The degree of each term is the exponent of the variable, and the degree of the polynomial is the highest degree of any term within the expression.
Take, for instance, the polynomial \( 2xy - 3x^2 \). This expression consists of two terms and involves two independent variables, \( x \) and \( y \). The first term includes the coefficient 2 and is associated with both variables \( x \) and \( y \), each to the first power, giving the term a total degree of 1 + 1 = 2. The second term has the coefficient -3 and is solely dependent on the variable \( x \), which is squared, hence this term has a degree of 2.
Consider another polynomial: \( -3x^3 + 2xy + 4x - 2 \). This one contains four terms with the variables \( x \) and \( y \). Analyzing each term: the first has a coefficient of -3 with \( x \) raised to the third power, resulting in a degree of 3. The second term, \( 2xy \), has a coefficient of 2 and a total degree of 2, resulting from \( x \) and \( y \) each being to the first power. The third term is \( 4x \), with a coefficient of 4 and a degree of 1. The final term is a constant -2, with a coefficient of -2 and a degree of 0. The polynomial's degree is determined by the term with the highest degree, which in this case is 3.
Thus, it's clear that even a single constant term qualifies as a polynomial, specifically of degree 0, due to its lack of variables.
It is crucial to note that variable exponents in a polynomial must be non-negative integers. This is why the expression \( 2x^2 - \frac{1}{x} \) is not considered a polynomial, as the second term involves \( x \) to the negative first power.
Furthermore, polynomials are characterized by a finite number of terms. An expression with an infinite number of terms, such as a power series, is distinct from a polynomial and possesses its own set of properties and applications.
Consider the series \( \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots + \frac{x^n}{n!} + \frac{x^{n+1}}{(n+1)!} + \ldots \), which is a power series, not a polynomial, because it contains an infinite number of terms.
Polynomials can have coefficients that are either real numbers or complex numbers. For those not familiar with complex numbers, there's no need for concern; they will be covered in later chapters. This text will focus on polynomials with real coefficients, also known as real polynomials.
A real polynomial in one variable is a polynomial with real coefficients that depends on a single variable. These are also termed univariate polynomials. An example of such a polynomial is \( P(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \ldots + a_{n-1}x + a_n \), where each coefficient \( a_0, a_1, \ldots, a_n \) is real, and the degree of the polynomial is a non-negative integer \( n \). Polynomials are often represented using function notation, such as \( P \) for a polynomial dependent on variable \( x \). It's common to use capital letters to denote polynomials, although this is not a hard and fast rule. Importantly, the leading coefficient \( a_0 \) is non-zero; otherwise, the polynomial's degree would be less than \( n \).
The term \( a_0x^n \) is the leading term, and \( a_0 \) is the leading coefficient. Their significance will be elaborated on in subsequent sections.
Examples of real polynomials in one variable include:
\( P(x) = 2 \), \( P(x) = -3x + 1 \), \( P(x) = 2x^2 - 3x + 1 \), \( Q(x) = 5x^4 + 2x - 1 \).
Polynomials of degree zero are simply constant polynomials. Polynomials of degree one are called linear, degree two are quadratic, degree three are cubic, degree four are quartic or biquadratic, and degree five are quintic. Polynomials of higher degrees have specific names based on their degree, such as sextic for degree six and septic or heptic for degree seven.
Real Polynomials of one variable:
A polynomial that features real coefficients and is a function of a single variable is known as a real polynomial of one variable, also referred to as a univariate polynomial.
Such a polynomial is generally expressed as \( P(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + ... + a_{n-1}x + a_n \), where each of the coefficients \( a_0, a_1, ..., a_n \) is real, and the degree of the polynomial is a non-negative integer \( n \). This function is dependent on the variable \( x \), and it is customary (though not obligatory) to use capital letters for the names of polynomials, such as \( P \) in this case. The leading coefficient \( a_0 \) must be non-zero; otherwise, the polynomial would have a degree less than \( n \).
The term with the highest degree in the polynomial is \( a_0x^n \) and is called the leading term, while \( a_0 \) is known as the leading coefficient. The significance of the leading term will be covered in more detail later.
Examples of real polynomials of one variable are:
\( P(x) = 2 \), \( P(x) = -3x + 1 \), \( P(x) = 2x^2 - 3x + 1 \), \( Q(x) = 5x^4 + 2x - 1 \).
Polynomials are categorized based on their degree:
- Polynomials of degree zero are constant polynomials.
- Degree one polynomials are termed linear polynomials.
- Degree two polynomials are known as quadratic polynomials.
- Degree three are cubic polynomials.
- Degree four are referred to as quartic or biquadratic polynomials.
- Degree five polynomials are identified as quintic.
- The naming continues for higher degrees, such as sextic for degree six, and so on.
For convenience, the symbol \( \delta \) will be used to represent the degree of a polynomial. For example, if \( P(x) = 3x^3 + 2x^2 - 5x - 1 \), then \( \delta(P) = 3 \) indicating that the degree of \( P \) is 3.
From now onwards, the term 'Polynomial' will be used instead of the longer 'Real polynomials of one variable'.
Monic Polynomial
A monic polynomial is a type of univariate polynomial characterized by having the leading coefficient equal to 1. This leading term, therefore, is simply the highest degree term of the variable without any multiplicative constant other than 1. For example, the polynomial \( q(x) = x^2 + 4x - 1 \) is a monic polynomial because the coefficient of the highest power of \( x \) is 1.
Every polynomial \( p(x) \) of degree \( n \geq 1 \) can be represented in the form \( p(x) = a_0q(x) \), where \( a_0 \) is the leading coefficient of \( p(x) \), and \( q(x) \) is a monic polynomial of the same degree \( n \). Essentially, \( q(x) \) is obtained by dividing \( p(x) \) by its leading coefficient \( a_0 \).
For example, consider a polynomial \( p(x) \) of degree 3, say \( p(x) = 2x^3 - 6x^2 + 8x - 4 \). Here, the leading coefficient \( a_0 \) is 2. To express \( p(x) \) as a product of its leading coefficient and a monic polynomial, we divide each term by 2:
Now, \( q(x) = x^3 - 3x^2 + 4x - 2 \) is the monic polynomial of degree 3, as its leading term \( x^3 \) has a coefficient of 1.
Evaluating a Polynomial
In the algebra of polynomials, evaluating a polynomial at a certain value of \( x \) is a fundamental operation. For example, for the polynomial \( P(x) = 3x^3 + 2x^2 - 4x + 2 \), to find the value at \( x = -1 \), we substitute \( -1 \) into the polynomial, yielding \( P(-1) = 3(-1)^3 + 2(-1)^2 - 4(-1) + 2 = -3 + 2 + 4 + 2 = 5 \).
A polynomial \( P(x) \) is generally defined as \( P(x) = a_0x^n + a_1x^{n-1} + ... + a_n \), where \( a_0, a_1, ..., a_n \) are coefficients. Evaluating this polynomial at \( x = 0 \) yields \( P(0) = a_n \), which gives us the constant term of the polynomial. To obtain the sum of all coefficients of the polynomial, one can evaluate it at \( x = 1 \), which simplifies to \( P(1) = a_0 + a_1 + ... + a_n \).
Algebra of Polynomials
If we consider two polynomials, \( P(x) \) and \( Q(x) \), defined respectively as \( P(x) = a_0x^n + a_1x^{n-1} + ... + a_n \), and \( Q(x) = b_0x^m + b_1x^{m-1} + ... + b_m \), where \( \delta(P) \) is the degree of \( P \) which is \( n \), and \( \delta(Q) \) is the degree of \( Q \) which is \( m \), various operations such as addition, subtraction, multiplication, and division can be performed on these polynomials following algebraic rules.
Addition of Polynomials
The sum of two polynomials \( P(x) \) and \( Q(x) \) is defined as \( (P + Q)(x) = P(x) + Q(x) \), meaning that the value of \( P + Q \) at any point \( x \) is the sum of the values of \( P \) at \( x \) and \( Q \) at \( x \).
The degree of the resulting polynomial \( P + Q \) is determined by the higher degree of the two polynomials \( P \) and \( Q \):
However, if \( \delta(P) = \delta(Q) \), the resulting degree may be less than \( \delta(P) \) or \( \delta(Q) \) if the leading terms cancel each other out.
For example, consider the polynomials \( P(x) = x^3 + 2x^2 - x + 1 \) and \( Q(x) = -x^3 - 2x^2 + 6x - 2 \). The sum \( (P + Q)(x) \) simplifies to \( -7x + 3 \). Here, both \( P \) and \( Q \) have a degree of 3, but \( \delta(P + Q) \) is 1 because the terms containing \( x^3 \) and \( x^2 \) cancel each other out.
Multiplication of Polynomials
The product of two polynomials \( P(x) \) and \( Q(x) \) is denoted as \( PQ(x) = P(x)Q(x) \). This means that the value of \( PQ \) at any point \( x \) is the product of the values of \( P \) at \( x \) and \( Q \) at \( x \).
The degree of the product polynomial \( PQ \) is the sum of the degrees of \( P \) and \( Q \):
This property is straightforward to demonstrate.
For example, take \( P(x) = x^3 + 2x - 1 \) and \( Q(x) = 4x^2 + 2x - 1 \). The product \( PQ(x) \) is given by multiplying each term in \( P(x) \) by each term in \( Q(x) \), leading to:
The resulting polynomial after multiplying and combining like terms would be:
[ PQ(x) = 4x^5 + \ldots ] (with additional terms resulting from the multiplication process).
Here, \( \delta(P) = 3 \) and \( \delta(Q) = 2 \), so according to the rule, \( \delta(PQ) = 3 + 2 = 5 \), which aligns with the leading term \( 4x^5 \) in the expanded product.
Composition of Polynomials
The composition of two polynomials \( P \) and \( Q \) is denoted by \( P(Q(x)) \), which means that the polynomial \( Q(x) \) is substituted for every occurrence of \( x \) in polynomial \( P(x) \). In other words, \( P(Q(x)) = a_0(Q(x))^n + a_1(Q(x))^{n-1} + \ldots + a_n \), where the \( x \) in the expression of \( P(x) \) is completely replaced by \( Q(x) \).
To illustrate, let's take \( P(x) = 4x^2 - 2x + 3 \) and \( Q(x) = x^2 - x \). Then the composition \( P(Q(x)) \) is:
When computing this, you combine like terms to get the resulting polynomial.
The degree \( \delta \) of the composition \( P(Q(x)) \) is the product of the degrees of \( P \) and \( Q \):
For instance, if \( P \) and \( Q \) both have a degree of 2, then \( P(Q(x)) \) would have a degree of 4, assuming there's no cancellation of the highest degree terms.
If \( P(x) \) has the same degree as \( P(Q(x)) \), it implies that the degree of \( Q(x) \) must be 1, which means \( Q(x) \) is a linear polynomial. This is because the composition of a polynomial with a linear polynomial does not change the degree of the original polynomial.
Rational Expression
A rational expression is a fraction in which both the numerator and the denominator are polynomials. The numerator represents the dividend, and the denominator represents the divisor. The degree of the polynomial in the numerator can be less than, equal to, or greater than the degree of the polynomial in the denominator. Rational expressions are analogous to rational numbers, where the numerator and denominator are integers.
Here are four examples of rational expressions:
-
\( \frac{x^2 - 4}{x - 2} \)
-
\( \frac{3x^3 + 2x - 7}{x^2 + x + 1} \)
-
\( \frac{5x - 1}{3x^2 - x + 4} \)
-
\( \frac{x^4 - 2x^2 + x - 6}{x^3 - 3x + 2} \)
Proper and Improper Rational Expressions
A rational expression is classified as proper if the degree of the numerator polynomial is less than the degree of the denominator polynomial. Conversely, it is termed improper if the degree of the numerator is equal to or greater than the degree of the denominator.
Examples of each include:
Proper rational expression:
(The degree of the numerator is 1, and the degree of the denominator is 2.)
Improper rational expression:
(The degree of the numerator is 3, and the degree of the denominator is 2.)
Euclidian Division of Polynomials
Before we understand what the algorithm is, let us try to solve the following problem:
Problem:
Given two polynomials, \( p(x) = x^3 + 2x^2 - 3x + 1 \) and \( d(x) = x^2 + x - 1 \), find polynomials \( q(x) \) and \( r(x) \) such that \( p(x) \) can be expressed in the form \( p(x) = q(x)d(x) + r(x) \), where the degree of \( r(x) \) is less than the degree of \( d(x) \). The polynomial \( q(x) \) will be the quotient resulting from the division of \( p(x) \) by \( d(x) \), and \( r(x) \) will be the remainder of this division. The goal is to determine \( q(x) \) and \( r(x) \) such that the degree of \( r(x) \) is minimized.
Solution:
Given the polynomials:
- \( p(x) = x^3 + 2x^2 - 3x + 1 \)
- \( d(x) = x^2 + x - 1 \)
We aim to find \( q(x) \) and \( r(x) \) such that \( p(x) = q(x)d(x) + r(x) \).
Step 1: Matching the Highest Degree Term
We choose \( q(x) = x \) because multiplying \( d(x) \) by \( x \) gives us \( x^3 \), which matches the highest degree term of \( p(x) \).
So we start with:
Step 2: Calculating the Initial Remainder \( r(x) \)
Multiplying out and subtracting from \( p(x) \), we get:
Step 3: Further Division of the Remainder
We see that the remainder \( r(x) \) is still divisible by \( d(x) \), so we perform another division:
Multiplying out and finding the new remainder, we have:
Step 4: Final Expression
Finally, we compile our results into the original polynomial \( p(x) \):
So we have found the quotient \( q(x) = x + 1 \) and the remainder \( r'(x) = -3x + 2 \) of minimum degree that satisfy \(p(x)=q(x)d(x)+r(x)\). You should verify whether both sides are equal or not.
In the context of polynomial division, the expression \( p(x) = q(x)d(x) + r(x) \) can be reformulated as \( \frac{p(x)}{d(x)} = q(x) + \frac{r(x)}{d(x)} \). This formulation closely parallels the division of integers. For example, dividing 13 by 3 in integer arithmetic yields 4 with a remainder of 1, which can be represented as \( \frac{13}{3} = 4 + \frac{1}{3} \). In this analogy:
- 4 represents the quotient, which is the integer part of the division.
- \( \frac{1}{3} \) represents the remainder over the divisor, indicating what's left after the division.
Translating this concept to polynomial division:
- \( p(x) \) is the dividend, the polynomial being divided.
- \( d(x) \) is the divisor, the polynomial by which \( p(x) \) is divided.
- \( q(x) \) is the quotient polynomial, analogous to the integer quotient in numerical division. It represents how many times \( d(x) \) can be "contained" within \( p(x) \).
- \( r(x) \) is the remainder polynomial, similar to the numerical remainder. It's what remains from \( p(x) \) after subtracting the product of \( q(x) \) and \( d(x) \).
This division demonstrates that any polynomial \( p(x) \) divided by a non-zero polynomial \( d(x) \) can be expressed as a sum of a quotient polynomial \( q(x) \) and a fraction \( \frac{r(x)}{d(x)} \), where \( r(x) \) is a polynomial of lesser degree than \( d(x) \). If \( r(x) = 0 \), then \( p(x) \) is exactly divisible by \( d(x) \), and \( p(x)/d(x) = q(x) \).
This division process is foundational in understanding how polynomials can be broken down, analyzed, and simplified, providing insights into the structure of polynomial expressions and facilitating operations like factorization, finding roots, and simplifying complex rational expressions.
The Euclidean Division of Polynomials is an algorithmic process akin to the familiar division of integers. It states that for any two polynomials \( p(x) \) and \( d(x) \), where \( d(x) \) is not the zero polynomial and its degree is less than or equal to the degree of \( p(x) \), there exist unique polynomials \( q(x) \) and \( r(x) \) such that:
Here, \( q(x) \) is known as the quotient polynomial and \( r(x) \) as the remainder polynomial, with the degree of \( r(x) \) strictly less than the degree of \( d(x) \). This relationship can also be written as a rational expression:
This resembles the division of integers, where you divide a number to get a quotient and a remainder.
In the context of polynomials: - \( p(x) \) is referred to as the dividend. - \( d(x) \) is the divisor. - The outcome of the division \( q(x) \) is the quotient. - \( r(x) \) is the remainder.
The degree of the quotient polynomial \( q(x) \) is the difference between the degrees of \( p(x) \) and \( d(x) \). Specifically, if the degree of \( p(x) \) is \( p \) and the degree of \( d(x) \) is \( d \), then:
The division can be performed using long division, which is methodical and mirrors integer division, or synthetic division, which is a shortcut applicable when the divisor \( d(x) \) is a monic linear polynomial. The Euclidean Division algorithm is particularly useful for finding roots, factoring polynomials, and simplifying rational expressions.
Long Division of Polynomials
The long division of polynomials is a systematic method that mirrors the traditional long division of integers. Here's the step-by-step algorithm:
-
Arrange Polynomials: Start by writing both the dividend \( p(x) \) and the divisor \( d(x) \) in descending order of their degrees. If there's any missing term in the polynomial sequence, introduce that term with a zero coefficient to maintain order.
-
Divide Leading Terms: Take the leading term (the term with the highest power of \( x \)) of the dividend and divide it by the leading term of the divisor. This gives you the first term of the quotient.
-
Multiply and Subtract: Multiply the entire divisor by this first term of the quotient. Then, subtract this result from the dividend, which will give you a new polynomial, often referred to as the remainder.
-
New Dividend: This remainder becomes the new dividend. Now, take its leading term and divide it by the leading term of the original divisor to get the next term of the quotient.
-
Iterate the Process: Repeat the multiplication and subtraction steps with the new dividend and the divisor. Continue this process, each time appending the next term to the quotient, until you obtain a remainder with a degree that is less than the degree of the divisor.
-
Conclude with Remainder: The process stops when you can no longer divide because the remainder's degree is lower than the divisor's. This remainder is then written over the divisor to complete the expression of the result.
Let us understand with a few examples how it works.
Example
Problem: Divide the polynomial \(3{{x}^{3}}-2x+1\) by \({{x}^{2}}-x+1\) .
Solution:
Let the dividend be \(p(x)=3{{x}^{3}}+0{{x}^{2}}-2x+1\) (insert the missing term having coefficient 0)
Thus, we get,
Example
Problem: Find the remainder when \(x^5+1\) is divided by \(x^3-1\).
Solution:
Here's a breakdown of the steps:
-
Division: The first step is to divide \( x^5 \), the leading term of the dividend, by \( x^3 \), the leading term of the divisor, which gives us \( x^2 \) as the first term of the quotient.
-
Multiplication: Multiply the entire divisor \( x^3 - 1 \) by \( x^2 \) to get \( x^5 - x^2 \).
-
Subtraction: Subtract \( x^5 - x^2 \) from \( x^5 + 1 \). Since there are no other terms with \( x^5 \), this just eliminates the \( x^5 \) term, leaving \( x^2 + 1 \).
-
Bring Down Next Term: Since there are no \( x^4 \) or \( x^3 \) terms in the original dividend, we treat them as zero and continue with the subtraction result, \( x^2 + 1 \).
The result \( x^2 + 1 \) has a lower degree than the divisor \( x^3 - 1 \), so this concludes the division.
Thus, the quotient is \( x^2 \) and the remainder is \( x^2 + 1 \). The division process shows that:
Synthetic Method of division of Polynomials:
This is faster and requires lesser numerical calculations than long division method. Also instead of subtractions we are only dealing with the addition, so synthetic division is less prone to sign errors.
We can have two cases based on whether the divisor is a monic polynomial or not.
-
Divisor is a monic polynomial.
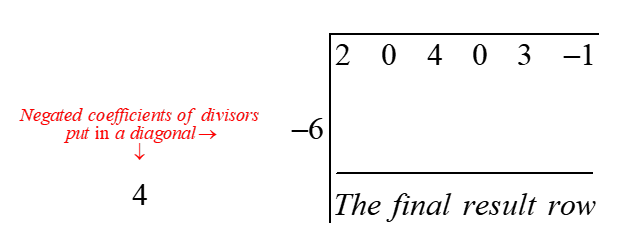
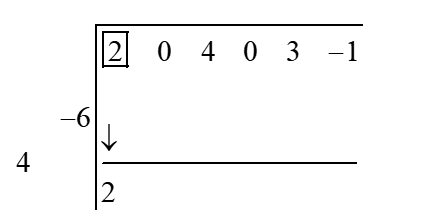
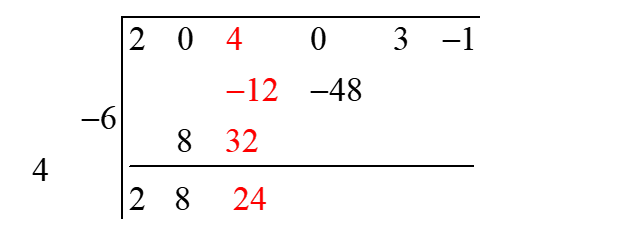
Let us explain this method with an example. Suppose we want to divide \(2x^5 + 4x^3 + 3x - 1\) by \(x^2 - 4x + 6\).
Step 1: Put the terms of divisor and dividend in descending order of degrees. The missing terms are replaced by terms having zero coefficients. Multiply the divisor with -1 (Negate all coefficients of divisor)
\[ -1(x^2 - 4x + 6) = -x^2 + 4x - 6 \]Step 2: Neglect the leading coefficient and put the rest of coefficient in diagonal (let us call this diagonal the "divisor diagonal") as shown in the example. Also put the coefficients of dividend in a row (let us call this row as "dividend row") as shown in the example.
Step 3: Leave the space of number of rows equal to the number of elements in divisor diagonal(which is equal to degree of divisor) Copy down the first element of dividend row directly to the final result row.
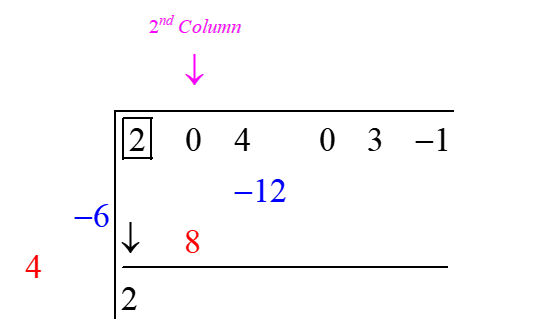
Step 4: Now multiply the first element of final result row with the elements of divisor diagonal row. You will obtain a diagonal whose lower left most element is in the second column of dividend coefficients.
Step 5: Add the elements of second column and put the sum in result row.
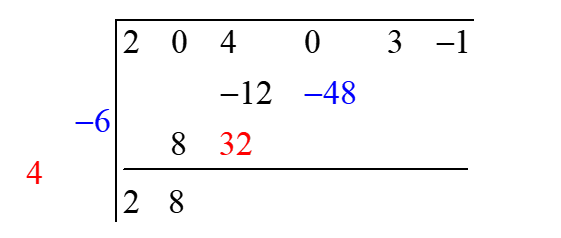
Step 6: Multiply the second element of the final result row to the divisor diagonal and put the obtained diagonal below dividend row that lower left most element now is in the third column.
Step 7: Now add the elements of the third column.
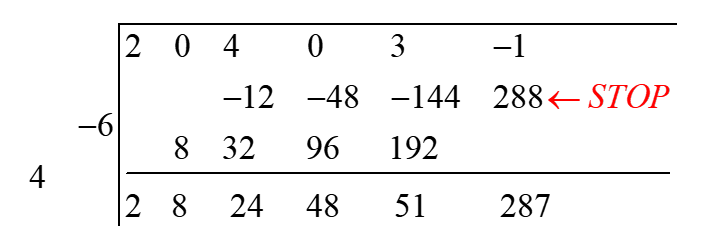
Step 8: Now continue with this process in Step 6 and Step 7. Stop as soon as the last column is filled with upper right most element of diagonal and add the last column elements to get the last element of the final result row.
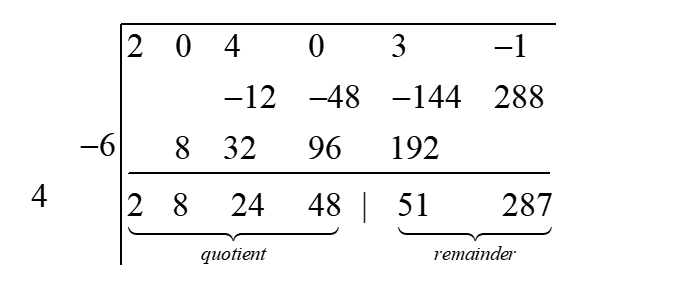
Step 9: If the degree of the divisor is \(n\) , then the last \(n\) elements of the final result row are the coefficients of the remainder and the remaining elements are the coefficients of the quotient.
So in the example the remainder is finally \( 51x + 287 \) and the quotient is \( 2x^3 + 8x^2 + 24x + 48 \). Thus,
\[ \frac{2x^5 + 4x^3 + 3x - 1}{x^2 - 4x + 6} = 2x^3 + 8x^2 + 24x + 48 + \frac{51x + 287}{x^2 - 4x + 6} \]Let us take more examples which will make process clearer.
Example
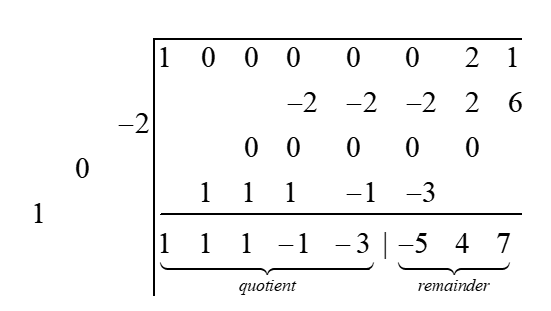
Divide \( x^7 + 2x + 1 \) by \( x^3 - x^2 + 2 \)
Solution: Multiply the divisor by -1. We get \( -x^3 + x^2 - 2 = -x^3 + 0.x^2 + x - 2 \)
Fill the table:
Therefore remainder\( = -5x^2 + 4x + 7 \) and quotient\( = x^4 + x^3 + x^2 - x - 3 \)
Thus,
\[ \frac{x^7 + 2x + 1}{x^3 - x^2 + 2} = x^4 + x^3 + x^2 - x - 3 + \frac{-5x^2 + 4x + 7}{x^3 - x^2 + 2} \] -
Divisor is a non-monic polynomial
When the divisor is a non-monic polynomial the synthetic division is modified a little bit. We first take the leading coefficient of divisor, let’s say \( k \), and what is left is a monic polynomial. We divide the dividend with this monic polynomial with the usual method. We obtain the quotient \( q(x) \) and \( r(x) \).
Then \( \frac{q(x)}{k} \) is the required quotient and \( r(x) \) is the remainder (remainder is the same).
Why?
Suppose we want to divide polynomial \( p(x) \) by non-monic polynomial \( d(x) \). Let us make \( d(x) \) monic by taking the leading coefficient \( k \) common. Let’s say that the new monic divisor is \( d'(x) = \frac{d(x)}{k} \). Then by Euclid’s Division Lemma, when we divide \( p(x) \) by \( d'(x) \), there exists polynomials \( q(x) \) and \( r(x) \) such that
\[ p(x) = q(x)d'(x) + r(x) \quad .....[1] \]Suppose we rewrite [1] as
\[ p(x) = \left( \frac{q(x)}{k} \right)(kd'(x)) + r(x) \quad .....[2] \]Which is same as \( p(x) = \left( \frac{q(x)}{k} \right)d(x) + r(x) \) (Since, \( d(x) = kd'(x) \)) .....[3]
Now [3] says that if we divide \( p(x) \) by \( d(x) \) then the quotient is \( \frac{q(x)}{k} \) and the remainder is \( r(x) \).
We may thus write the following theorem:
"When a polynomial \( P(x) \) is divided by a non-zero polynomial \( d(x) \) if \( q(x) \) is the quotient and \( r(x) \) is the remainder, then when \( P(x) \) is divided by \( kd(x) \), the remainder remains \( r(x) \) but the quotient becomes \( \frac{q(x)}{k} \)."